POI2015

KUR

首先设$z=ai+b$，考虑求出$z$的范围。假设序列的第$j$位为$1$，则$z+a(j-1)\geq p$，即将$[p,n)$区间向左循环位移$a(j-1)$，然后对所有这样的区间取交。

由于循环位移可能一个区间变成两个，因此直接取交不好做。考虑取反变成取并，然后排序即可。

但是你会发现样例过不去，观察一下发现最后$m-1$个即使合法也无法造成贡献，则暴力KMP即可。时间复杂度$O(m\log m)$

submission

TRZ

牛逼题，本来还口胡了一个$O(n\log n)$的诡异做法。

结论大概是左端点在前三个，或右端点在后三个。

考虑反证，也即证明左右都有三个不合法。设三个大小递减的字母依次为$A,B,C$。

首先证明不能有$A$，第一个位置显然不能，第二个位置如果是$A$，则第一个位置只能是$C$，考虑另外一边的第一个位置，如果是$B$则全部加一，矛盾。如果是$C$则$C$填了$A$的位置，矛盾。

第三个位置如果是$A$，则前两个不能都是$B$，而若$BC$均有也矛盾，若都为$C$则$C$填了$A$的位置。

因此不能有$A$。然后类似讨论也可以证明只有$BC$不合法，因此得证。

submission

MOD

首先维护树上最远点对，求出$f_{1,i}$表示一个点子树内最远点对，$f_{2,i}$表示一个点子树外最远点对。

然后最远的显然是选一条边断掉然后把两个直径接起来，最近的是一条边断掉然后两个直径中点接起来。

用树剖不要用欧拉序，会被卡空间。

submission

POD

和PKUSC2022D2T2差不多，对每种颜色随机哈希值，满足异或和为$0$，则颜色在同一边可以看作异或和为$0$，概率是$2^{-64}$。然后第二问双指针即可。

submission

KWA

是那种需要打打表才能知道的题捏。

首先显然$\frac{n(n+1)(2n+1)}{6}$处的答案为$n$，且是最后一个。打表发现最前面的$n+1$答案在$n$足够大时在$\frac{n(n+1)(2n+1)}{6}-128$处，足够大指$n^2>128$量级。

然后考察$[\frac{n(n+1)(2n+1)}{6}-128,\frac{n(n+1)(2n+1)}{6}]$内的所有$k(n)$，我们发现恰好和$[1,128]$内能否被组成出来相同。也即如果$j$不能被组成出来，则$\frac{n(n+1)(2n+1)}{6}-j$为$n+1$，否则为$n$。

这启发我们去证明，$\frac{n(n+1)(2n+1)}{6}-j$是由$1$到$n^2$减去某些$128$以内的平方数得到的。

考虑归纳。已知$n\leq 2870$内打表证明正确，往后的$n>400$，则上述范围只能由前面的$128$范围内加上$n^2$得到，也就可以得到这个循环。

则找个循环节就很好做了，时间复杂度$O(\log n)$但是我懒写了$O(\sqrt[3] n)$

submission

WYC

拆点，倍增，矩阵乘法。没了。

submission

LAS

首先有一个观察，如果有$2A_{i}<A_{i+1}$，则$i$一定会选择$i+1$，不论$i+1$是否选择$i+1$，对于$A_i>2A_{i+1}$同理。

则先把这样的人方向定出来，注意到可能有某个人选了以后他相邻的人也会定出方向，则需要BFS。

然后对于剩下的人，选最大的一定是合法的。因为不存在别人选了还能选的情况，所以不论他前面的人选了没有，他选最大的肯定不会反悔。

时间复杂度$O(n)$。

submission

CZA

首先这个问题可以转化成从小到大加入数，维护数形成的联通块的信息。

首先考虑$k=0$的情况，可以发现如果一个联通块的端点不为$[i-p,i-1]$范围内的数，那么这个端点就接不上去了，因此联通块的两端点必须都在$[i-p,i-1]$范围内。

再考虑加上这些限制，我们无非需要知道这些端点哪个是什么，则可以将这些也加入信息中。

对于$p\leq 3$的状态，这个信息不会很多，讨论以后总共$15$种，可以见下图。

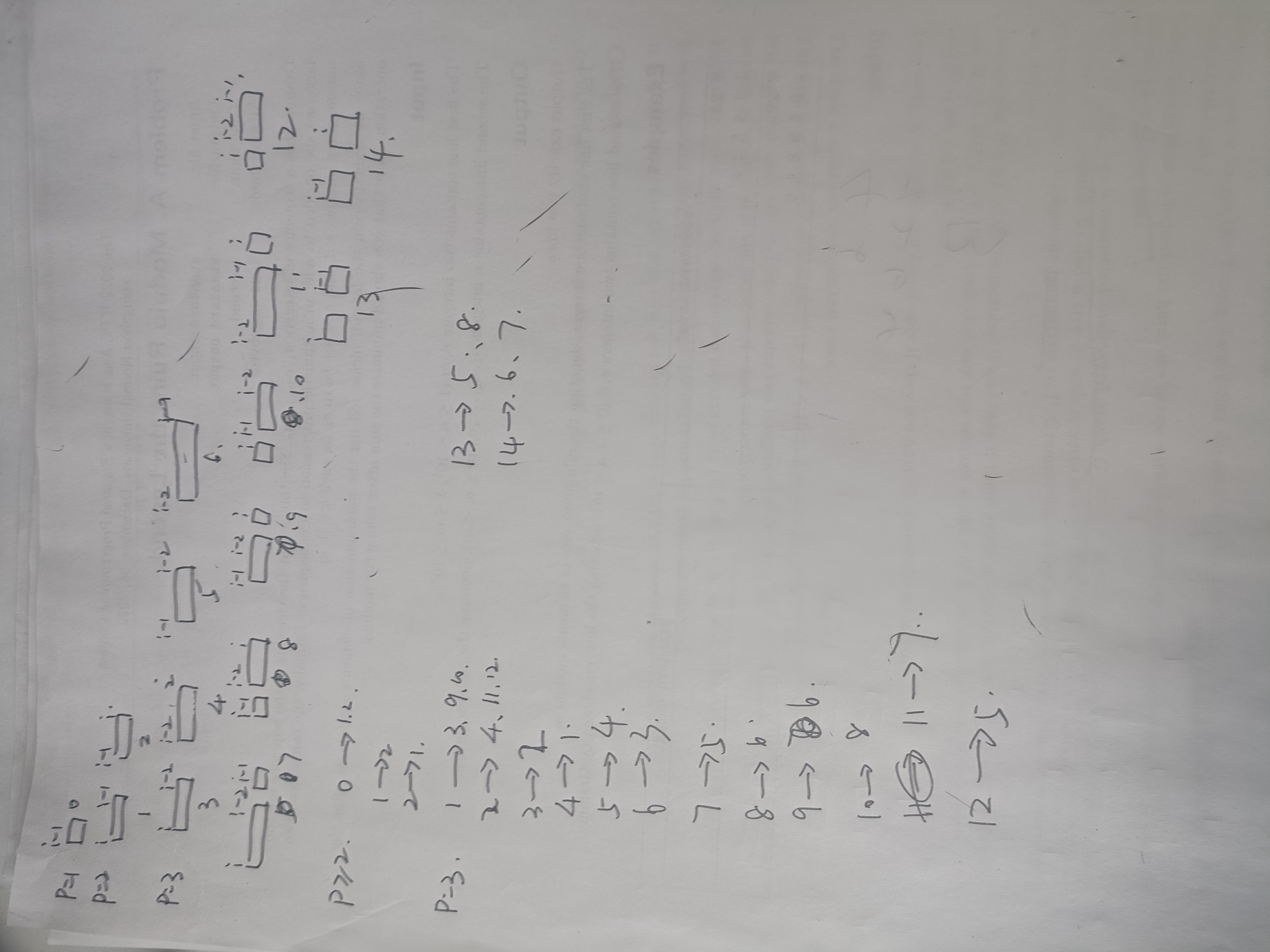
然后写个dp转移就好了。时间复杂度$O(n\operatorname{poly}(p))$

submission