DS博客作业03--树
0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结树及串内容
1.1.1串的BF\KMP算法
1.1.1.1BF算法
算法介绍
- 若现在两个字符串S和T,若要在S串中寻找T串,则S串称为目标串,T串成为模式串。
- 取T的第一个字符和S的第一个字符比较,若匹配则再取S的第二个字符和T的第二个字符比较,若不匹配则取S的第二个字符和T的第一个字符从头比较,以此类推,直到在T中完整匹配出S串。
- 该算法时间复杂度时间复杂度较高,最坏的情况可达O(m*n)(m,n分别为S和T的字符串长度),因此此算法又称蛮力算法。
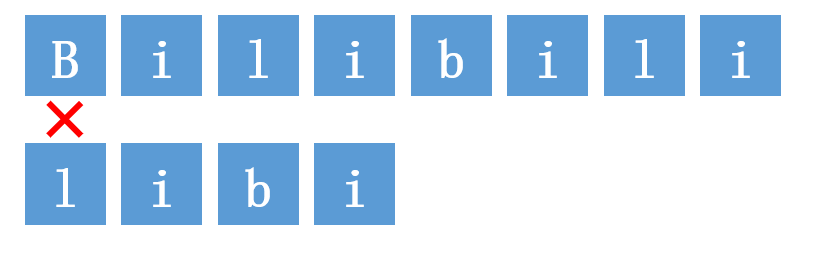
图示助通
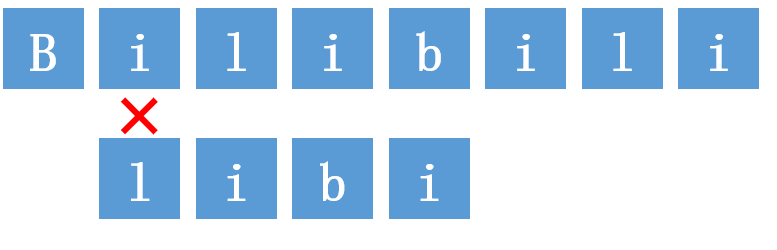
1.目标串S的第一位开始与模式串T第一位匹配,B与l不匹配,匹配失败
![]()
2.目标串S第二位开始与模式串T第一位匹配,i与l不匹配,匹配失败
![]()
3.目标串S第三位开始与模式串T第一位匹配,S与T四个字母全部匹配,匹配成功
![]()
代码实现
int StrCompare_BF(string S, string T, int pos = 0)
{
int i = pos; //i用于主串S的起始位置
int j = 0; //子串的起始位置
int lenS = S.size();
int lenT = T.size();
while (i < lenS&&j < lenT)
{
if (S[i] == T[j])
{
++i;
++j;
}
else
{
//当字符不匹配的时候,i回溯,移动到下一位
i = i - j + 1;
j = 0;
}
}
if (j >= lenT)
{
return i - j; //匹配成功则返回T在S串中出现的第一个位置
}
else
{
return -1; //未成功
}
}
1.1.1.2KMP算法
算法介绍
步骤图解
1.1.2二叉树相关梳理
1.1.2.1存储结构
顺序表存储(数组)
-
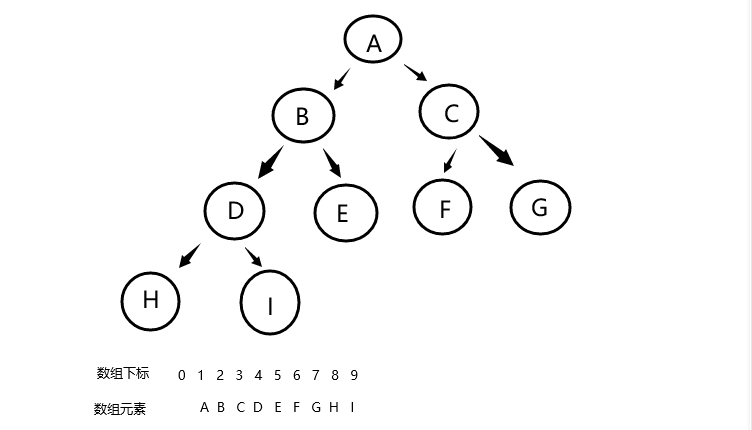
图示助通(完全二叉树和非完全二叉树)
![]()
![]()
-
说明
顺序存储就是创建一个数组来存放树结点(注意到数组的第一个空间是舍弃不用的),依次从下标1开始按第一层,第二层,第三层的顺序逐个存储结点数据,那么我们由上面两种树的存储情况来看,完全二叉树用数组来存储是较为合理的,但不完全二叉树用数组来存放会浪费很多空间,如果在此时树的深度很大很大,那么浪费的空间是难以想象的,此时更适合用二叉链来存放,由下面介绍。
二叉链表存储
结构体定义
typedef struct BTNode
{
int data;
struct BTNode* lchild; //结点数据域
struct BTNode* rchild; //左右孩子指针
}BTNode,*BiTree;
图示助通(以上面非完全二叉树为例)
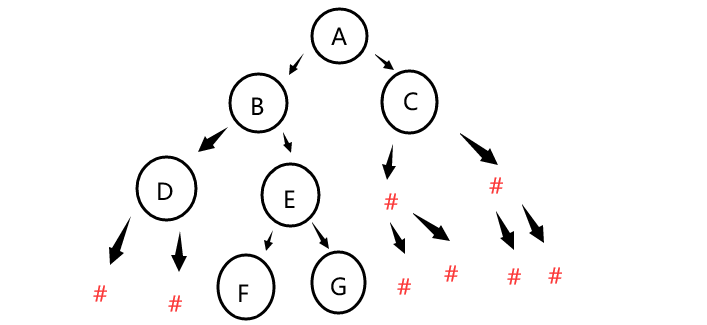
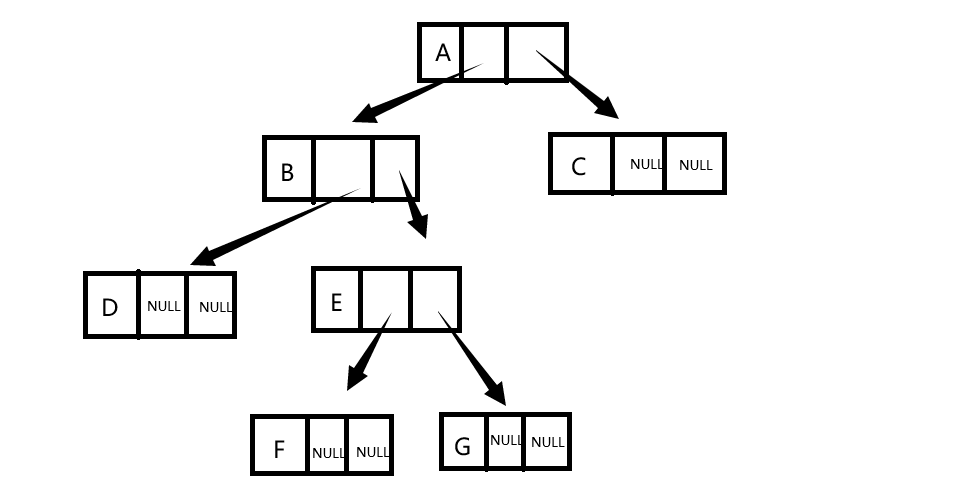
1.1.2.2建法
根据其先序遍历递归
- 法一:函数无返回
void CreateTree(BiTree& T, string str, int &i) //i是引用变量,值的改变是全局的
{
int len = str.size();
if ( i >= len) //必须先判断str的遍历是否到头,否则会出现越界访问
{
T = NULL;
return;
}
if (str[i] == '#')
{
T = NULL;
return;
}
T = new BiTNode;
T->data = str[i];
CreateTree(T->lchild, str, ++i);
CreateTree(T->rchild, str, ++i);
}
- 法二:函数返回根结点
BiTree CreateTree(string str, int &i)
{
BiTree T;
int len = str.size();
if ( i >= len)
{
return NULL;
}
if (str[i] == '#')
{
return NULL;
}
T = new BiTNode;
T->data = str[i];
T->lchild=CreateTree( str, ++i);
T->rchild=CreateTree( str, ++i);
}
根据其顺序存储(层次)结构
-
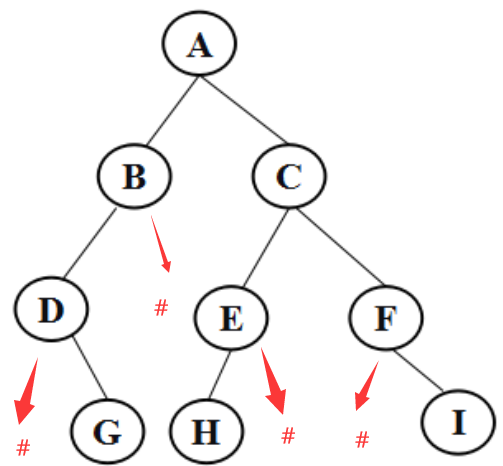
首先将树的空结点补齐
![]()
-
再用数组来层次存储
ABCD#EF#GH##I######(可理解为层次存储,#代表空结点) -
代码
BiTree CreateTree(string str, int &i)
{
BiTree T;
int len = str.size();
if ( i >= len)
{
return NULL;
}
if (str[i] == '#')
{
return NULL;
}
T = new BiTNode;
T->data = str[i];
T->lchild=CreateTree( str, i*2); //与先序建树的区别
T->rchild=CreateTree( str, i*2+1);
}
根据先,中序还原树
-
图示
-
具体代码
BTree CreateTree(char *pre,char *in,int n) //pre和in是分别指向先序字符串和中序字符串第一个字符的指针
{
BTNode *s;
char *op;
int k;
if(n<=0)
{
return NULL;
}
s=new BTNode;
s->data=*pre;
for(op=in;p<in+n;p++) //在中序序列中寻找根结点
{
if(*op==*pre)
{
break;
}
}
k=op-in;
s->lchild=CreateTree(pre+1,in,k); //递归往下生成结点
s->lchild=CreateTree(pre++k+1,op+1,n-k-1);
return s;
}
根据中,后续还原树
- 图示
- 具体代码
BTree CreateTree(char *post,char *in,int n) //post和in是分别指向先序字符串和中序字符串第一个字符的指针
{
BTNode *s;
char *op;
int k;
if(n<=0)
{
return NULL;
}
s=new BTNode;
s->data=*(post+n-1);
for(op=in;p<in+n;p++) //在中序序列中寻找根结点
{
if(*op==*(post+n-1)
{
break;
}
}
k=op-in;
s->lchild=CreateTree(post,in,k); //递归构造左右子树
s->lchild=CreateTree(post+k,op+1,n-k-1);
return s;
}
1.1.2.3遍历(递归遍历和层次遍历)
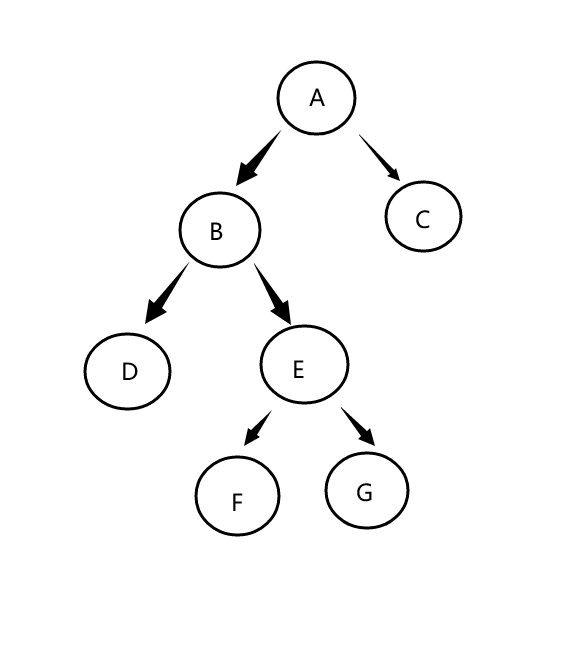
以此二叉树为例
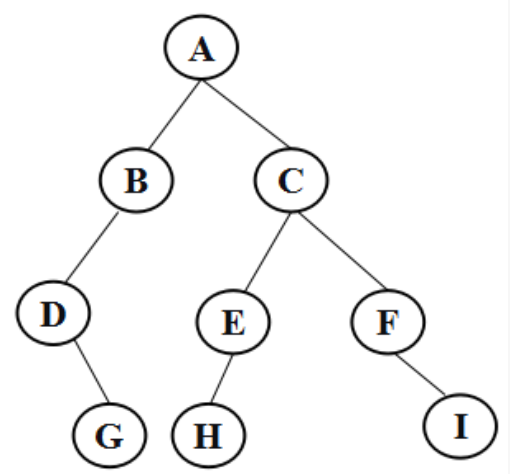
递归遍历
- 先序
遍历结果:ABDGCEHFI
代码
void PreOrder(BTree T)
{
if(T==NULL)
{
return; //递归口退出递归
}
else
{
cout<<T->data;
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
- 中序
遍历结果:DGBAHECFI
代码
void InOrder(BTree T)
{
if(T==NULL)
{
return; //递归口退出递归
}
else
{
InOrder(T->lchild);
cout<<T->data;
InOrder(T->rchild);
}
}
- 后序
遍历结果:GDBHEIFCA
代码
void PostOrder(BTree T)
{
if(T==NULL)
{
return; //递归口退出递归
}
else
{
PostOrder(T->lchild);
PostOrder(T->rchild);
cout<<T->data;
}
}
层次遍历
遍历结果:ABCDEFGHI
思路图解:
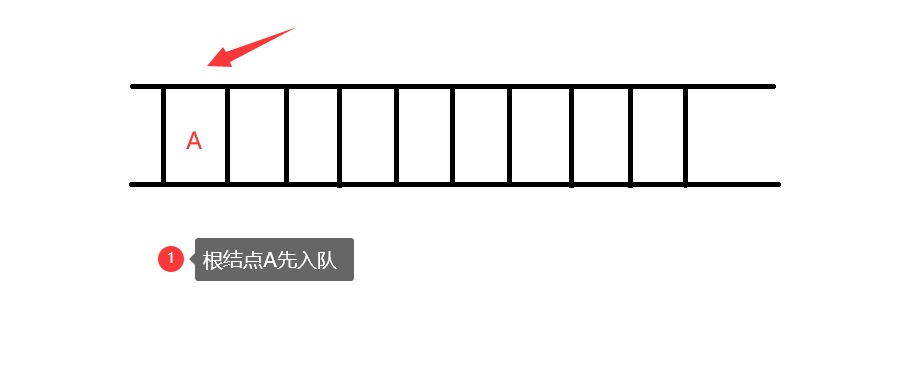
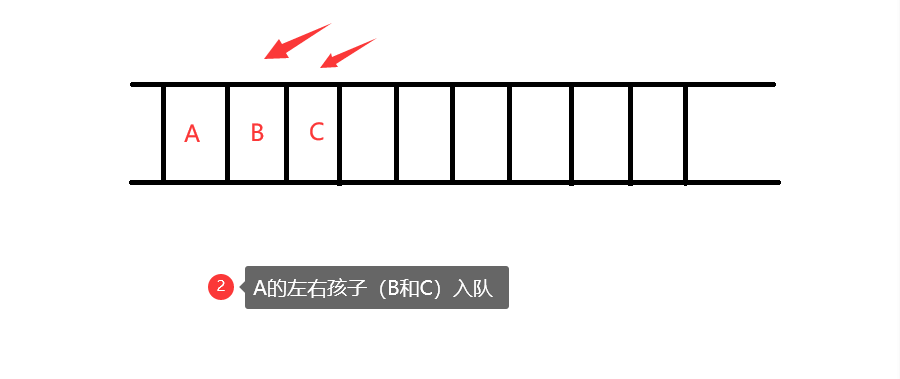
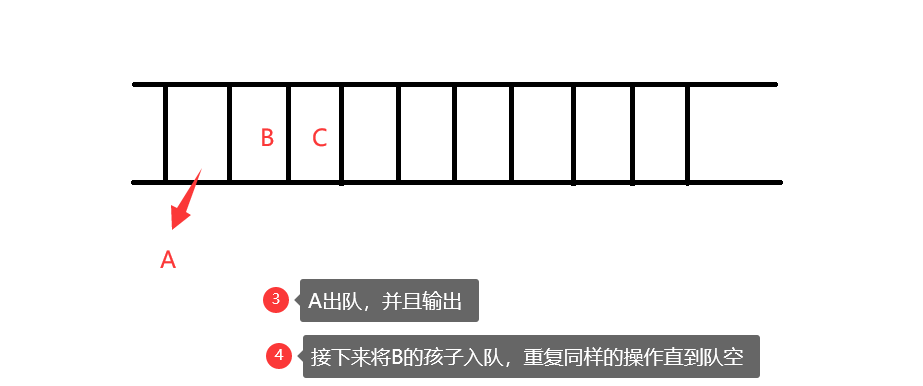
代码
void LevelOrder(BTree T)
{
queue<BTree>Q;
BTree Temp;
if(T!=NULL) //先将根结点入队
{
Q.push(T);
}
else
{
return;
}
while(!Q.empty())
{
Temp=Q.front();
if(Temp->child!=NULL)
{
Q.push(Temp->child);
}
if(Temp->lchild!=NULL)
{
Q.push(Temp->lchild);
}
cout<<Temp->data;
Q.pop();
}
}
总结:先,中,后序遍历二叉树的区别仅仅在于输出结点先后顺序的控制,所以整合为递归遍历,与层次遍历区别开来。
1.1.2.4应用
1.1.3树的相关梳理
1.1.3.1树的结构
双亲表示法
- 结构体定义
typedef struct PTNode
{
ElemType data;
int parent; //指向双亲的下标
}PTNode; //结点结构体
typedef struct
{
PTNode nodes[MAXSIZE];
int root; //指向根结点的下标
int count; //结点数
}PTree;
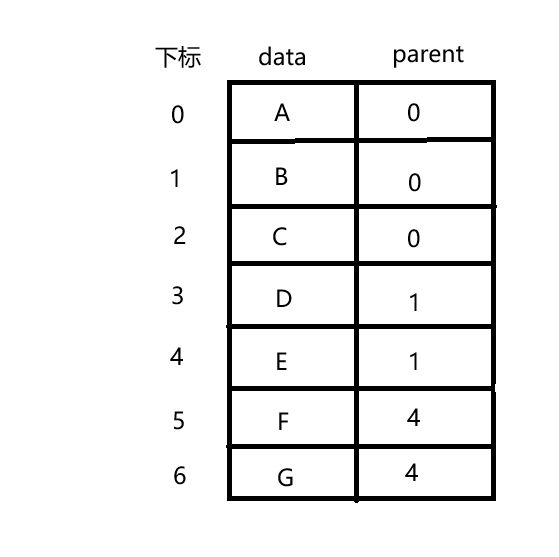
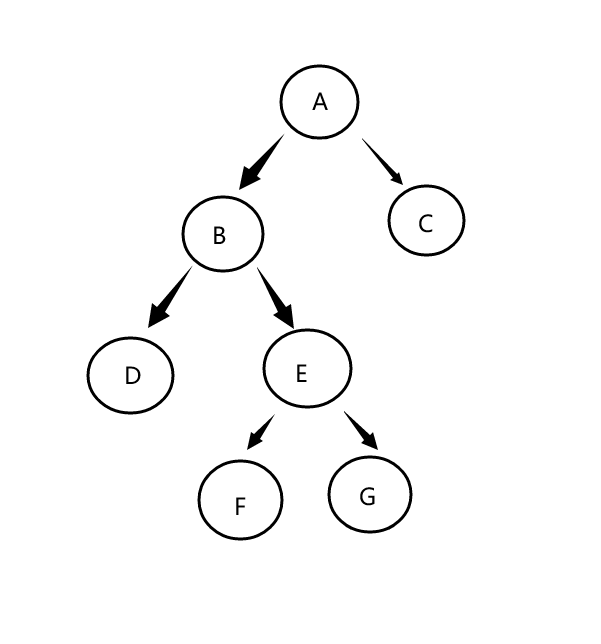
- 概念理解:
1.采用顺序表(数组)存储各个结点。
2.给各个结点附上一个变量parent,用来记录双亲在数组中的下标 - 图示助通:
![]()
![]()
孩子表示法
- 结构体定义:
typedef struct CTNode
{
int child; //指向第一个孩子
struct CTNode *next; //指向后续孩子
}*ChildPtr;
typedef struct
{
ElemType data;
ChildPtr *firstchild; //指向第一个孩子
}CTBox; //定义表头结构体
typedef struct
{
PTNode nodes[MaxSize]; //存储结点
int root; //指向根结点的下标
int count; //结点数
}CTree; //定义树结构体
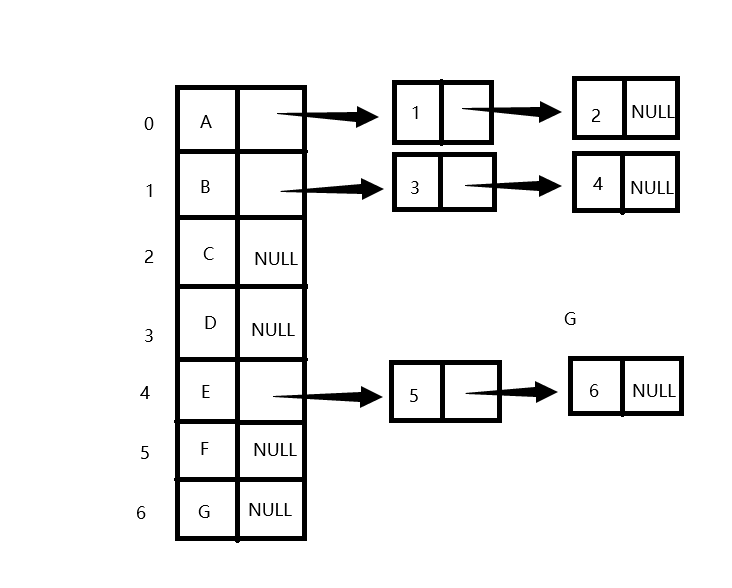
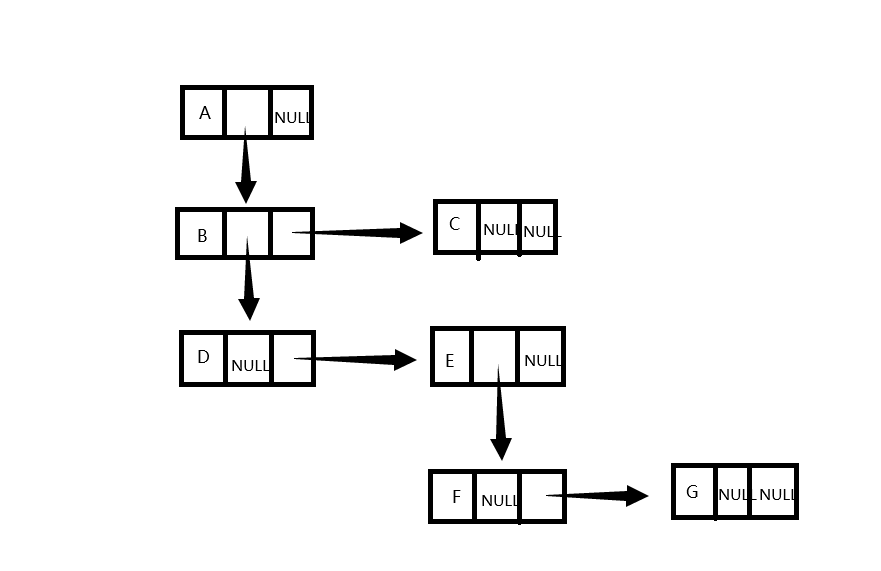
- 概念理解:
1.存储树采用的是 "顺序表+链表" 的组合结构
2.从根结点开始,由数组存储各个结点。
3.给各个结点分配一个链表,若有孩子,则链表节点存孩子在数组中的下标,下一个链表节点是第二个孩子,以此类推;若无孩子,则该链表就是NULL。 - 图示助通:
![]()
孩子兄弟表示法
- 结构体定义:
#define ElemType char
typedef struct CSNode{
ElemType data;
struct CSNode * firstchild,*nextsibling; //指向第一个孩子和指向相邻的兄弟
}CSNode,*CSTree;
- 概念理解:
1.采用的是链式存储结构。
2.结构体成员有data(数据域),nextbro(指向双亲相同的兄弟结点),firstchild(指向第一个孩子结点) - 图示助记
![]()
![]()
1.1.4线索二叉树
1.1.4.1线索树的注意点
- 空的左孩子指针指向该结点的前驱;空的右孩子指针指向该结点的后继。这种附加的指针值称为线索,带线索的二叉树称为线索二叉树。
- 为了标志左右孩子指针的空与不空,在结构体定义中增加了两位成员ltag,rtag,若左孩子指针为空,则ltag值赋为1,不空则为0。
- 在不同的遍历次序下,二叉树中的每个结点一般有不同的前驱和后继。因此,线索二叉树又分为前序线索二叉树、中序线索二叉树和后序线索二叉树3种
1.1.4.2线索树的结构体定义
typedef struct BTNode
{
struct BTNode* lchild,rchild;
int ltag,rtag;
}
1.1.4.3举例(先序,中序,后序)
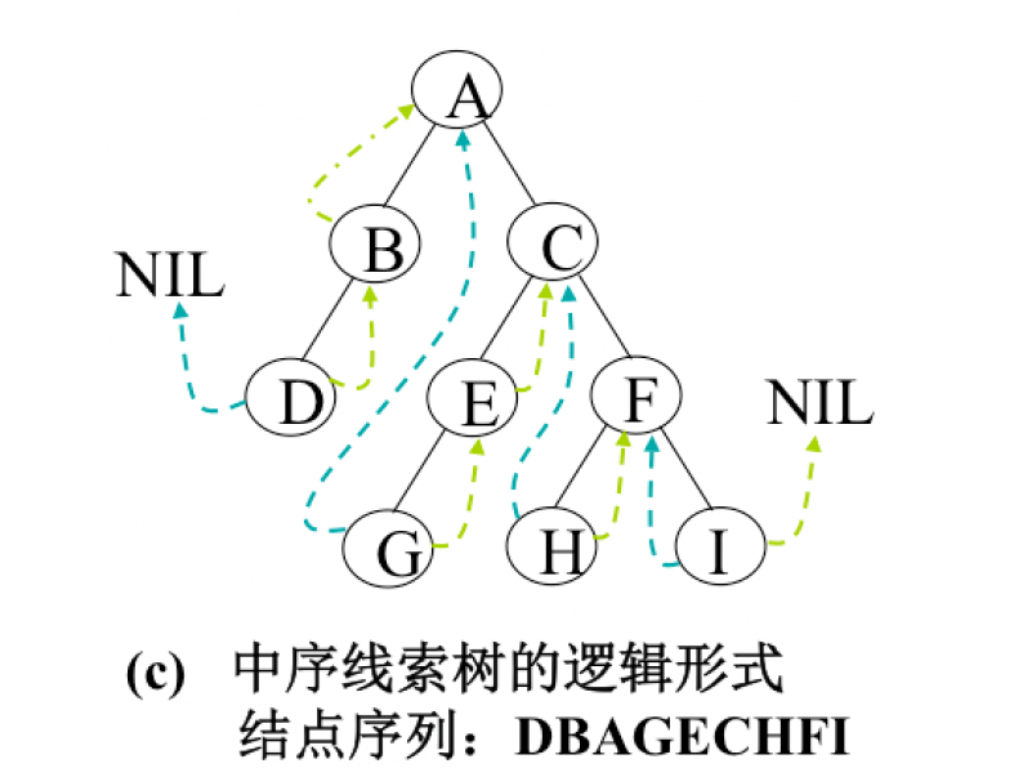
- 以中序为例
![]()
1.1.5数的特殊应用
1.1.5.1哈夫曼树
字符编码问题的提出
- 若有一段字符为abbaca,出于某种需求将其用二进制(0和1)编码
- 若分别表示为a(01),b(000),c(00),则字符串完整编码为01000000010001
- 问题便来了,若将第二步二进制编码解码为原字符,字符串acccaca也符合条件,那么如何使解码唯一呢
- 问题二:如何使解码唯一的同时,占用二进制为最少呢
问题的解决 - 为使得编码唯一,某个字符二进制编码的后缀不能为另一个字符的前缀,发现用二叉树的叶子结点表示这些字符,从根结点开始,在寻找字符的过程中,往左走编码为0,右则为1。
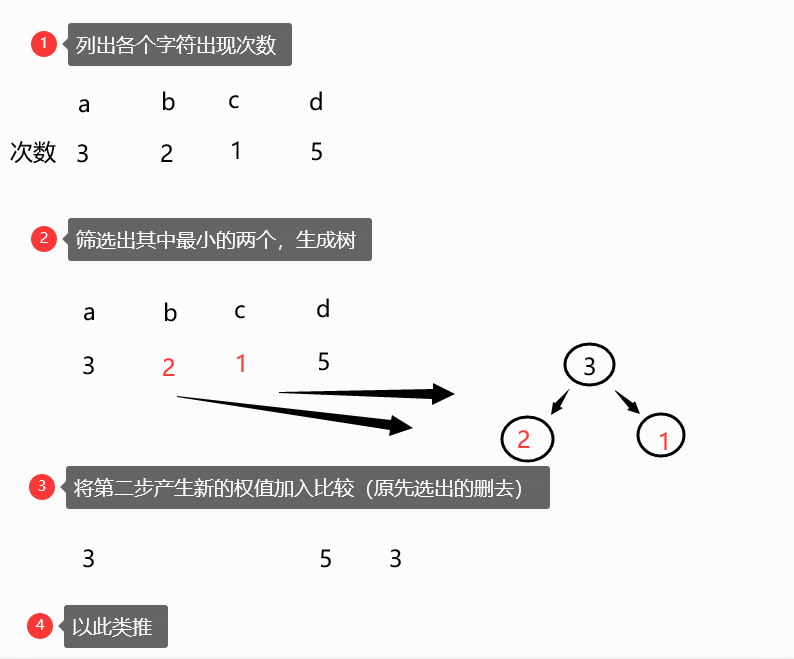
- 为使得编码长度最短,则在字符串中出现次数越少的字符所在层数应该越高,所以在建树过程中,字符出现的次数作为其权重,在所有权重中寻找最小的两个,组成一棵树,它们分别为叶子结点,根结点权重为它们权重的和,再将根结点的权重加入原来的比较中,直到最后只剩一个结点。
图示助通(字符串addbbaddcad为例)
![]()
![]()
1.1.5.2并查集
引例
1.2.学习体会
本章的树相较于上一章的栈和队列来说,我个人认为难度会稍大一点,因为树的多个操作和应用需要进行递归运算,这对于递归函数结构的设计和参数传递的精准度要求较高,将考验我们的抽象思维和逻辑思维,此时若感觉到困难,可借助手动步骤演示来帮助函数设计。那么对于学好树的内容来说,除了上面的建议之外,我们还应该要熟记许多小知识和基操:概念如满二叉树,完全二叉树,树的高度,度,完全二叉树的叶子结点个数计算,基操如三序遍历,层次遍历,算数高度,层数,wpl。
2.阅读代码(0--5分)
找4份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
考研题
PAT\天梯赛题目
ACM题解
leecode--树
注意:不能选教师布置在PTA的题目。完成内容如下。
2.1 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。题目截图后一定要清晰。
2.1.1 该题的设计思路
链表题目,请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。
2.1.2 该题的伪代码
文字+代码简要介绍本题思路
2.1.3 运行结果
网上题解给的答案不一定能跑,请把代码复制自己运行完成,并截图。
2.1.4分析该题目解题优势及难点。
评分注意
本学期,博客作业重点会在知识总结及代码阅读内容。代码阅读部分务必按照要求详细介绍解题思路。回答简单应付,博客书写没有看出作者对代码理解,则得0分。
------------恢复内容结束------------
*------------恢复内容结束------------






 浙公网安备 33010602011771号
浙公网安备 33010602011771号