矩阵分解

给出一些用户对电影的打分信息

	电影1	电影2	电影3	电影4
用户1	1	4	5	未打分
用户2	5	5	4	未打分
用户3	4	3	未打分	5
用户4	未打分	5	2	未打分
用户5	3	未打分	4	3

如何通过已知的打分信息估算出表格中未打分的实际分数，可以将这个表格看作是一个矩阵，采用矩阵分解的方法进行解决。

设当前矩阵为R（n,m),R(n,m)可以分解为为两个矩阵P(n,K)和Q(n,k)的乘积，这里需要了解矩阵乘法的相关知识.矩阵P(n,K)表示n个用户和K个特征之间的关系矩阵，这K个特征是一个中间变量，矩阵Q(K,m)的转置是矩阵Q(m,K)，矩阵Q(m,K)表示m个i电影和K个特征之间的关系矩阵。

然后构造损失函数，损失函数的构造有很多方法。一般采用平方构造法，即使用原始的矩阵与重新构建的矩阵之间的误差的平方作为损失函数。如果R(i,j)已知，则R(i,j)的误差平方和为：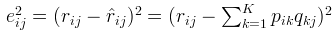

最终，需要求解所有的非“-”项的损失之和的最小值：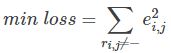

然后 使用梯度下降法获得修正的p和q分量：

     

     

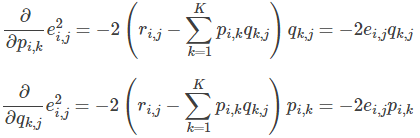
 然后 不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）

 为了防止过度拟合常常增加正则项，方法同上，只是在损失函数后增加正则项