5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

机器学习主要分为这四大类：

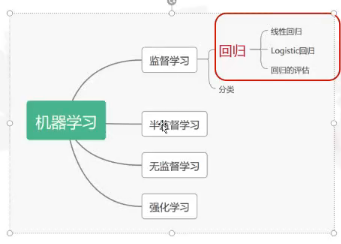
回归与分类的区别：

线性回归定义：通过一个或者多个自变量与因变量之间进行建模的回归方法，其中可以为一个或者多个自变量之间的线性组合。

回归预测其实就是找到一个权重乘与特征值再加上回归系数。y=w*x+b

1.线性回归就是通过自己获取的数据，预测出其他的数据。
误差(损失函数):预测出来的值会存在一些误差，但总的来说接近现实。
回归:线性回归，逻辑斯特回归，回归的评估。

机器预测与真实值是有一定的误差的，我们能够尽可能的减小误差，所以就有了损失函数（误差的大小）。

 

 

最小二乘法之梯度下降：通过训练次数的增加，不断下降，预测值会越来越接近于真实值。

 

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

虽说股票这个东西波动因素有很多，但是还是可以通过几年之内的数据，以及某些波动因素进行一定的预测的。还有天气等。

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

源代码：

#根据y=2*x+b随意写几个数
X=[1,2,3,4,5,6,7]
Y=[3.09,5.06,7.03,9.12,10.96,12.91,15.01]
Xsum=0.0
X2sum=0.0
Ysum=0.0
XY=0.0
n=len(X)
for i in range(n):
    Xsum+=X[i]
    Ysum+=Y[i]
    XY+=X[i]*Y[i]
    X2sum+=X[i]**2
k=(Xsum*Ysum/n-XY)/(Xsum**2/n-X2sum)
b=(Ysum-k*Xsum)/n
print('the line is y=%f*x+%f' % (k,b) )

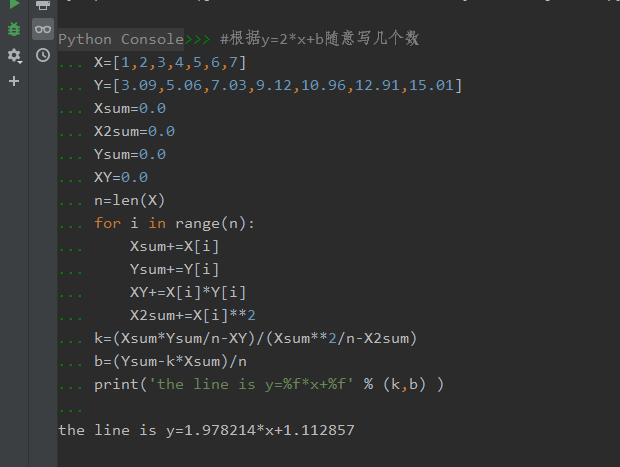
结果：