图总结
一、思维导图
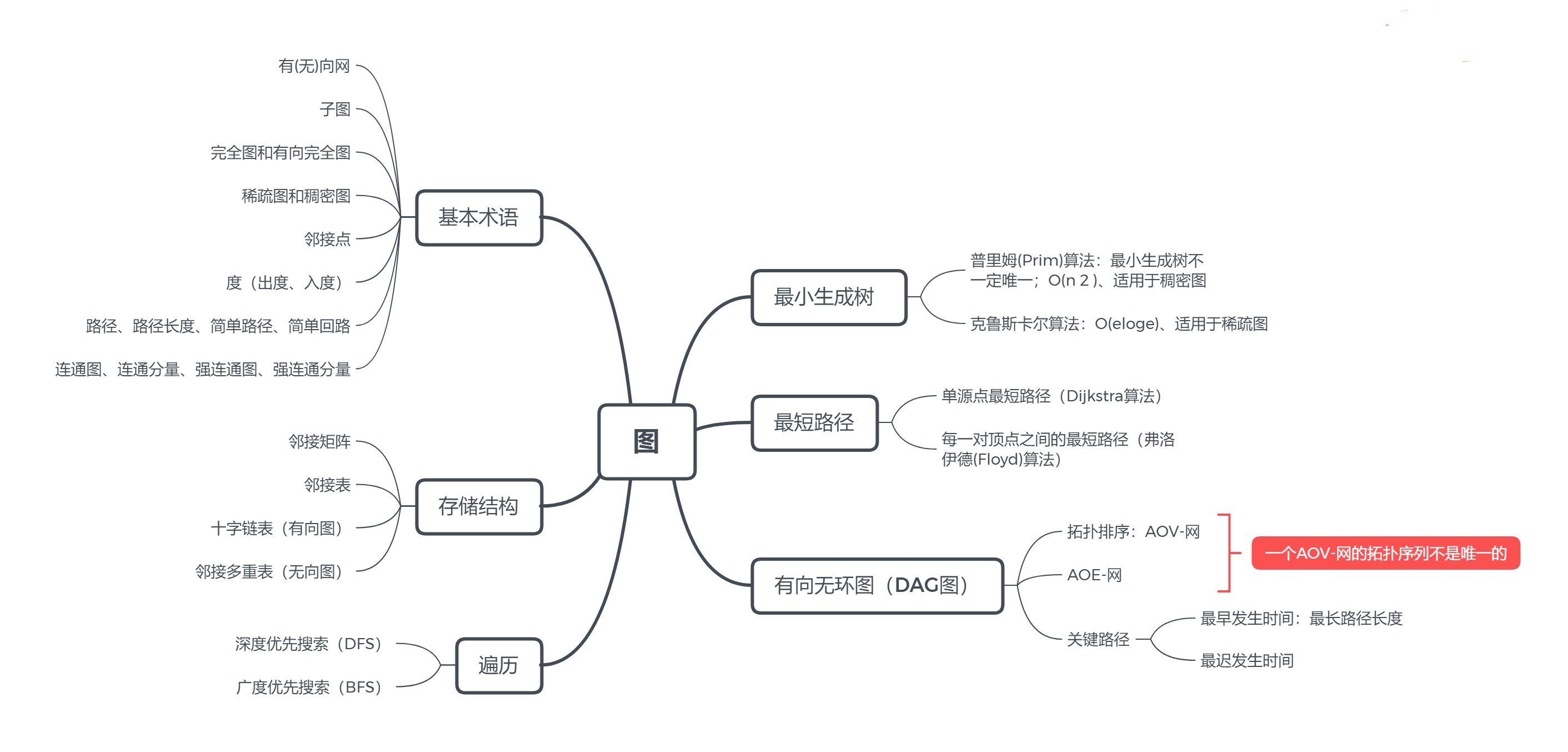
二、重要概念
1、基本术语
a、完全图
e=n(n-1)/2
b、有向完全图
e=n(n-1)
c、稀疏图和稠密图
若边或弧的个数 e<nlogn,则称作稀疏图,否则称 作稠密图
d、连通图
图G中任意两个顶点之间都有路径相通
e、强连通图
任意两个顶点之间都存在一条有向路径
2、存储结构
a、邻接矩阵
1)无向图的邻接矩阵是对称的,有向图的邻接矩阵可能是不对称的
2)C语言形式描述
#define MaxInt 32767 //表示极大值
#define MVNum 100 //最大顶点数
typedef char VerTexType; //假设定点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct { // 图的定义
VerTexType vexs[MVNum]; // 顶点表
ArcType arcs[MVNum][MVNum]; // 弧的信息(邻接矩阵)
int vexnum, arcnum; // 图当前的顶点数和边数
} AMGraph; //邻接矩阵
3)借助于邻接矩阵求得顶点的度
无向图:统计第i行(列)1的个数
有向图:统计第i行1的个数可得顶点i的出度;统计第j列1的个数可得顶点j的入度
b、邻接表
图的结构定义:
typedef struct {
AdjList vertices;
int vexnum, arcnum;
} ALGraph;
C语言类型描述:
表(弧/边)结点:adjvex+nextarc+info
typedef struct ArcNode {
int adjvex; // 该弧所指向的顶点的位置
struct ArcNode *nextarc;//指向下一条弧的指针
InfoType *info; // 该弧相关信息的指针
} ArcNode;
头结点:data+firstarc
typedef struct VNode {
VerTexType data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
} VNode, AdjList[MAX_VERTEX_NUM];
c、十字链表
将有向图的邻接表和逆邻接表结合起来的一种链表,从横向上看是邻接表,从纵向上看是逆邻接表
3、遍历:每个顶点仅被访问一次
a、 深度优先搜索:类似于树的先根遍历,利用栈
实质 :对每个顶点查找其邻接点的过程
b、广度优先搜索:利用队列
实质 :通过边或弧找邻接点的过程
4、最小生成树:权值之和最小
a、普里姆(Prim)算法:适用于稠密图
基本思想:第一步:取图中任意一个顶点 v 作为生成树的根;第二步:往生成树上添加新的顶点 w。在添加的顶点w 和已经在生成树上的顶点v 之间必定存在一条边,并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小;第三步:继续往生成树上添加顶点,直至生成树上含有 n 个顶点为止
注意:构造的最小生成树不一定唯一,但最小生成树的权值之和一定是相同的
b、克鲁斯卡尔算法:适用于稀疏图
基本思想:第一步:构造一个只含 n 个顶点的子图 SG;第二步:从权值最小的边开始,若它的添加不使SG中产生回路,则在 SG 上加上这条边;第三步:如此重复,直至加上 n-1 条边为止
5、最短路径
a、单源点最短路径
Dijkstra算法:初始时,令 S={V0 },T={其余顶点},T中顶点对应的距离值,若存在<V0 ,Vi>,距离值为<V0 ,Vi>弧上的权值,若不存在<V0 ,Vi>,距离值为∞;从T中选取一个其距离值为最小的顶点W, 加入S;对T中顶点的距离值进行修改:若加进W作中间顶点,从V0 到Vi的距离值比不加W的路径要短,则修改此距离值;重复上述步骤,直到S中包含所有顶点,即S=V为止
b、每一对顶点之间的最短路径
弗洛伊德(Floyd)算法:逐个顶点试探;从v i 到v j 的所有可能存在的路径中,选出一条长度最短的路径
6、有向无环图(DAG图)
a、拓扑排序:检查有向图中是否存在回路的方法之一
1)拓扑有序序列:按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系,由此所得顶点的线性序列称之为拓扑有序序列
2)AOV-网:用顶点表示活动,用弧表示活动间的优先关系的有向图称为顶点表示活动的网(Activity OnVertex Network),简称AOV-网
注意:在AOV-网中不应该出现有向环;对给定的AOV-网需首先判断网中是否有环;一个AOV-网的拓扑序列不是唯一的
拓扑排序的步骤: 从有向图中选取一个没有前驱的顶点,并输出之;从有向图中删去此顶点以及所有以它为尾的弧;重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止
c、关键路径和AOE-网
1)AOE-网:边表示活动的网
事件vi的最早发生时间:从开始点v1到vi的最长路径长度。用ve(i)表示
事件vi的最迟发生时间:在不推迟整个工期的前提下,事件vi允许的最晚发生时间。用vl(i)表示
2)关键路径的算法:求ve的顺序应该是按拓扑有序的次序;求vl的顺序应该是按拓扑逆序的次序;
⑴输入e条弧,建立AOE-网。
⑵从源点v 0 出发,令ve[0] = 0, 按拓扑有序求各顶点的最早发生时间vei,如果得到的拓扑序列中顶点个数小于网中顶点数n,说明网中存在环,不能求关键路径,算法终止;否则执行步骤
⑶从汇点v n 出发,令vl[n-1] = ve[n-1]; 按逆拓扑有序求其余各顶点的最迟发生时间vli;
⑷根据各个顶点的ve和vl值,求每条弧s的e(s)和l(s)。若某条弧满足e(s) == l(s),则为关键活动,由所有关键活动所连成的那一条路径就为关键路径
三、疑难问题及解决方案
1、如何求Dijkstra算法中的D[]andPath[]数组
数组D[]存放当前找到的从源点V 0 到每个终点的最短路径长度,其初态为图中直接路径权值;
数组path[]表示从V 0 到各终点的最短路径上,此顶点的前一顶点的序号;若从V 0 到某终点无路径,则用0作为其前一顶点的序号

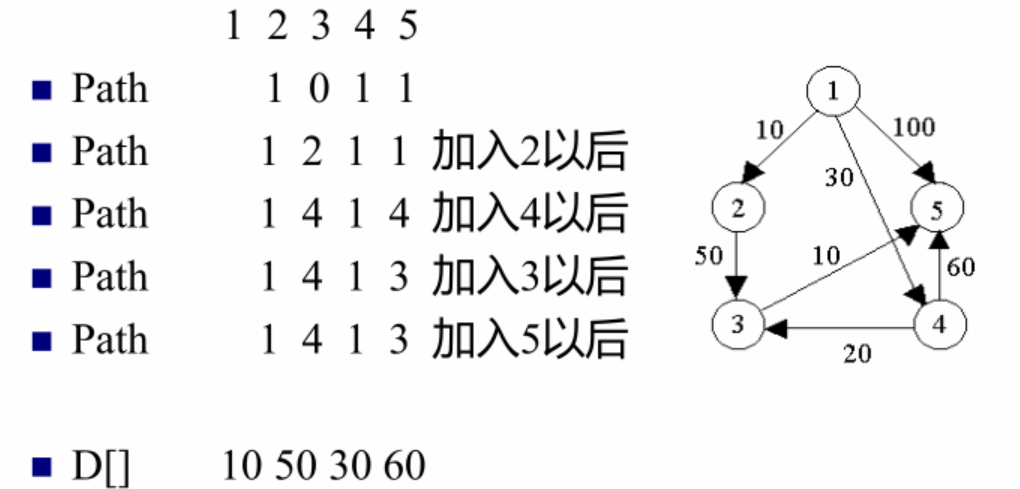
初始时,1可直接到达2、4、5,不能到达3,1到2、3、4、5的最短路径分别是10、无穷大、30、100,path[2]、path[4]、path[5]的值为源点1的序号,也就是1,而path[3]=0 ;加入2后,由于2可到达3,1到达3的最短路径变为10+50=60,小于无穷大,所以path[3]变为2的序号,也就是2,其他点的最短路径不变;加入4后,1到达3、5的最短路径发生变化,路径分别是1->4->3、1->4->5,最短路径变为50、90,到达3的前一顶点序号变为4,到达5的前一顶点序号变为4;加入3以后,1到达5的最短路径(1->2->3->5)变为10+50+10=70,小于90,所以path[5]变为3;加入5后,1到达其他点的最短路径都不变,所以path[]数组的值都不变,最终得到1到达2、3、4、5的最短路径分别是10、50、30、70




 浙公网安备 33010602011771号
浙公网安备 33010602011771号