树、二叉树、查找算法总结
一、思维导图
二、重要概念的笔记
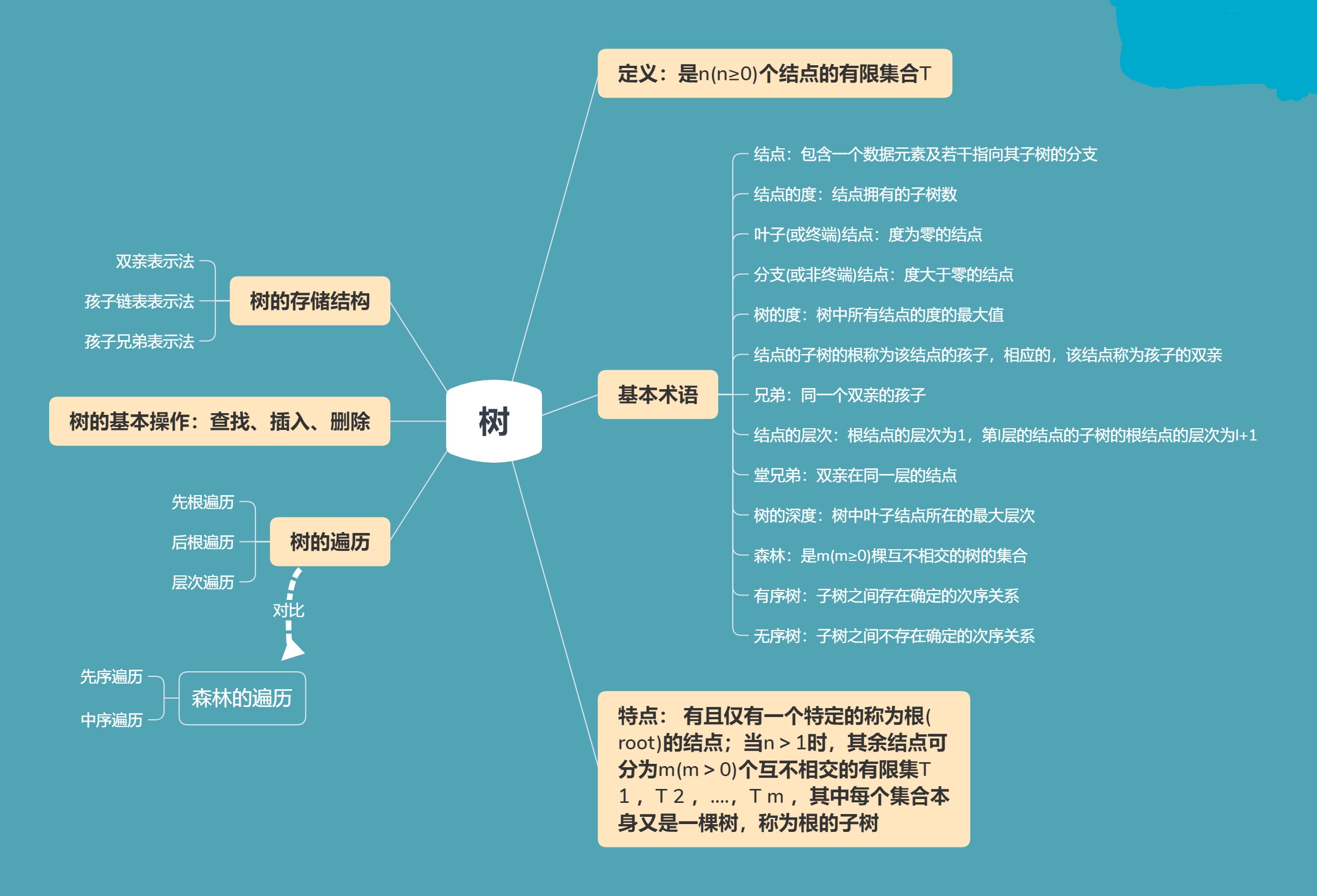
1、树
(1)树的遍历
a、层次遍历:从根结点开始,从上到下,从左到右,一层一层地访问每个结点
b、先根遍历:先访问根结点,再从左往右遍历根结点的子树
c、中根遍历:先从左往右遍历根结点的子树,再访问根结点
(2)树的存储结构
a、双亲表示法:用一组连续空间存储树的结点,并附设一个指示器指示其双亲结点的位置;适用于双亲的操作的实现
结构特点:data+parent
typedef struct PTNode {
Elem data;
int parent; // 双亲位置域
} PTNode;
树结构:
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int r, n; // 根结点的位置和结点个数
} PTree;
b、孩子链表表示法:定义两个表,即树结点表和孩子结点表;便于那些涉及孩子的操作的实现
孩子结点结构:child+next
typedef struct CTNode {
int child;
struct CTNode *next;
} *ChildPtr;
双亲结点特点:data+firstchild
typedef struct {
Elem data;
ChildPtr firstchild;
// 孩子链的头指针
} CTBox;
树结构:
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n, r;
// 结点数和根结点的位置
} CTree;
孩子-兄弟表示法:链表中结点的两个链域分别指向结点的第一个孩子结点和下一个兄弟结点;易于实现找结点孩子等的操作;转化后的二叉树的右子树必为空
结构特点:firstchild+data+nextsibling
typedef struct CSNode{
Elem data;
struct CSNode
*firstchild, *nextsibling;
} CSNode, *CSTree;
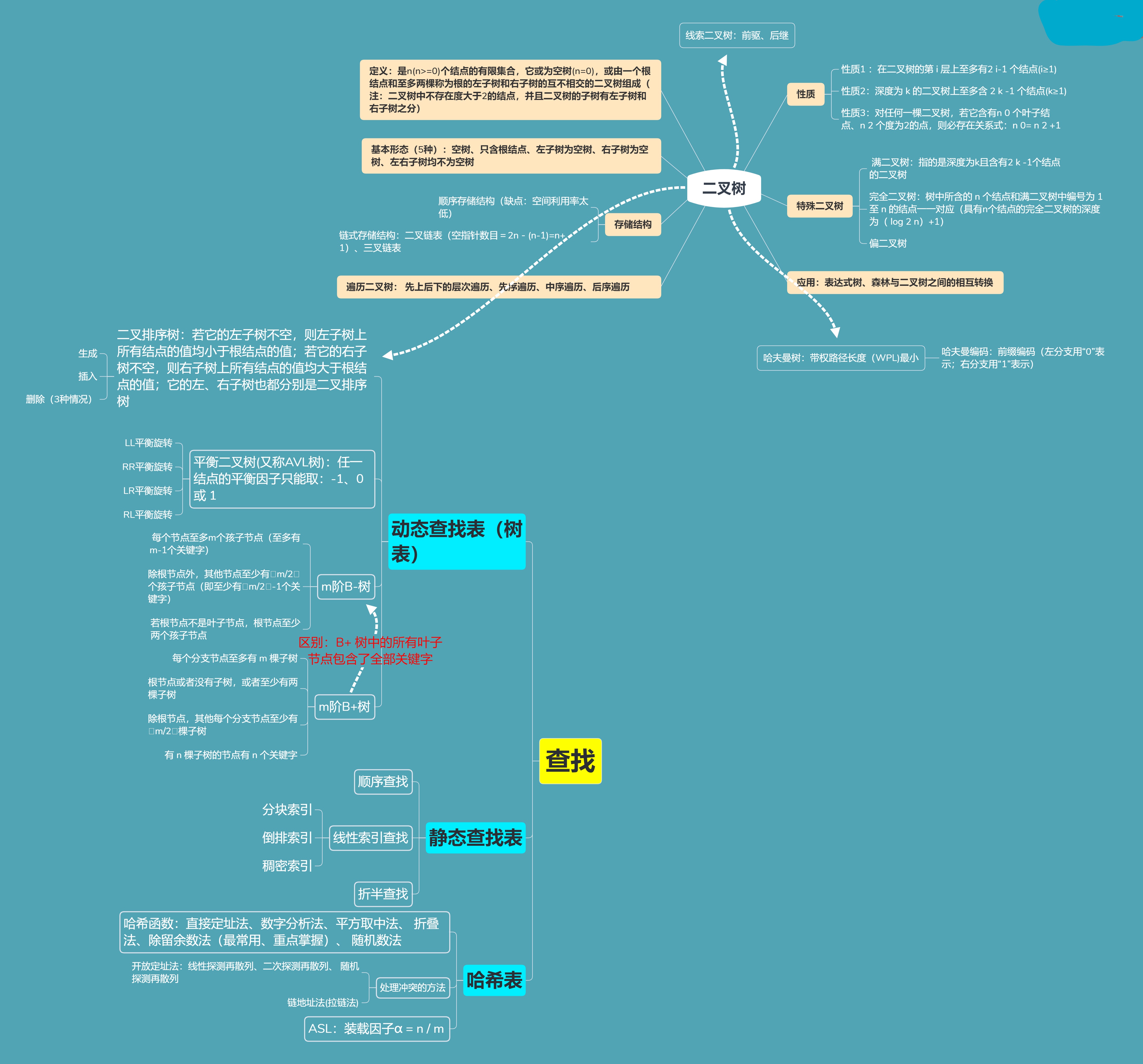
2、二叉树
(1)二叉树的储存结构
a、顺序存储结构
特点:一组地址连续的存储单元存储各结点(如一维数组); 自根而下、自左而右存储结点;按完全二叉树上的结点位置进行编号和存储
typedef struct PTNode {
Elem data;
int parent; // 双亲位置域
} PTNode;
#define MAX_TREE_SIZE 100 // 二叉树的最大结点数
typedef TElemType
SqBiTree[MAX_TREE_SIZE];
// 0号单元存储根结点
SqBiTree bt;
b、链式存储结构
二叉链表:
typedef struct BiTNode {
TElemType data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
三叉链表:
typedef struct TriTNode {
TElemType data;
struct TriTNode *lchild, *rchild;
struct TriTNode *parent; //双亲指针
} TriTNode, *TriTree;
(2)二叉树的遍历
a、二叉树的层次遍历
void Order(bintree*bt){
bintree*ans[101];
int head = 0,tail = 0;
ans[tail++] = bt;
while(head!=tail){
bt = ans[head++];
if(bt){
cout<<bt->data<<" ";
ans[tail++] = bt->left;
ans[tail++] = bt->right;
}
}
}
b、二叉树中序遍历的非递归算法(使用栈):
void InOrderTraverse(BiTree T) {
InitStack(S); p = T;
声明q;//存放栈顶弹出元素
while (p || !StackEmpty(S)) {
if (p) {
Push(S, p);
p = p->lchild;
}
else {
Pop(S, q);
cout << q->data;
p = q->rchild;
}
}
}
(3)线索二叉树:可加快查找节点的前驱或后继的速度
遍历二叉树的结果是:求得结点的一个线性序列;指向该线性序列中的“前驱”和 “后继” 的指针,称作“线索”, 包含“线索”的存储结构,称作“线索链表”,与其相应的二叉树,称作“线索二叉树”
线索链表:
LTag, RTag = 0 代表左右孩子
LTag, RTag = 1 代表线索(L前驱,R后继)
typedef struct BiThrNod {
TElemType data;
struct BiThrNode *lchild, *rchild;// 左右指针
int LTag, RTag; // 左右标志
} BiThrNode, *BiThrTree;
(4)哈夫曼树:带权路径长度取最小值的树
结点的路径长度:从根结点到该结点的路径上分支的数目。
树的路径长度:树中每个结点的路径长度之和。
树的带权路径长度:树中所有叶子结点的带权路径长度之和
3、查找
(1)二叉排序树(中序遍历二叉排序树得到一个关键字的递增有序序列)
a、二叉排序树的查找:
若二叉排序树为空,则查找不成功;否则,若给定值等于根结点的关键字,则查找成功; 若给定值小于根结点的关键字,则继续在左子树上进行查找;若给定值大于根结点的关键字,则继续在右子树上进行查找
查找路径:从根结点出发,沿着左分支或右分支逐层向下直至关键字等于给定值的结点(成功)、从根结点出发,沿着左分支或右分支逐层向下直至指针指向空树为止(不成功)
代码:
BSTree SearchBST(BSTree T, KeyType key) {
if ((!T) || key == T->data.key) return T;
else if (key < T->data.key) //在左子树中继续查找
return SearchBST(T->lchild, key);
else //在右子树中继续查找
return SearchBST(T->rchild, key);
} // SearchBST
查找性能:平均查找长度
最好:log 2 n(形态匀称,与二分查找的判定树相似)
最坏: (n+1)/2(单支树)
b、二叉排序树的插入(插入的元素一定在叶结点上)
若二叉排序树为空,则插入结点应为根结点否则,继续在其左、右子树上查找,树中已有,则不再插入,树中没有,则查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应该为叶子结点的左孩子或右孩子
c、二叉排序树的删除:删除在查找成功之后进行
1)若要删除的结点是叶子节点,则直接删除该节点就可以
2)若要删除的结点是只有左子树或右子树的节点,则令该节点的双亲节点的左孩子或右孩子指向该节点的左孩子或右孩子
3)若要删除的结点是左子树右子树都有的节点,方法一:以其前驱替代T结点,然后再删除该前驱结点,前驱是左子树中最大的结点。方法二:用其后继结点替代T结点,然后删除该后继结点,后继是右子树中最小结点
(2)平衡二叉树(又称AVL树):
二叉排序树的另一种形式,其特点为:树中每个结点左、右子树深度之差(称为平衡因子BF)的绝对值不大于1
(3)B-树(又称多路平衡查找树)
a、插入:插入的位置必定在最下层的非叶结点
插入后,该结点的关键字个数n<m,不修改指针; 插入后,该结点的关键字个数 n=m,则需进行结点分裂”,如果有双亲结点,将k i 插入到双亲结点中;如果没有双亲结点,新建一个双亲结点,树的高度增加一层
b、删除:
首先必须找到待删关键字所在结点,并且要求删除之后,结点中关键字的个数不能小于(m/2 )-1;否则,要从其左(或右)兄弟结点“借调”关键字,若其左和右兄弟结点均无关键字可借(结点中只有最少量的关键字),则必须进行结点的“合并”
(4)B+树(B+树中所有非叶子节点仅起到索引的作用)
a、查找:查找效率高
1)直接从最小关键字开始进行顺序查找所有叶节点链接成的线性链表
2)从B+树的根节点出发一直找到叶节点为止
(5)哈希表
a、构造哈希函数-除留余数法:H(key) = key MOD p
p≤m (表长) 并且p应为不大于 m 的素数或是不含 20 以下的质因子
b、哈希冲突的解决方法:
1)开放地址法:为产生冲突的地址 H(key) 求得一个地址序列
线性探测:d0=h(k);di=(di-1)mod p
二次探测:d0=h(k);di=(d0+-i^2) mod p
2)链地址法(拉链法):将所有哈希地址相同的记录都链接在同一链表中
c、哈希表的查找
决定哈希表查找的ASL的因素:选用的哈希函数;选用的处理冲突的方法;哈希表饱和的程度,装载因子α = n / m
三、.疑难问题及解决方案
1、二叉排序树的删除:删除的结点是左子树右子树都有的结点(未解决)
1、计算成功和不成功时的ASL

我的答案:

查找成功时的ASL=(∑查找次数i×查找次数为i的关键字个数)/关键字总数
不成功ASL:
线性探测:ASL=(∑地址为i到空时的次数)/表长
链地址法:ASL=(0×空的个数+1×第一个结点的个数+2×第二个结点的个数+···)/表长




 浙公网安备 33010602011771号
浙公网安备 33010602011771号