《SCPNet: Unsupervised Cross-modal Homography Estimation via Intra-modal Self-supervised Learning》论文阅读

大家好呀！本文就《SCPNet: Unsupervised Cross-modal Homography Estimation via Intra-modal Self-supervised Learning》这篇论文进行展开来讲解在计算机视觉当中是如何进行图像对齐的。论文的方法主要是通过预测图像相对于目标图像四个角点的偏移量，从而通过单应性变换将原图像投影到目标图像的坐标系下。本文即将从网络模型框架、数据集设置、训练策略、这个三个方面进行讲解。有什么问题的地方，麻烦你提出！我会一直改进，继续加油！
一.网络模型框架

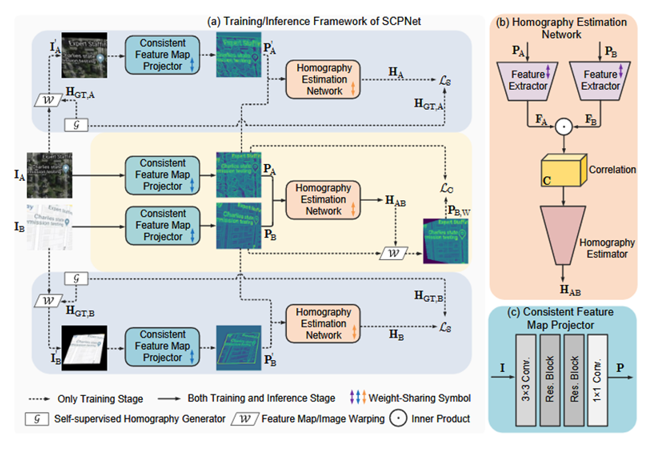
1.1一致性特征图投影
CFMP Projector（Consistency Feature Map，简称 CFMP，CFMP Projector）
主要是将输入的图像转换到与模态无关的特征空间，减少模态间的强度、纹理差异。为什么需要CFMP Projector？因为在不同模态之间的颜色、纹理完全不同，直接对齐像素会失败。在传统方法中仅用像素强度（如亮度）或普通特征匹配无法处理大模态差异。其工作流程具体如下输入图像 → 3×3卷积 → 两个残差块 → 1×1卷积 → 输出1通道的“一致特征图”。在这个投影过程中权重是共享的，不同模态（如卫星图和地图）共用同一个投影器。具体的作用可达到将卫星图和地图的特征映射到同一空间，忽略颜色/纹理差异，只保留几何结构（如道路、建筑的形状）。通过损失函数，强制让投影后的特征图在跨模态图像对齐时尽可能相似。举个例子，你就明白这个投影器了，假设卫星图（A）和地图（B）中都有同一栋楼，但颜色不同。投影器会把A和B中的“楼”都映射成相似的几何轮廓（比如白色线条），这样后续网络更容易计算两者的变换关系。
1.2单应性预测网络
homography estimation network的核心思想是通过特征相关性来匹配两幅图像中的对应点，从而估计变换关系。在图中（b）的流程当中可以看到分别输入Pa与Pb得到两个特征图，F_A和F_B特征图是通过卷积神经网络（CNN）生成的。每个特征图可以看作一个矩阵，矩阵中的每个值表示某个像素区域的特征响应强度。例如：

之后通过通过计算两幅图像的特征图之间的内积，提取模态间的匹配信息，从而为单应性变换的估计提供依据。向量内积是线性代数中的基本运算，用来度量两个向量的相似程度。假设有两个向量 a和 b，它们的内积定义为：

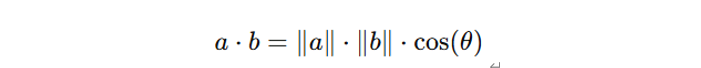
如果两个向量方向一致，内积的值就大；如果方向相反，内积的值为负；如果两个向量垂直，内积的值为 0。在特征空间中，向量的方向和大小反映了图像某处的特征信息。通过计算特征向量的内积，可以衡量模态 A 和模态 B 中对应点的相似性。内积的结果存储在六维相关性矩阵中（表示每个位置的全局匹配关系）。在相关性矩阵中提取局部匹配信息，结合坐标位置生成最终的匹配信息。使用Decoder_32 网络从相关性计算结果中预测图像的单应性四角点的偏移量。最终可得到单应性矩阵。

二.数据工程
(a)GoogleMap

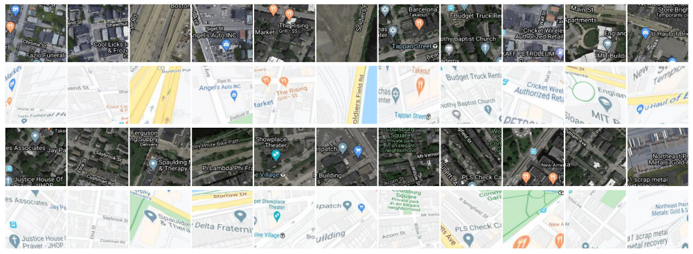
(b)Flash/no-flash

(c)Harvard

(d)RGB/NIR

(e)PDS-COCO

图 (a)(b)(c)(d)(e)：在 [-32，+32] 偏移下，包括 GoogleMap 和 Flash/no-flash在内的跨模态数据集，包括 Harvard 和 RGB/NIR，以及手动制作的不一致数据集 PDS-COCO 的示例图像。
如上述图中显示了跨模态数据集的示例图像，包括 GoogleMap 和 Flash/no-flash ，跨 spetral 数据集包括 Harvard 和 RGB/NIR ，以及手动制作的不一致数据集 PDS-COCO ，偏移量为 [-32，+32]。为了公平比较，所有比较的方法都在每个数据集的相同训练和测试拆分上进行训练和测试。GoogleMap 是一个跨模态数据集，包括相应的卫星和地图图像。我们选择地图图像作为源图像，选择卫星图像作为目标图像。然后，我们使用 中共享的训练和测试数据，大小为 192 × 192。具有同×变形的 128 128 个图像对是通过中心裁剪生成的。单向性的模拟是通过随机扰动 128 × 128 张图像的四个角点来实现的。Flash/no-flash 包含 120 个室内和室外图像对。我们首先将图像大小调整为 320 × 213，然后以与 GoogleMap 相同的方式使用模拟单×生成 128 128 图像对。Harvard 包含 77 个真实世界场景的多光谱图像，每个场景都有 31 个光谱波段，光谱范围为 420nm∼720nm。我们先将图像大小调整为 348 × 260，然后使用每个场景的第 16 波段（即 570nm）图像作为源图像，并通过对其他波段应用模拟单向性来生成目标图像。RGB/NIR 数据集包含 RGB 和 NIR 光谱波段的图像。我们将图像大小调整为 256 × 256，选择 RGB 作为目标图像，选择 NIR 作为源图像以生成单向形变形。从图 3 （d） 中可以看出，RGB/NIR 数据集中有一些低纹理图像，这使得单应性估计任务变得困难。PDS-COCO 人工模拟了 MS-COCO 数据集的亮度、对比度、饱和度和色相噪声的随机组合变化 [10]。与之前类似。
2.2数据处理
2.2.1从数据列表中获取数据

img1 = cv2.imread(self.image_list_img1[index])

img2 = cv2.imread(self.image_list_img2[index])

2.2.2调整图片大小

if self.dataset=='rgbnir':
    img1 = cv2.resize(img1, (256, 256))#调整图像大小
    img2 = cv2.resize(img2, (256, 256))

处理结果如图所示原图为320X224大小经过处理后得到256X256，可以看出图像并未经过剪裁而是经过了一些比例变化

2.2.3转换颜色空间和扩展维度

img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)#转换图像的颜色空间
img1 = np.expand_dims(img1, 2)
img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
img2 = np.expand_dims(img2, 2)

1. cv2.cvtColor()：这个函数用于转换图像的颜色空间。
2. img1：原始图像（通常是一个 3 通道的 BGR 图像）。
3. cv2.COLOR_BGR2GRAY：这个参数告诉 OpenCV 将图像从 BGR 颜色空间转换为灰度（GRAYSCALE）图像。BGR 是 OpenCV 默认的颜色通道顺序。
   如果原始的 img1 是一张彩色图像（例如，大小为 (256, 256, 3)），那么在执行这行代码后，img1 就变成了一张灰度图像，大小变为 (256, 256)，其中每个像素的值是灰度值。
4. np.expand_dims()：这是 NumPy 函数，用于在指定的轴上为数组增加一个新的维度。
   5.img1：已经转换为灰度图像的图像。
   6.• 2：这是新增维度的位置。我们在最后一维（即通道维度）增加一个维度，使得图像由 (256, 256) 变为 (256, 256, 1)
   这行代码将灰度图像的维度从 (256, 256) 扩展为 (256, 256, 1)，这使得 img1 成为一个具有单通道（灰度）图像的三维数组。图像的每个像素现在会被存储为一个单一的数值（而不是三个颜色通道的数值）

如你所看处理后的结果图像

2.2.4.将图像的像素值从 [0, 255] 转换为 [-1, 1] 范围。

img1, img2 = 2*(img1/255.0)-1, 2*(img2/255.0)-1

img1, img2：这是输入的两张图像，它们像素值在 [0, 255] 之间。我们通过 img1/255.0 将其缩放到 [0, 1] 之间，再通过 2*(...) - 1 将其转换到 [-1, 1] 范围内。这个步骤是为了将图像标准化，以便在深度学习中进行处理。

处理后的结果图

2.2.5获取图像尺寸

(height, width, _) = img1.shape

获取 img1 图像的高度（height）、宽度（width）以及通道数（_）。
结果如下：Height: 224, Width: 320, Channels: 1

2.2.6随机裁剪设置

x = random.randint(marginal, width - marginal - patch_size)
y = random.randint(marginal, height - marginal - patch_size)
top_left = (x, y)
bottom_left = (x, patch_size + y - 1)
bottom_right = (patch_size + x - 1, patch_size + y - 1)
top_right = (patch_size + x - 1, y)
four_pts = np.array([top_left, top_right, bottom_left, bottom_right])

1. 随机选择一个 patch_size x patch_size 的裁剪区域，这个区域的左上角坐标是 (x, y)，裁剪区域的四个角是 top_left, top_right, bottom_left, 和 bottom_right，这四个角点被存储在 four_pts 数组中。
2. marginal 代表裁剪区域的边缘留白，避免裁剪出图像边缘。
   结果x: 144
   y: 39
   Top-left: (144, 39)
   Bottom-left: (144, 166)
   Bottom-right: (271, 166)
   Top-right: (271, 39)

3.图像剪裁

img1 = img1[top_left[1]-marginal:bottom_right[1]+marginal+1, top_left[0]-marginal:bottom_right[0]+marginal+1, :]
img2 = img2[top_left[1]-marginal:bottom_right[1]+marginal+1, top_left[0]-marginal:bottom_right[0]+marginal+1, :]
four_pts = four_pts - four_pts[np.newaxis, 0] + marginal # top_left -> (marginal, marginal)
(top_left, top_right, bottom_left, bottom_right) = four_pts

对图像 进行切片操作，提取图像的一个子区域。图像是一个多维数组（通常是三维数组：高 × 宽 × 通道数），切片语法按照三个维度进行：

1. top_left[1]-marginal:bottom_right[1]+marginal+1 ：
   o 这个部分是 y 轴（行） 的切片，用来选择图像的垂直区域（从上到下）。
   o top_left[1] 是裁剪区域的 左上角的 y 坐标，bottom_right[1] 是裁剪区域的 右下角的 y 坐标。
   o 通过调整 top_left[1]-marginal 和 bottom_right[1]+marginal+1，我们可以对裁剪区域的上下边缘进行偏移（增加或减少边缘部分），marginal 可能是一个用于调整边距的参数。
2. top_left[0]-marginal:bottom_right[0]+marginal+1 ：
   o 这个部分是 ****x 轴（列） 的切片，用来选择图像的水平区域（从左到右）。
   o top_left[0] 是裁剪区域的 左上角的 x 坐标，bottom_right[0] 是裁剪区域的 右下角的 x 坐标。
   o 同样，通过调整 top_left[0]-marginal 和 bottom_right[0]+marginal+1，我们可以对裁剪区域的左右边缘进行偏移。
3. : ：
   o 最后一个 : 表示选择 所有通道。如果是灰度图像，最后的 : 选择的是图像的 单通道（没有额外的颜色通道）如果是彩色图像，最后的 : 选择的是所有的颜色通道（如 BGR）
   这段代码使用 NumPy 的切片功能对图像进行裁剪，并加上了额外的边距（marginal）。这种写法是完全正确的，并且是图像处理中常用的技巧。通过这种方式，我们可以从图像中提取出一个特定的区域（包括边缘的留白区域）。

2.2.7.处理四个角点的位置

图像的角点是通过坐标系统来表示的。在计算机中，图像通常是一个二维矩阵，其中每个像素的坐标由 (x, y) 来表示，x 是水平方向的坐标，y 是垂直方向的坐标。图像的四个角点通常指的是图像的四个边界：
• 左上角 (top_left): (0, 0)，即图像的最左上角。
• 右上角 (top_right): (width-1, 0)，即图像的最右上角。
• 左下角 (bottom_left): (0, height-1)，即图像的最左下角。
• 右下角 (bottom_right): (width-1, height-1)，即图像的最右下角。

four_pts - four_pts[np.newaxis, 0] + marginal

这一行代码在做以下操作：
• four_pts[np.newaxis, 0] 是取 four_pts 数组中的第一个点 top_left，并且用 np.newaxis 使得它的形状变为 (1, 2)，变成一个 2D 数组，形如 [[x1, y1]]。np.newaxis 使得我们可以对第一个点进行广播操作。
• 然后，four_pts - four_pts[np.newaxis, 0] 就是将 four_pts 中的所有点的坐标与 top_left 的坐标相减，得到一个新的偏移量数组，这样所有的点都会相对于 top_left 进行平移。
最后，加上 marginal，就是将这个偏移量向所有点添加一个额外的偏移量，通常用于控制裁剪框的偏移。例如，marginal 可能是用来调整图像区域的大小，增加一个边界。
(top_left, top_right, bottom_left, bottom_right) = four_pts
最后，这一行代码将处理过的 four_pts 数组重新赋值给四个变量，表示四个裁剪区域的顶点。将四个角点的坐标偏移，使得裁剪区域的左上角对齐到 (marginal, marginal)，避免裁剪出图像边缘。结果如下：
Updated Four points: [[ 32 32]
[159 32]
[ 32 159]
[159 159]]
2.2.8.随机扰动
好把这个随机扰动就是将图像坐标发生变化

try:
    four_pts_perturb = []
    for i in range(4):
        t1 = random.randint(-perturb, perturb)
        t2 = random.randint(-perturb, perturb)
        four_pts_perturb.append([four_pts[i][0] + t1, four_pts[i][1] + t2])
    org_pts = np.array(four_pts, dtype=np.float32)
    dst_pts = np.array(four_pts_perturb, dtype=np.float32)
    ground_truth = dst_pts - org_pts
    H = cv2.ge****tPerspectiveTransform(org_pts, dst_pts)
    H_inverse = np.linalg.inv(H)

对四个角点施加随机的扰动，生成新的 four_pts_perturb。这个扰动的范围由 perturb 控制。
• org_pts 是原始的四个角点坐标，dst_pts 是经过扰动后的四个角点。
• 计算原始四个角点和变换后四个角点之间的地面真实值（ground_truth），即两个坐标之间的差值。
• 计算透视变换矩阵 H，并获取其逆矩阵 H_inverse，用来将 img2 变换到与 img1 对齐。
当经过扰动后的角点坐标超出了原始图像的边界时，图像的某些部分会超出图像的原始尺寸，而这些超出范围的区域在变换后通常会被填充为灰色或其他默认的值（例如，0，即黑色）。

2.2.10.透视变换

org_pts = np.array(four_pts, dtype=np.float32)
dst_pts = np.array(four_pts_perturb, dtype=np.float32)
ground_truth = dst_pts - org_pts
H = cv2.getPerspectiveTransform(org_pts, dst_pts)
H_inverse = np.linalg.inv(H)

org_pts 和 dst_pts 分别是原始的四个点和扰动后的四个点，它们是用来计算透视变换的。
• org_pts 是原始点集，表示图像中选择的四个角点。
• dst_pts 是扰动后的点集，表示通过随机扰动后的四个角点。
• ground_truth = dst_pts - org_pts 计算了原始点与扰动后点的差值。这个差值就是“地面真相”（ground truth），即真实的位移或偏差。
• cv2.getPerspectiveTransform(org_pts, dst_pts) 使用 OpenCV 提供的 cv2.getPerspectiveTransform 函数，基于 org_pts 和 dst_pts 计算出透视变换矩阵 HHH。透视变换矩阵将原始图像中的四个点变换到扰动后的四个点。
• H_inverse = np.linalg.inv(H) 计算透视变换矩阵 HHH 的逆矩阵 H−1H^{-1}H−1，这是因为在实际应用中，有时需要反向变换，即从扰动后的图像恢复到原始图像的坐标系。

warped_img = cv2.warpPerspective(img2, H_inverse, (img1.shape[1], img1.shape[0]))
warped_img = np.expand_dims(warped_img, 2)

使用 cv2.warpPerspective() 函数将 img2 进行透视变换，得到变换后的图像 warped_img。
• 为了保持一致性，使用 np.expand_dims() 在 warped_img 上增加一个维度，转换为 3D 数组。结果如下：
Original Points (org_pts):
[[ 32. 32.]
[159. 32.]
[ 32. 159.]
[159. 159.]]
Perturbed Points (dst_pts):
[[ 0. 11.]
[131. 10.]
[ 12. 172.]
[157. 129.]]

2.2.11.裁剪图像块

warped_patch = warped_img[top_left[1]:bottom_right[1]+1, top_left[0]:bottom_right[0]+1, :]
non_warped_img = img1
non_warped_patch = non_warped_img[top_left[1]:bottom_right[1]+1, top_left[0]:bottom_right[0]+1, :]

从变换后的图像 warped_img 和未变换的图像 img1 中分别裁剪出一个 patch_size x patch_size 的图像块 warped_patch 和 non_warped_patch。

2.2.12.转换为torch张量

warped_patch = torch.from_numpy(warped_patch).float().permute(2, 0, 1)
non_warped_patch = torch.from_numpy(non_warped_patch).float().permute(2, 0, 1)
warped_img = torch.from_numpy(warped_img).float().permute(2, 0, 1)
non_warped_img**** = torch.from_numpy(non_warped_img).float().permute(2, 0, 1)

将 warped_patch 和 non_warped_patch 转换为 PyTorch 张量，并改变其维度顺序（从 [H, W, C] 转换为 [C, H, W]），以便后续的深度学习处理。
返回多个结果：
• warped_patch: 变换后的图像块。
• non_warped_patch: 未变换的图像块。
• warped_img: 变换后的完整图像。
• non_warped_img: 未变换的完整图像。
• ground_truth: 变换后的四个角点和原始四个角点之间的差值（地面真实值）。
• org_pts: 原始四个角点坐标。
• dst_pts: 变换后四个角点坐标。

三．训练策略
SCPNet 的训练框架包括 两种自监督学习分支 和 一个跨模态学习分支内容如图1（a）。这三种分支同时作用于共享权重的可学习模块，并在训练过程中进行监督。它们的主要目的是通过不同的方式来优化网络，使得网络能够更好地进行图像配准（homography estimation）任务。两个自监督分支分别处理模态A和模态B的内部对齐任务，目的是为了让网络在同一模态内学会基本的单应性估计能力。一个跨模态分支处理模态A和模态B之间的对齐任务，目的是为了让网络学会跨模态对齐。接下来将详细说明每个分支的学习策略

3.1自监督分支
两个自监督分支分别处理模态A和模态B的内部对齐任务，具体以模态A进行详细展开。如图中(a)的训练流程。对一张卫星图I_A施加随机扰动生成I_A’并记录真实的扰动参数H_GT_A。网络最开始输入的是I_A(原始卫星图)和I_A’（扰动后的卫星图）经过网络预测得到扰动参数H_pred_A（即透视变化矩阵），计算H_pred_A和H_GT_A的误差（如MAVCE，即计算损失），反向传播更新网络权重w。对于模态B的图像也同理

3.2跨模态分支
跨模态分支处理模态A和模态B之间的对齐任务，目的是为了让网络学会跨模态对齐。我们使用IA作为目标图像，使用经过随机扰动后的IB’模拟不同视角下的跨模态图像。网络开始输入IA（原始卫星图像）和IB‘(扰动后的地图)经过网络预测得到单应性矩阵H_pred_AB。通过如下进行损失计算反向传播更新网络权重。在跨模态分支中我们并不使用经过随机扰动后得到的真实对齐标签进行损失的计算，具体我们是这样计算的：
论文中跨模态分支的损失函数定义为：

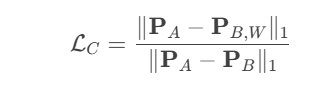
其中：
• PAPA：卫星图（I_A）投影后的一致特征图。
• PBPB：原始地图（I_B）投影后的一致特征图。
• PB,WPB,W：对地图施加预测的单应性变换 HABHAB 后，再投影的特征图。
• ∥⋅∥1∥⋅∥1 表示L1范数（绝对误差和）。
分步解释损失计算
3.2.1 分子部分：||PA−PB,W||1
• 含义：
最小化卫星图的特征图 PAPA 和变换后的地图特征图 PB,WPB,W 之间的差异。
• 作用：
强制网络预测的单应性矩阵 HAB 能够将地图的特征图对齐到卫星图的特征图。
3.2.2 分母部分：||PA−PB||1
• 含义：
最大化卫星图特征图 PA 和原始地图特征图 PB 之间的差异。
• 作用：
防止投影器将所有特征图映射为相同值（即避免退化解）。
3.2.3 整体损失：LC=分子/分母
• 效果：
网络被鼓励同时完成两个目标：

1. 对齐：让变换后的地图特征 PB,W 接近卫星图特征 PA。
2. 区分：保持原始卫星图和地图特征 PA 和 PB 之间的差异。

损失值：
分子越小且分母越大，损失值越小，网络预测的 HAB 越准确

为什么不需要真实标签（H_GT）？
自监督机制：
损失函数通过特征图的对齐程度间接监督网络，而不是直接比较预测的HAB和真实 HGT

核心假设：
如果投影后的特征图能够对齐，则说明预测的单应性矩阵 HAB 是正确的。
无需真实标签的原因：
投影后的特征图已经过滤了颜色/纹理差异，只保留几何结构，对齐特征图即对齐几何结构。
3.3三个分支如何协同工作
• 特征提取器 和 一致特征投影器 在所有分支中共享权重。
• 这意味着：
o 网络在处理卫星图和地图时，使用的是同一套特征提取规则。
o 自监督任务学到的特征表达能力，可以直接迁移到跨模态任务中。
损失函数结合
总损失 = 自监督损失（卫星图） + 自监督损失（地图） + 跨模态损失

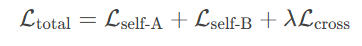
• λ 是跨模态损失的权重（论文中设为0.1）。
• 自监督损失：强制网络学会同一模态内的对齐能力（基础技能）。
• 跨模态损失：强制网络学会跨模态对齐（高阶技能）。

所有分支共享同一网络参数，通过总损失联合优化！

3.4为什么需要三个分支

1. 自监督分支的作用：
   o 相当于“基础训练”，让网络先在简单的任务（同一模态对齐）中掌握单应性估计的基本能力。
   o 如果没有自监督分支，网络可能无法直接处理复杂的跨模态差异。
2. 跨模态分支的作用：
   o 相当于“实战训练”，让网络在基础能力上，进一步适应跨模态的挑战（颜色、纹理差异）。
3. 协同效应：
   o 自监督任务提供“几何变换的先验知识”，跨模态任务利用这些知识解决更复杂的问题。