迎龙年浅谈 Binary Indexed Trees

什么是 Binary Indexed Trees？

就是树状数组啦。树状数组，是一种高级数据结构，用于高效地解决某一类问题。

那么这一类问题是什么呢？那么让我们一起来看一下：

问题引入

给定一个序列 \(a\)，给定 \(Q\) 个 \(l,r\)，求 \(\sum_{i=l}^r a_i\)。

这一类问题，我们明显可以暴力枚举，时间复杂度为 \(\Theta(\sum_{i=1}^Q r-l+1)\)。

明显，若 \(l,r\) 过于大，这样也解决不了，因此有了前缀和。

前缀和，是用来统计前 \(\sum_{i=1}^j a_i\)，也就是说，回答每一次查询只需要 \(\Theta(1)\) 即可，即为 \(a_r-a_{l-1}\)。

这种算法在此问题已经算很高级了，但是如果我们改一下：

---

给定一个序列 \(a\)，给定 \(Q\) 个 操作，每次给定 \(opt,l,r\)，分如下 \(2\) 种操作：

• \(opt=1\)，将 \(a_l\) 增加为 \(r\)。

• \(opt=2\)，求 \(\sum_{i=l}^r a_i\)。

这时，暴力枚举最坏的时间复杂度变为了 \(\Theta(\sum_{i=1}^Q r_i-l_i+1)\)，前缀和的最坏时间复杂度则变成了 \(\Theta(Qn)\)。

因此，我们有了树状数组或者线段树，虽然它们对于每次操作都是 \(\mathcal O(log n)\)，但是线段树应用范围更广，但是这里采用树状数组解决，因为它实现更简单。但是等你都熟练了之后，你会发现，只不过是多了几行代码而已。。。

树状数组的引用

首先我们需要了解一下二进制。

我们知道，任意一个整数 \(x\) 都可以分为 \(2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_m}\)。

设 \(a_1>a_2>a_3>\ldots>a_m\)，则最多可以分解为 \(\log n\) 的区间。

• 区间 \(1\) 长度为 \(2^{a_1}\)，表示范围为 \([1,2^{a_1}]\)。

• 区间 \(2\) 长度为 \(2^{a_2}\)，表示范围为 \([2^{a_1}+1,2^{a_1}+2^{a_2}]\)。

\(\ldots\ldots\ldots\ldots\)

• 区间 \(m\) 长度为 \(2_{a_m}\)，表示范围为 \([2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_{m-1}}+1,2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_m}]\)。

因此，区间 \([l,r]\) 的长度为 \(2^{\texttt{r 的二进制末尾 0 个数}}\)，也就是 \(r\) 最右边的 \(1\) 所代表的数。

我们编程通常用 lowbit(x) 表示，计算方法为 \(x\operatorname{and}(x\operatorname{xor}(x-1))=x\operatorname{and}(-x)\)。

这其实涉及到计算机补码的知识，可以自己百度一下。

inline int lowbit(int x){
	return x&-x;//有无括号无所谓啦。
}

---

树状数组是一种基于二进制思想的数据结构，用来维护序列的前缀和。
—— 网上的一句话。

也就是说，我们可以用 \(tree_i\) 表示 \(\sum_{i=x-\operatorname{lowbit(x)}+1}^x a_i\)。

那么我们不难得到如下图（非原创）：

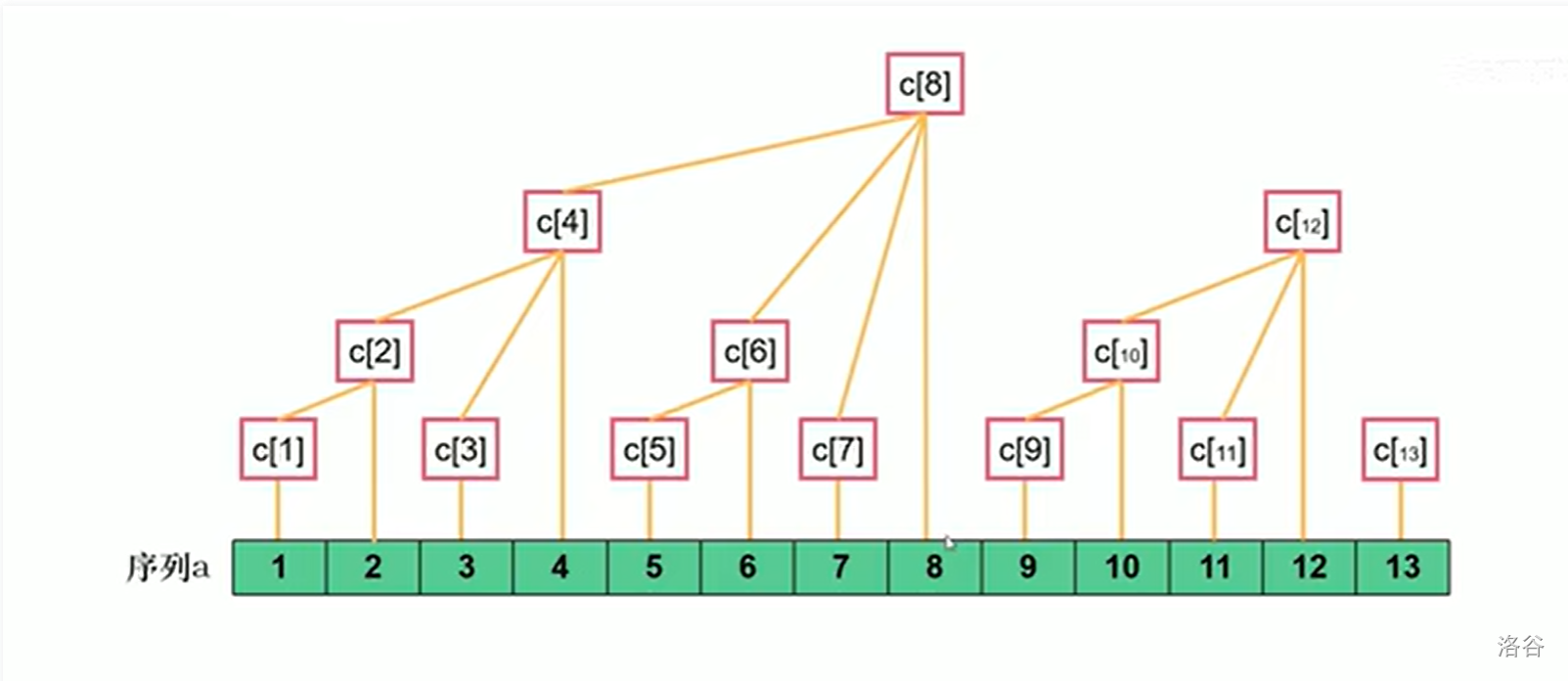
把 \(c\) 当成 \(tree\) 吧。。。

为什么 \(tree_8\) 连接了 \(tree_7,tree_6,tree_4\) 以及 \(a_8\) 呢？首先 \(a_8\) 不用解释了，然后 \(7+lowbit(7)=8\)，\(6+lowbit(6)=8\)，\(4+lowbit(4)=8\)。

单点修改

如果对于 \(a_x\) 进行修改，那么 \(tree_x\sim tree_n\) 的值都会进行变化，因此可以用一个循环将满足条件的 \(tree_y\gets tree_y+a_i\)：

inline void updata(int k,int x){
	for(;k<=n;k+=lowbit(k))//每次增加 lowbit(k)。
    	tree[k]+=x;
}

区间查询

很明显，最好理解，每次减少 \(lowbit(i)\)，并且累加 \(tree_i\) 即可。

inline int query(int k){
	int sum=0;
	for(;k>0;k-=lowbit(k))
    	sum+=tree[k];//累加，不理解建议看看前面的 tree[i] 的表示。
	return sum;

求区间和就 \(query(r)-query(l-1)\) 就行啦（就是前缀和思想）。

初始化

很简单，每次 \(updata(i,a_i)\) 即可，时间复杂度为 \(\Theta(n\log n)\)。

但是还有一种 \(\Theta(n)\) 的方法，考虑每个节点对父亲节点的贡献为 \(tree_i\)，因此代码如下：

for(int i=1;i<=n;i++){
	tree[i]+=a[i];
	if(i+lowbit(i)<=n) //不要越界。
    tree[i+lowbit(i)]+=tree[i];

例题

以下代码都是本蒟蒻早期时打的代码，没有优化，纯 cin,cout。

• 【模板】树状数组 \(1\)。（单点修改 \(+\) 区间查询）

就是上面说的两种操作，直接背模板即可。

#include <bits/stdc++.h>
using namespace std;
#define int long long

const int N=5e5+10;
int n,q,x,y,a,opt,tree[N];

inline int lowbit(int x){//lowbit 函数求解。
    return x&-x;
}
inline int query(int k){//模板。
	int sum=0;
    for(;k>0;k-=lowbit(k)) sum+=tree[k];
	return sum;
}
inline void update(int k,int x){//模板。
    for(;k<=n;k+=lowbit(k)) tree[k]+=x;
}
signed main() {
	cin>>n>>q;
	for(int i=1;i<=n;++i){
        cin>>a;
        update(i,a);//建立树状数组。
    }
    while(q--){
        cin>>opt>>x>>y;
        if(opt==1) update(x,y);//单点修改。
        else cout<<query(y)-query(x-1)<<endl;//区间查询。
    }
	return 0;
}

---

• 【模板】树状数组 \(2\)。（区间修改 \(+\) 单点查询）

这其实涉及到两种操作，即为区间修改以及单点查询。

如果还是用上面的方法去做，时间复杂度可能会达到 \(\Theta(Qn)\)。

所以这种方法是不可行的。

考虑差分，没学过建议学一学。

比如：\(a=[1,2,6,11,12,16,15]\)，那么差分数组 \(b=[1,1,4,5,1,4,-1]\)。（逃

也就是说，\(b_i = a_i - a_{i-1}\)。

很好证明，\(a_i = \sum_{j=1}^i b_j\)，因为 \(a_i - a_{i-1} + (a_{i-1} - a_{i-1}) + \ldots + (a_2 - a_1) + (a_1-[a_0\to 0]) = a_i\)。

所以说，我们可以用树状数组维护差分数组，并不用维护原数组。

但是将 \([l,r]\) 都加上 \(x\) 怎么操作呢？我们可以举了栗子：

比如：\(a=[1,4,9,16,25,36,49]\)，\(b=[1,3,5,7,9,11,13]\)，将 \([2,5]\) 都加上 \(5\)，那么原数组为 \([1,9,14,21,30,36,49]\)，差分数组就为变为 \([1,8,5,7,9,6,13]\)。

仔细观察，我们发现：\([l,r]\) 区间内差分数组 \((l,r]\) 内的没有变，然而 \(b_l\gets b_l+x\)，\(b_r\gets b_r-x\)。

设 \(i\) 在 \((l,r]\) 之间，则更改后 \(b_i = (a_i+x) -(a_{i-1}+x)=a_i-a_{i-1}\)，不会发生变化。

但是 \(i=l\)，\(b_i = (a_i + x) - (a_{i-1}) = a_i - a_{i-1}+x=b_i+x\);\(i=r+1\)，\(b_i = a_i - (a_{i-1}+x)=a_i-a_{i-1}-x=b_i-x\)。

因此，我们只需要对两个端点进行单点修改即可。

update(l,x);//增加。
update(r+1,-x);//减少。

那么怎么输出呢？

因为 \(a_i = \sum_{j=1}^i b_j\)，上面有证明，所以直接查询就行了（反正维护的是差分数组）。

\(\boxed{Code}\)

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,q,x,y,s,a[N],opt,tree[N];
inline int lowbit(int x){
    return x&-x;
}
inline int query(int k){
	int sum=0;
    for(;k>0;k-=lowbit(k)) sum+=tree[k];
	return sum;
}
inline void update(int k,int x){
    for(;k<=n;k+=lowbit(k)) tree[k]+=x;
}
signed main() {
	cin>>n>>q;
	for(int i=1;i<=n;++i){
        cin>>a[i];
        update(i,a[i]-a[i-1]);//维护差分数组，O(n) 也可以，只不过 O(n log n) 更容易实现。
    }
    while(q--){
        cin>>opt;
        if(opt==1){
            cin>>x>>y>>s;
            update(x,s);
            update(y+1,-s);//做两次正确的单点修改即为区间修改。
        }
        else{
            cin>>x;
            cout<<query(x)<<endl;//输出。
        }
    }
	return 0;
}

---

• AcWing. 一个简单的整数问题 \(2\)（区间修改 \(+\) 区间查询）

发一个图：

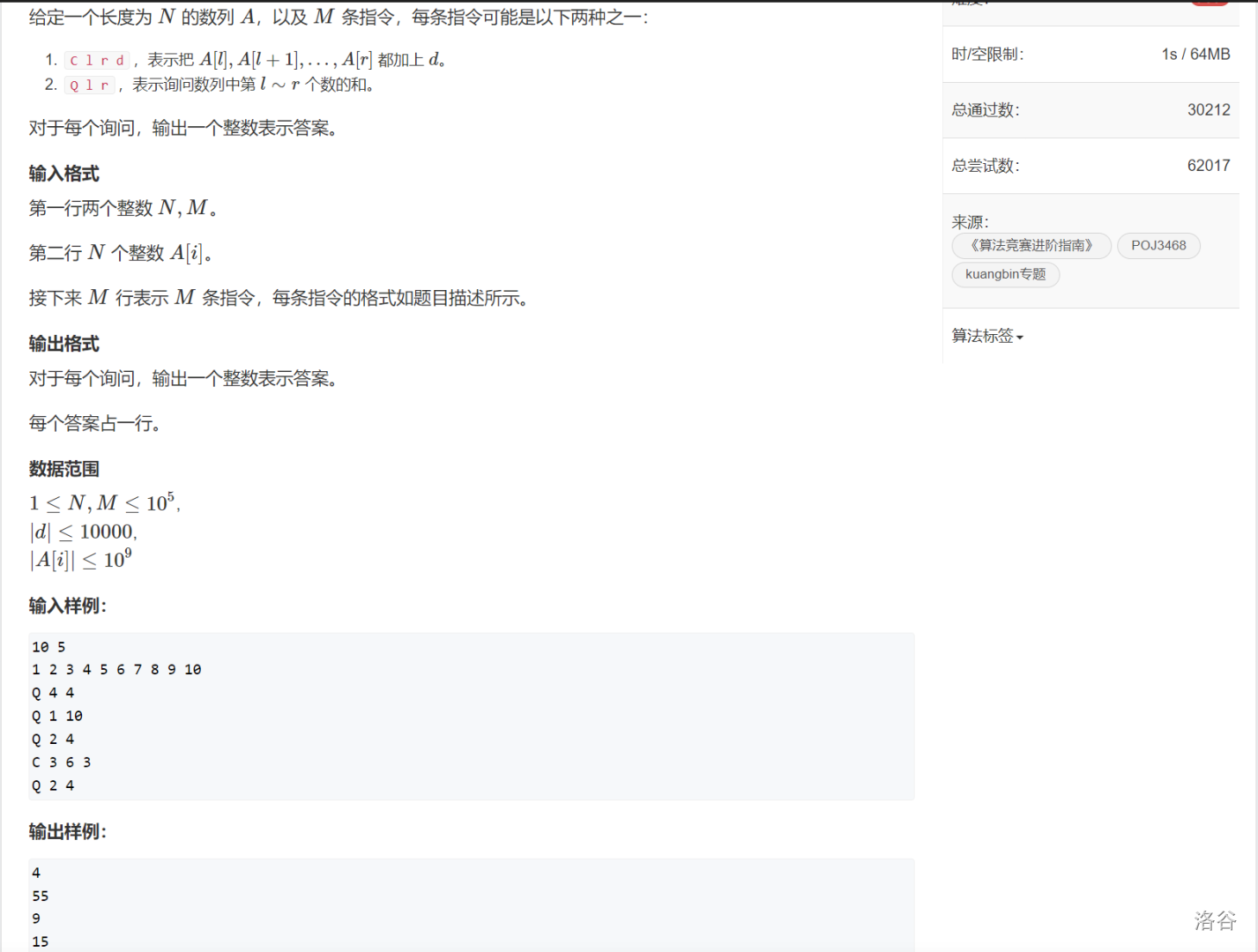
看到区间修改，我们还是要用树状数组维护差分数组。

但是看到区间查询，如果单是只用差分数组，用到我们上面证明的 \(a_i = \sum_{j=1}^i b_j\)，一次查询的时间复杂度为 \(\mathcal O((r-l+1)\log n)\)，这不妥妥的 T 呀。

还是根据证明的 \(a_i = \sum_{j=1}^i b_i\)，则求原数组的前缀和为：

\[s_1 = b_1 \]

\[s_2 = a_1 + a_2=b_1+b_1+b_2 \]

\[s_3=a_1+a_2+a_3=b_1+b_1+b_2+b_1+b_2+b_3 \]

\[\cdots\cdots \]

\[s_n = \sum_{i=1}^n a_i = \sum_{i=1}^n b_i\times (n-i+1) \]

手工绘画一下（不是矩阵快速幂的矩阵）：

\[\begin{bmatrix}\color{red}{b_1}&\color{red}{b_2}&\color{red}{b_3}&\color{red}{\cdots}&\color{red}{b_n}\\b_1 &\color{red}b_2 & \color{red}{b_3} & \color{red}\cdots & \color{red}{b_n}\\b_1&b_2&\color{red}{b_3}&\color{red}\cdots&\color{red}{b_n}\\b_1&b_2&b_3&\color{red}{\cdots}&\color{red}{b_n}\\\cdots&\cdots&\cdots\cdots&\color{red}{\cdots}&\color{red}{\cdots}\\b_1&b_2&b_3&\cdots&b_n\end{bmatrix} \]

上面矩阵的源码：$$\begin{bmatrix}\color{red}{b_1}&\color{red}{b_2}&\color{red}{b_3}&\color{red}{\cdots}&\color{red}{b_n}\\b_1 &\color{red}b_2 & \color{red}{b_3} & \color{red}\cdots & \color{red}{b_n}\\b_1&b_2&\color{red}{b_3}&\color{red}\cdots&\color{red}{b_n}\\b_1&b_2&b_3&\color{red}{\cdots}&\color{red}{b_n}\\\cdots&\cdots&\cdots\cdots&\color{red}{\cdots}&\color{red}{\cdots}\\b_1&b_2&b_3&\cdots&b_n\end{bmatrix}$$

那么：

\[\begin{aligned}s_n &= (b_1+b_2+\cdots+b_n)\times (n+1)-(b_1\times 1+b_2\times 2+\cdots+n\times b_n)\\ &=\sum_{i=1}^n b_i \ \times (n+1) - \sum_{i=1}^n i\times b_i\end{aligned} \]

所以，额外用一个树状数组维护一个 \(i\cdot d_i\) 的差分数组即可。

\(\boxed{Code}\)

注：代码是别人的，我这道题用线段树 A 了，树状数组就不用了。我在代码上多加几条注释。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;
int n, m;
int a[N];
LL tr[N], tri[N];
//tr[]数组是对原数组的差分数组 d[] 进行维护，而 tri[] 数组是对原书的的差分数组 d[] * i 进行维护。

int lowbit(int x)
{
    return x & -x;
}
void add(LL c[], int x, int v)
{
    for (int i = x; i <= n; i += lowbit(i))
        c[i] += v;
}
LL query(LL c[], int x)
{
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += c[i];
    return res;
}

LL get_sum(int x)
{
    return query(tr, x) * (x + 1) - query(tri, x);//公式。
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i])
    for (int i = 1; i <= n; ++i) 
        tr[i] = a[i] - a[i - 1], tri[i] = tr[i] * i;//构造数组。
    /*建树。*/
    for (int x = 1; x <= n; ++x)
        for (int i = x - 1; i >= x - lowbit(x) + 1; i -= lowbit(i))
            tr[x] += tr[i], tri[x] += tri[i];
//-----------------------------------------------------------------
    while (m--){
        char op[2];
        int l, r, c;
        scanf("%s", op);
        if (op[0] == 'Q')
        {
            scanf("%d%d", &l, &r);
            printf("%lld\n", get_sum(r) - get_sum(l - 1));//类似于前缀和思想。
        }
        else
        {
            scanf("%d%d%d", &l, &r, &c);
            add(tr, l, c), add(tr, r + 1, -c);
            add(tri, l, l * c), add(tri, r + 1, (r + 1) * -c);//单点修改，很好理解的，就是多了一个数组。
        }
    }
    return 0;
}

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/44886/
来源：AcWing

---

• 最接近神的人。（树状数组求逆序对个数）

一眼望去，就是求序列里逆序对的个数，于是乎我们 \(\mathcal O(n^2)\) T 了。

仔细看看数据，\(1\le n\le 5\times 10^5\)。

那么这类问题涉及到了树状数组的另一个作用：求逆序对！

由于原本的数组 \(a\) 过于庞大，我们考虑离散化。

将序列 \(a\) 从大到小排序，如果值相同则按照位置从大到小排序。

这样，相同的值就不会被统计逆序对了。

随后，我们考虑用树状数组维护：

• 已知，一开始，\(\forall tree_i= 0\)。

• 然后开始遍历，设当前值为 \(x\)，位置为 \(v\)。

• 首先查询树状数组 \(v-1\) 的位置，查找大于 \(x\) 的数的个数（这样才能形成逆序对，即 \(a_i > a_j\)）。

• 然后对 \(v\) 位置以及其后的 \(tree_y\) 做 \(+1\) 操作，因为已经排序，所以该点对后面的贡献为 \(1\)。

时间复杂度为 \(\mathcal O(n\log n)\)。

\(\boxed{Code}\)

//笔者：可以复制哦。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,ans,tree[N]；
struct node{
    int num,pos;
};
node a[N];
inline bool cmp(node s1,node s2){
    if(s1.num==s2.num) return s1.pos>s2.pos;
    return s1.num>s2.num;
}
inline int lowbit(int x){
    return x&-x;
}
inline int query(int k){
	int sum=0;
    for(;k>0;k-=lowbit(k)) ans+=tree[k];
	return sum;
}
inline void update(int k){
    for(;k<=n;k+=lowbit(k)) tree[k]++;//直接 ++。
}
signed main() {
	cin>>n;
	for(int i=1;i<=n;++i){
        cin>>a[i].num;
        a[i].pos=i;//记录位置。
       //这种情况下可以不用建树，一开始没有遍历过答案就是 0，并没有初始数组。
    }
	sort(a+1,a+1+n,cmp);
	for(int i=1;i<=n;i++) {
		ans+=query(a[i].pos-1);//查询。
		update(a[i].pos);//修改，做贡献。
	}
	cout<<ans<<endl;
	return 0;
}

• 异或橙子。（操作 \(+\rightarrow \oplus\) 以及 \(\oplus\) 的一些性质）

挺不错的，只不过是有一些性质。

我们都知道，异或的运算法则：相同则 \(0\)，不同则 \(1\)。

因此如下性质：

• \(a \oplus a=0\)

（自己异或自己，二进制一模一样，每一位都相同，肯定是 \(0\)）。

• \(a\oplus 0 = a\)

（相当于每一位都异或 \(0\)，分情况讨论。设 \(a_i\) 表示 \(a\) 的二进制第 \(i\) 位，如果 \(a_i = 1\)，则 \(1\oplus 0=1\)，一样；若 \(a_i = 0\)，则 \(0\oplus 0=0\)，一样。所以 \(a\oplus 0 = a\)）。

通过计算，设序列长度为 \(len\)，则第 \(i\) 个数会出现 \(\sum_{j=1}^i (n-j+1) - (i-j)= \sum_{j=1}^i n-i+1 = i\times (n-i+1)\)。

分情况讨论：

• 如果 \(2\mid n\)。

  • 如果 \(2\mid i\)，则任何 \(2\mid i\) 的数出现的次数都是偶数次。

  • 如果 \(2\mid (i+1)\)，则 \(n-i+1\) 为偶数，则任何 \(2\mid (i+1)\) 的数都会出现偶数次。

• 如果 \(2\mid (n+1)\)。

  • 如果 \(2\mid i\)，则 \((n-i+1)\) 为偶数，则任何 \(2\mid i\) 的数都会出现偶数次。

  • 若 \(2\mid (i+1)\)，则两端都是奇数，奇数 \(\times\) 奇数 \(=\) 奇数，所以任何 \(2\mid (i+1)\) 的数都会出现奇数次。

因为偶数次为根据性质 \(1\) 抵消变为 \(0\)，而 \(0\) 又会根据性质 \(2\) 完全没有作用，因此：

• 若 \(2\mid (r-l+1)\)，则答案为 \(0\)。

• 若 \(2\mid (r-l)\)，则答案为 \(a_l \oplus a_{l+2} \oplus a_{l+4}\oplus\ldots \oplus a_r\)。

这样该怎么求呢？我们可以开两个树状数组维护右端点分别为奇偶数的情况呀！

那么原本的加法运算怎么办呢？那都改为异或运算不就好了嘛！

\(\boxed{Code}\)

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,q,x,y,opt,ans,a[N];
inline int lowbit(int x){
    return x&-x;
}
struct node{//定义在结构体更方便。
    int xx[N];
    inline int query(int k){//区间查询。
	    int sum=0;
        for(;k>0;k-=lowbit(k)) sum^=xx[k];
	    return sum;
    }
    inline void update(int k,int x){//单点修改。
        for(;k<=n;k+=lowbit(k)) xx[k]^=x;
    }
};
node tree[3];
signed main() {
	cin>>n>>q;
	for(int i=1;i<=n;++i){
        cin>>a[i];
        tree[i&1].update(i,a[i]);//建树。
    }
	while(q--){
        cin>>opt>>x>>y;
        if(opt==1){
            tree[x&1].update(x,a[x]^y);//别忘了修改哈，把 a[x] 修改为 y 就是异或 a[x]^y。
            a[x]=y;
        }
        else
            if(!((y-x+1)&1)) cout<<"0\n";//区间个数为偶数，答案为 0.
            else cout<<((tree[x&1].query(x-1))^(tree[x&1].query(y)))<<endl;//否则维护即可。
        
    }
	return 0;
}

• 数星星 Stars。（\(2\) 个参数的树状数组）

选择暴力，时间复杂度为 \(\mathcal O(n^2)\)，可能勉强能卡过。但是如果改成 \(1\le n\le 10^5\)，那不就妥妥的 T 了吗？

所以暴力是不可行的。

题目要求 \(x_j \le x_i \ \Lambda\ y_j<y_i\)，有两个参数 \(x\) 和 \(y\)，那么我们可以先将 \(n\) 个星星的 \(x\)，\(y\) 坐标进行从小到大的排序，来让树状数组更简单地实现。

以 \(x\) 为第一关键字，\(y\) 为第二关键字，每次遍历 \(n\) 颗星星。

既然此时 \(x\) 已经排好序，那么对于 \(y_i\) 的等级，就是 \(\sum_{k=1}^{i-1} [y_k\le y_i]\)。

这时发现，这不就是树状数组吗？用一个 \(\texttt{query}(y_i)\) 就解决了。

然后考虑第 \(i\) 颗星星对于以后的星星的贡献都为 \(1\)，因此 \(\texttt{update}(y_i,1)\) 就解决了。

那么怎么统计等级为 \(x\) 的星星个数呢？我们可以开一个桶呀！

\(\boxed{Code}\)

//笔者的话：可以复制哦。
#include <bits/stdc++.h>
using namespace std;

#define lowbit(x) x&(-x)
#define int long long
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define rrep(i,x,y) for(int i=x;i>=y;i--)
#define sc scanf
#define pr printf
inline int read(){int s=0,w=1;char c=getchar();while(!isdigit(c)){if(c=='-') w=-1;c=getchar();}while(isdigit(c)){s=(s<<1)+(s<<3)+(c^48);c=getchar();}return s*w;}

const int N=1e6+10;
int n,maxny,ans[N],tree[N];

struct stars{
    int x,y;
    bool operator <(const stars &t)const{//重载运算符。
        if(x==t.x) return y<t.y;
        return x<t.x;
    }
}a[N];

//以下都是树状数组模板。
inline void update(int k,int t){
    for(k;k<=maxny;k+=lowbit(k))//注意不是 <=n，是 <=maxny（最大的 y 坐标）。
        tree[k]+=t;
}

inline int query(int k){
    int sum=0;
    for(k;k>0;k-=lowbit(k))
        sum+=tree[k];
    return sum;
}

signed main(){
    n=read();
    rep(i,1,n){
        a[i].x=read();
        a[i].y=read();
        ++a[i].x;
        ++a[i].y;
        maxny=max(maxny,a[i].y);//比较最大的 y 坐标。
      //这里也不用建树，理由同上。
    }
	
	sort(a+1,a+1+n);
  
    rep(i,1,n){
        ans[query(a[i].y)]++;//统计答案。
        update(a[i].y,1);//单点修改 ---> 对后面的树状数组做贡献。
    }
    rep(i,1,n)
        pr("%lld\n",ans[i-1]);
    return 0;
}

未完待续。。。