2025 贵阳 代码源 Day 7 模拟赛

Day 7 模拟赛

A

发现 \(\lceil \frac{X+Y}{X|Y} \rceil=1+[X \& Y>0]\)，又有题目给定的 \(m\le4\) 可以想到暴力容斥做，分别求出包含 \(1\to4\) 个相同位置的数量然后容斥原理就好了。

B

分讨，发现有同一种字符出现了两个长度大于 \(k\) 的连续段会炸，两种字符都只有一个长度大于 \(k\) 的连续段就一定可以，判完这两种情况剩下的只剩下只有一种字符出现了一个这样的连续段，如果这个连续段长度 \(\ge 2k-1\) 就炸了，否则找有没有一个不同种的字符，使它后面的字符也是不同种的，或者使得这个字符后面的与连续段相同种类的字符的连续段长度 \(+\) 这个连续段长度 \(-k+1<k\)。用图表示就是存在 \(\begin{matrix} \underbrace{AAA\dots AAA} \\ x>k \end{matrix}\begin{matrix}B \underbrace{AAA\dots AAA} \\ y<k-x+k-1 \end{matrix}\) 或 \(\begin{matrix} \underbrace{AAA\dots AAA} \\x>k \end{matrix}\ \begin{matrix}\underbrace{B\dots B} \\y>1\end{matrix}\) 即为可行，注意这是向后找，向前找也是同理。

C

看到要求最小值最大，考虑二分，发现 \(k\) 很小，想到状压。在二分中 dp，\(f_{i,j}\) 表示完成了字符集合 \(i\)，使用字符串的前缀 \(1\to j\) 是否可行。发现复杂度 \(O(n2^k)\)，考虑优化。发现 \(f_{i,j}\) 可行，则 \(f_{i,j+1}\) 也可行，便考虑优化状态表示。改成 \(f_i\) 表示完成字符集合 \(i\) 所用的最短前缀，再用一个 \(d_{i,j}\) 表示从 \(i\) 出发，字符为 \(j\)，第一个长度能满足我们二分的值的连续段的开始位置，这样转移就成了 \(f_{i|j}\gets d_{f_i,j}+x\)，这里我们每次二分预处理 \(d\) 数组复杂度 \(O(nk)\)，总复杂度 \(O(nk+2^k)\)。

D

这里不使用官解使用我们学长 chi_li 大人的另一种实现方法。

发现单点修改区间查询考虑线段树，维护区间内 4 个信息 \(sum,edt,mnt,fai\)，分别表示：区间内 \(t\) 的总和，也就是 \(l\) 走到 \(r+1\) 位置最短总耗时（注意是 \(r+1\) 方便区间合并）；如果我们在 \(x_l\) 时刻开始走这个区间，最早的结束时间；如果我们要保证整个区间可行（也就是不会让任何人超时），最晚可能的开始时间；这个区间是否不可能被走完。

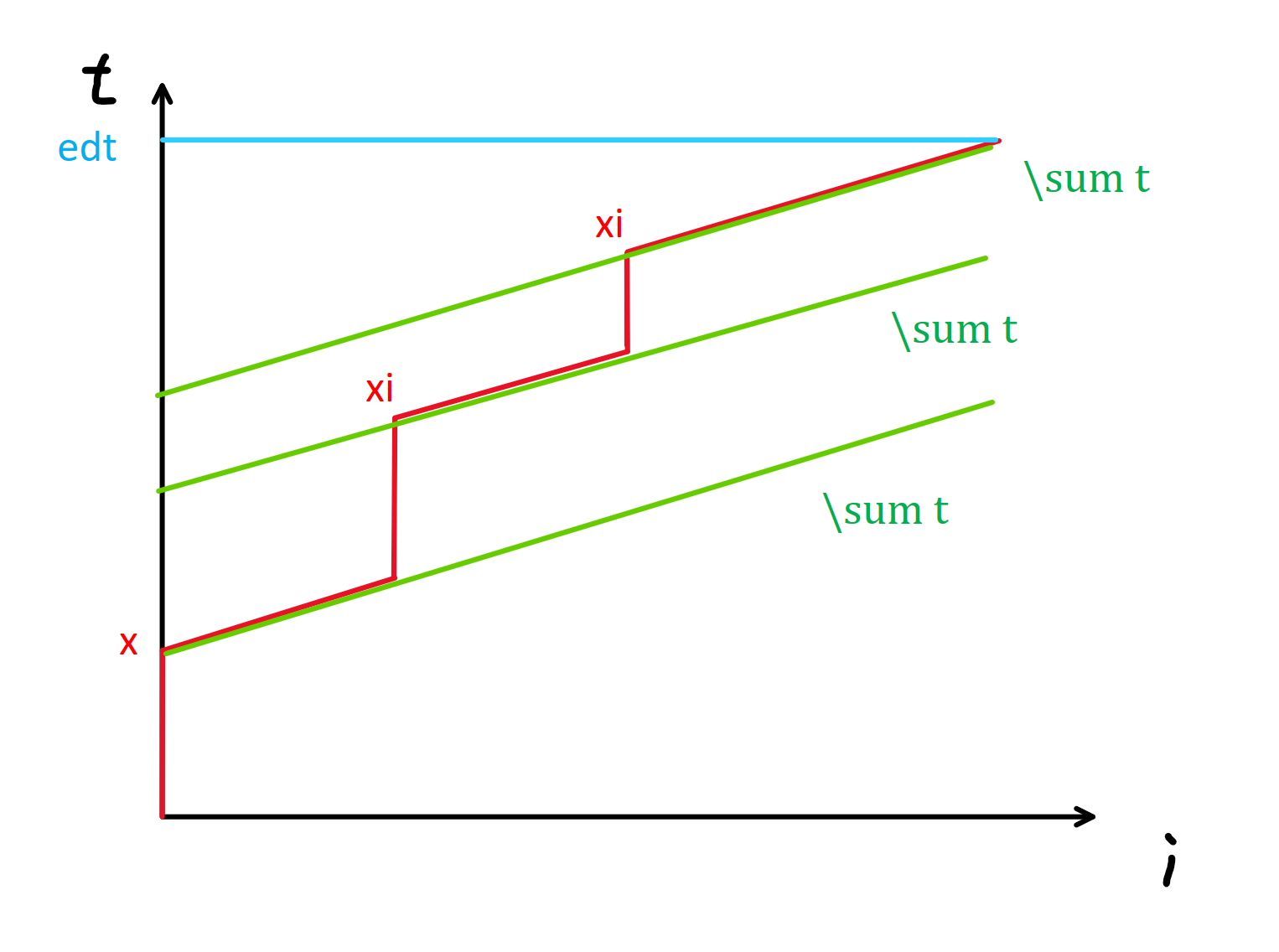
有了定义后我们考虑区间内你到达的位置和时间的关系，两者必然如下图。

这时我们考虑 \(edt\) 是如何计算的，发现我们可以直接枚举 \(i\) 认定为 \(i\) 就是最后一个等待 \(x_i\) 的位置进行计算，最后再取一个 \(\max\)，这样我们就一定能找到真正的最后一个等待的位置并求出它的值。写成公式即为 \(edt=\max\limits_{i=l}^r(x_i+\sum\limits_{j=i}^rt_j)\)，下图中的绿线更好说明了这点。

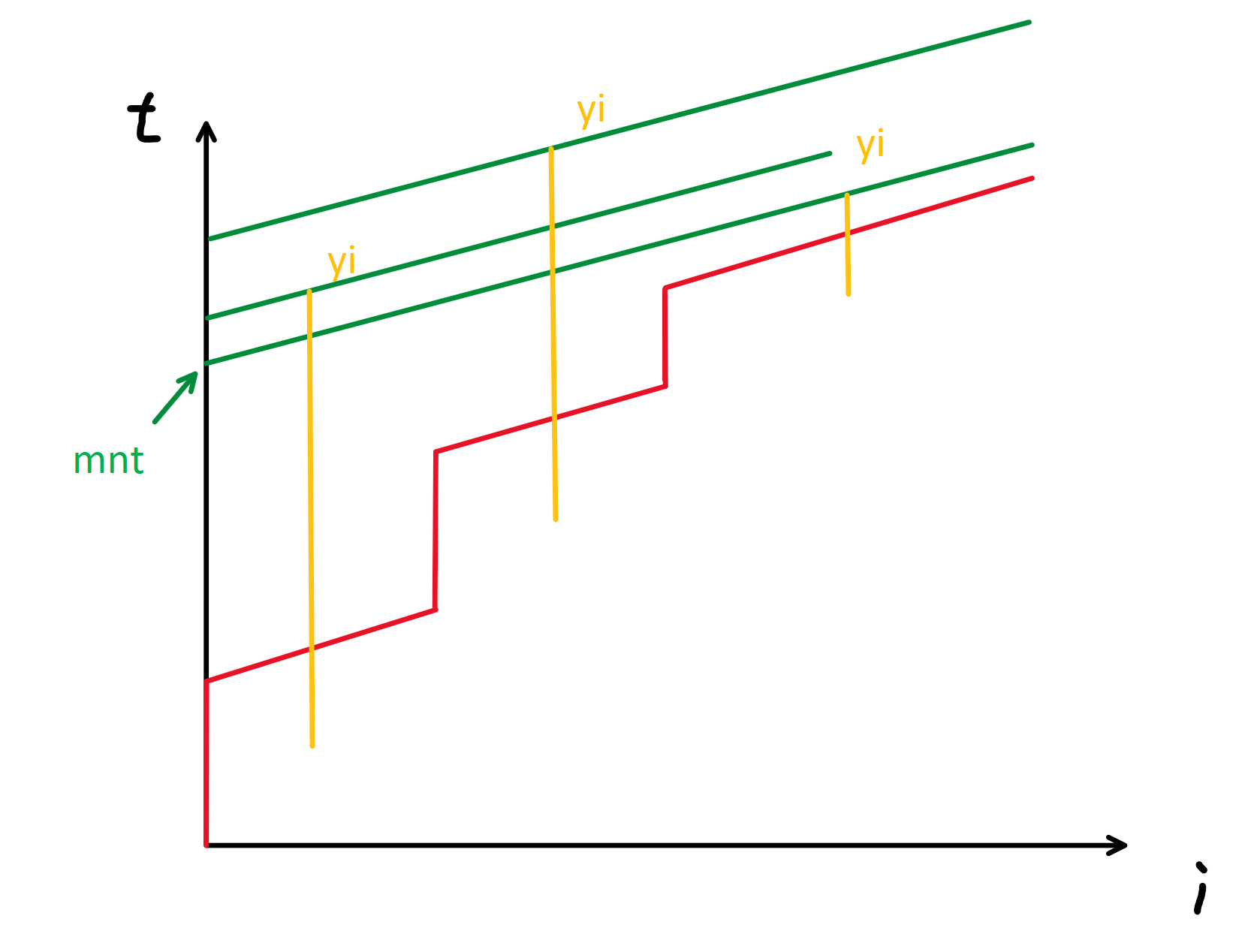
现在我们考虑 \(mnt\)，发现它的计算方式跟 \(edt\) 很相似，但这回我们需要用 \(y_i\) 取 \(\min\) 并计算其与 \(\sum t\) 的差，写成公式即为 \(mnt=\min\limits_{i=l}^r(y_i-\sum\limits_{j=1}^{i-1}t_j)\)。如下图。

接下来我们考虑最关键的，如何在线段树上 push_up，同时也是统计答案时的 merge。先考虑 \(edt\)，发现由于其中加上了一个 \(t\) 的后缀和，便想到可以从 \(edt_{rson}\) 直接转移而不用修改其值，而由于 \(edt_{lson}\) 少统计了一段后缀，便 \(edt_{lson}+sum_{rson}\) 便能正好补上缺失的后缀和，将左右儿子的值取 \(\max\) 即可。发现 \(mnt\) 和 \(edt\) 同理，只是取 \(\min\) 并减去前缀，便为 \(mnt=\min(mnt_{lson},mnt_{rson}-sum_{lson})\)。

剩下的就只有单点修改和区间查询，修改好维护，查询时考虑像最大子段和一样用一个 merge 将左右两个子树的答案合并在一起，merge 的写法和 push_up 一模一样，这样便做完了。

All code