2024/10/2 CSP-S daimayuan模拟赛复盘

2024/10/2 CSP-S daimayuan

contest link (Day 7)

A. 序列

题面描述

给你一个序列 \(r_1,r_2,\dots,r_n\)，问有多少非负整数序列 \(x_1,x_2,\dots,x_n\) 满足：

• 对于所有 \(i\)，\(0 \leq x_i \leq r_i\)。

• 满足 \(x_1|x_2|\dots|x_n=x_1+x_2+\dots+x_n\)，左边为二进制或。

输出答案对 \(998244353\) 取模的结果。

输入 & 输出 & 样例 & 数据范围

输入第一行一个整数 \(n\)。

接下来一行，一共 \(n\) 个整数 \(r_1,r_2,\dots,r_n\)。

输出一个整数，表示答案。

对于所有数据，保证 \(1 \leq n \leq 16,0 \leq r_i < 260\)。

5
1 2 3 4 5

思路解析

首先考虑将那个按位或的条件转换一下，可以得到条件等价于要求对于所有的 \((i,j)\) 都有 \(x_i \& x_j=0\)，相当于我们查看所有 \(x\) 的第 \(k\) 位，只有一个或没有 \(x\) 在当前位上为 \(1\)。有这种想法后我们就可以想数位 dp，但是在二进制数位下。我们在常规的数位 dp 下需要记录是否有顶头，这里同理，但是需要记录 \(n\) 个元素的信息，因为 \(n\) 的范围较小，用状压存储即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 18, M = 64;
const ll P = 998244353;
ll n, r[N], f[2][1 << N];
int g(ll x, int y) {
	return (x >> y) & 1; 
}
int main() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> r[i];
	f[63 & 1][0] = 1;
	for(int i = 62; i >= 0; i--) {
		for(int j = 0; j < (1 << n); j++) f[i & 1][j] = 0;
		for(int j = 0; j < (1 << n); j++) {
			int tmp = 0;
			for(int k = 1; k <= n; k++) {
				if(g(j, k - 1) || g(r[k], i)) tmp += (1 << (k - 1));
			}
			f[i & 1][tmp] += f[(i + 1) & 1][j];
			for(int k = 1; k <= n; k++) {
				int top = ((g(j, k - 1) || g(r[k], i)) ? 1 : 0);
				if(g(j, k - 1) || g(r[k], i)) {
					int now = ((tmp ^ (1 << (k - 1))) | ((g(j, k - 1)) << (k - 1)));
					f[i & 1][now] += f[(i + 1) & 1][j]; f[i & 1][now] %= P;
				}
			}
		}
	}
	ll ans = 0;
	for(int j = 0; j < (1 << n); j++) ans = (ans + f[0][j]) % P;
	cout << ans;
	return 0;
}

B. 合并数字

题面描述

有 \(n\) 个数字，\(a_1,a_2,\dots,a_n\)。每次可以选择两个数字 \(x,y\) 删除，然后加入数字 \(K-x-y\)。\(n-1\) 轮之后只剩下一个数字，问最后剩下的数字最大可能是多少？

你要对 \(q\) 个不同的 \(K\) 进行回答。每组询问独立，都是对于一开始的序列操作。

输入 & 输出 & 样例 & 数据范围

输入第一行两个整数 \(n,q\)。

接下来一行 \(n\) 个整数 \(a_1,a_2,\dots,a_n\)。

接下来一行 \(q\) 个整数 \(K_1,K_2,\dots,K_q\)，表示每次询问的值。

输出一共 \(q\) 行，每行一个整数，表示答案。

对于所有数据，保证 \(1 \leq n,q \leq 3 \times 10^5,0 \leq K_i,a_i \leq 10^9\)。

思路解析

通过找规律或打表可以发现最终的答案的式子肯定是形如 \((K \times x)+(a_1+a_2+ \dots +a_{y})-(a_{y+1}+a_{y+2}+ \dots +a_{n})\)，这里我们先将 \(a\) 从大到小排序。接下来我们考虑 \(x\) 和 \(y\) 的关系，我们将我们进行的操作用树的方式表示出来就如下图，其中 \(\pm\) 号就代表 \(K\) 的贡献，\(\pm a\) 就表示 \(a\) 对应的贡献。

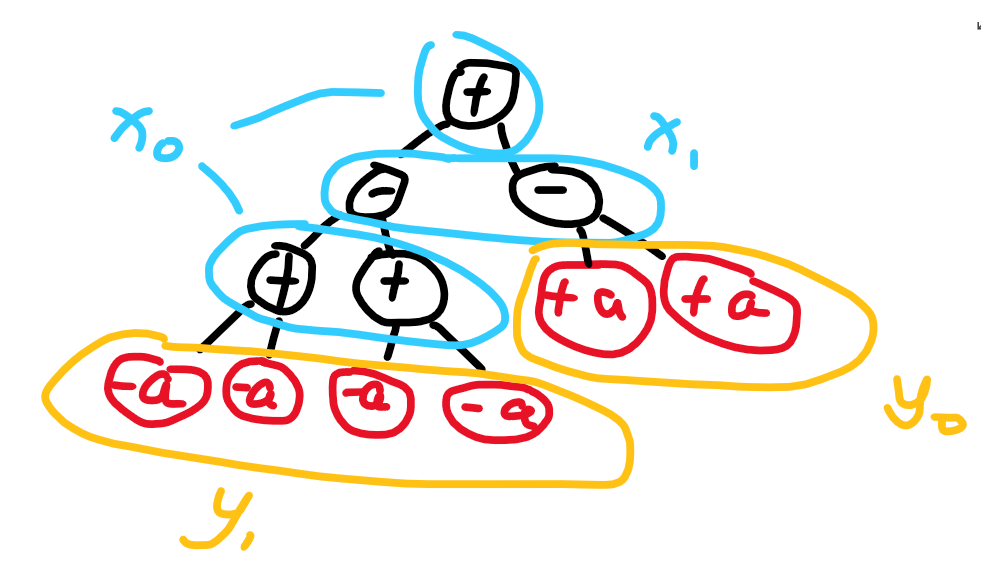
可以发现元素的符号和其深度的奇偶性直接相关，于是我们把 \(+K\) 的个数记为 \(x_0\)，\(-K\) 的个数记为 \(x_1\)，\(\pm a\) 的贡献同理，此时我们和上面的答案式子对应就有 \(x=x_0-x_1,y=y_0-y_1\)。接下来可以通过树的性质发现 \(2 \times x_0 = x_1+y_1, 2 \times x_1=x_0+y_0-1\)，这样我们根据 \(y_0+y_1=n,x_0+x_1=n-1\) 解方程就能得到 \(y=\frac{n+1-x}{3}\)。现在我们已经知道了 \(x,y\) 之间的函数关系式，以及在确定 \(x,y\) 后答案的值，这样我们就可以以 \(y\) 或 \(x\) 和 \((K \times x)+(a_1+a_2+ \dots +a_{y})-(a_{y+1}+a_{y+2}+ \dots +a_{n})\) 建出一个函数，可以发现该函数是单峰的，于是可以使用三分解决。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e5 + 10;
int n, Q, a[N], s[N];
bool cmp(int x, int y) {
	return x > y;
}
int calc(int k, int x, int y) {
	if(x < 0) return -2e9;
	return 2ll * s[x] - s[n] + k * y;
}
signed main() {
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> n >> Q;
	for(int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + n + 1, cmp);
	for(int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
	int x = (2 * n - 1) % 3, y = (n + 1 - x) / 3;
//	cout << "  " << x << ' ' << y << ' ' << calc(3, x + 3 * 0, y - 2 * 0) << '\n';
	while(Q--) {
		int k; cin >> k;
		int l = 0, r = (n - x) / 3;
//		cout << "    " << l << ' ' << r << '\n';
		while(l <= r) {
			int ml = l + (r - l + 1) / 3, mr = ml + (r - l + 1) / 3;
			if(calc(k, x + 3 * ml, y - 2 * ml) > calc(k, x + 3 * mr, y - 2 * mr)) r = mr - 1;
			else l = ml + 1;
//			cout << "    " << l << ' ' << r << '\n';
		}
		int ans = max(max(calc(k, x + 3 * l, y - 2 * l), calc(k, x + 3 * r, y - 2 * r)), max(calc(k, x + 3 * l + 3, y - 2 * l - 2), calc(k, x + 3 * r - 3, y - 2 * r + 2)));
		cout << ans << '\n';
	}
	return 0;
}