ABC211 复盘
ABC211 复盘
[ABC211C] chokudai
思路解析
题目说的很明白,看到匹配子序列可以轻易想到是简单 dp,直接做即可。
时间复杂度:两个字符串两层循环,\(O(8 \times N)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const long long mod = 1e9 + 7;
string t = " chokudai";
string s;
long long f[15];
int main() {
cin >> s;
s = ' ' + s;
f[0] = 1;
for(int i = 1; i < s.size(); i++) {
for(int j = 1; j <= 8; j++) {
if(s[i] == t[j]) {
f[j] = (f[j] + f[j - 1]) % mod;
}
}
}
cout << f[8];
return 0;
}
[ABC211D] Number of Shortest paths
思路解析
题目其实说得很明白了,就是最短路计数。我们可以用一个 \(s_i\) 表示从起点到 \(i\) 的最短路计数,然后进行 bfs,由于边权为 \(1\),所以可以使用 bfs 求最短路。如果 \(u \to v\) 是 \(v\) 的最短路的其中一段,就把 \(s_u \to s_v\) 转移即可。
注意要记得取模。
时间复杂度:bfs,复杂度 \(O(N)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int n, m, d[N], s[N];
vector<int> g[N];
void bfs() {
memset(d, 0x3f, sizeof(d));
d[1] = 0; s[1] = 1;
queue<int> q;
q.push(1);
while(!q.empty()) {
int u = q.front(); q.pop();
for(auto it : g[u]) {
if(d[it] >= d[u] + 1) {
if(d[it] > 1e8) q.push(it);
d[it] = d[u] + 1;
s[it] = (s[it] + s[u]) % mod;
}
}
}
}
int main() {
cin >> n >> m;
for(int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
bfs();
cout << s[n];
return 0;
}
[ABC211E] Red Polyomino
思路解析
可见直接枚举每个格子是否着色会 TLE,于是可以想到 dfs,dfs(x) 表示我们已经用了 \(x\) 个红色方格,然后只找周围又红色格子的白格子转移,然后只要在每一个 dfs 里只进行一次递归后就返回,就可以避免 TLE 和重复方案。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int n, k, ans = 0;
char ch[N][N];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
bool check(int x, int y) {
return (x > 0 && x <= n && y > 0 && y <= n);
}
void dfs(int c) {
if(c == k) return (void)(ans++);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(ch[i][j] == '.') {
bool flag = false;
for(int d = 0; d < 4; d++) {
int nx = i + dx[d], ny = j + dy[d];
flag |= (check(nx, ny) && (ch[nx][ny] == '@'));
}
if(flag || c == 0) {
ch[i][j] = '@'; dfs(c + 1);
ch[i][j] = '#'; dfs(c);
ch[i][j] = '.';
return;
}
}
}
}
}
int main() {
cin >> n >> k;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
cin >> ch[i][j];
}
}
dfs(0);
cout << ans;
return 0;
}
[ABC211F] Rectilinear Polygons
思路解析
先说结论:扫描线。顾名思义,扫描线的本质就是用一条线沿着 \(x\) 或 \(y\) 轴扫过去,每碰到一条边就记录一下加边后是面积是增加还是减少,然后用树状数组或线段树统计。由于我们并不需要知道整张图所有的位置的值,我们就只需要求出来扫描线所在的那一行 or 列每一个点的值即可。
这里就不过多解释,如果没有学过扫描线建议去做一下模板题 ,推荐看第一篇题解。
接下来就是本题的重点,该如何把不规则图形存下来。如下图,我们先把图上的竖边找出来,同时给点的顺序标一个号。
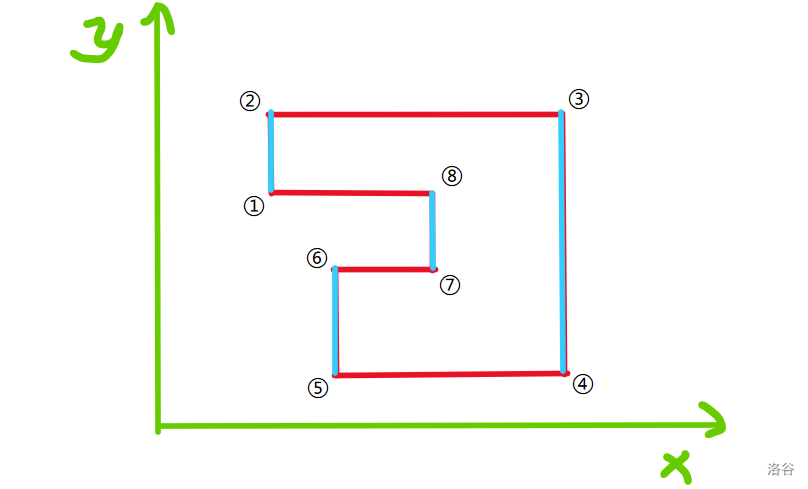
可见四条边中左边三条的权值都是增加的,只有右边一条是减少的。我们寻找边上的两点和权值的关系,可以发现,由于是点顺序输入的,所以每一条正边权的边的两点中编号较小的点 \(y\) 值也是更小的,而每一条边的两点中编号较小的点的编号一定是奇数。因此我们可以给每一条边都判断两点编号的大小来决定是用正边权还是负边权。
实现
我们根据以上所说的方式存好每一条边,然后将边按 \(x\) 的值排序,满足扫描线的性质。对于询问我们将询问离线下来,同样按 \(x\) 排序,这样我们在进行加边之前判断当前扫描线是否已经处理了所有 \(x\) 小于当前询问的 \(x\) 的边,若已经处理完就更新答案。
接下来有几点注意事项。
- 题目中的输入点的顺序不一定满足我们想要的输入顺序,所以我们需要自己找到一个在 \(x\) 最小的情况下 \(y\) 也最小的点做编号为 \(1\) 的点。
- 由于我们只需要知道一个点被覆盖的次数,所以可以将模板中的线段树换成树状数组区修单查。
- 由于我们需要先把当前 \(x\) 轴上的边加完再统计询问,所以我们要在所有边的最后加上一个 \(x=\inf,val=0\) 的边,这样就能防止最后有几个点没有处理到。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 1e5;
int n, m, xx[N], yy[N], tv[N], q, c[N], ans[N];
struct side {
int x, ya, yb, val;
};
struct point {
int x, ya, yb;
};
struct query {
int x, y, p;
};
void add(int x, int y) {
for(; x <= M; x += (x & -x)) {
c[x] += y;
}
}
int ask(int x) {
int sum = 0;
for(; x > 0; x -= (x & -x)) {
sum += c[x];
}
return sum;
}
int main() {
cin >> n;
vector<side> v;
for(int i = 1; i <= n; i++) {
cin >> m;
for(int i = 0; i < m; i++) {
cin >> xx[i] >> yy[i];
xx[i]++; yy[i]++;
}
int p = 0;
for(int i = 0; i < m; i++) {
if(xx[i] == xx[p] && yy[i] < yy[p]) p = i; //找到起始点,注意 y 轴也要判
else if(xx[i] < xx[p]) p = i;
}
int val = 1;
for(int i = 0; i < m; i++) {
int w = (i + p) % m;
tv[w] = val; //给点加权
val = -val;
}
for(int i = 0; i < m; i += 2) { //判断
if(yy[i] < yy[i + 1]) v.push_back({xx[i], yy[i], yy[i + 1], tv[i]});
else v.push_back({xx[i], yy[i + 1], yy[i], tv[i + 1]});
}
}
sort(v.begin(), v.end(), [](side x, side y) { //按 x 排序
if(x.x != y.x) return x.x < y.x;
else return x.ya < y.ya;
});
v.push_back({M + 1, 1, 1, 0}); //避免结尾有点没判
vector<query> que;
cin >> q;
for(int i = 1; i <= q; i++) {
cin >> xx[i] >> yy[i];
xx[i]++; yy[i]++;
que.push_back({xx[i], yy[i], i}); //离线
}
sort(que.begin(), que.end(), [](query x, query y) { //排序
if(x.x != y.x) return x.x < y.x;
else return x.y < y.y;
});
int pos = 0;
for(auto it : v) {
int x = it.x, ya = it.ya, yb = it.yb, val = it.val;
for(; que[pos].x < x && pos < (int)que.size(); pos++) {
ans[que[pos].p] = ask(que[pos].y); //若已经操作完则更新
}
add(ya, val); add(yb, -val); //加权
}
for(int i = 1; i <= q; i++) cout << ans[i] << '\n';
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号