ABC219 复盘
ABC219 复盘
[ABC219A] AtCoder Quiz 2
思路解析
直接判断 \(x\) 属于的区间然后输出即可。
时间复杂度:直接判断,\(O(1)\)。
code
#include<bits/stdc++.h>
using namespace std;
int x;
int main() {
cin >> x;
if(x < 40) cout << 40 - x; //直接判断即可
else if(x >= 40 && x < 70) cout << 70 - x;
else if(x >= 70 && x < 90) cout << 90 - x;
else if(x >= 90) cout << "expert";
return 0;
}
[ABC219B] Maritozzo
思路解析
将输入的三个字符串用数组存下来,这样拼接时就直接调用下标即可。
时间复杂度:需要遍历 \(T\) 中的每个字符,\(O(\left\vert T \right\vert)\)。
code
#include<bits/stdc++.h>
using namespace std;
string s[10], t;
int main() {
cin >> s[1] >> s[2] >> s[3];
cin >> t;
for(int i = 0; i < t.size(); i++) {
cout << s[t[i] - '0']; //直接输出对应下标的字符串即可
}
return 0;
}
[ABC219C] Neo-lexicographic Ordering
思路解析
既然要将字母重新排列,那我们就可以直接将字符串中对应字符给替换为给定的字母顺序,然后按照编译器自带的运算符排序即可,记得最后要转换回原来输入的字符。
时间复杂度:首先需要将字符串替换掉,还要进行一次排序,复杂度为 \(O(N\left\vert S \right\vert + N \log N)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
string x, s[N], t[N];
char z[130], c[130];
int main() {
cin >> x;
for(int i = 0; i < 26; i++) {
z[x[i]] = 'a' + i;
c['a' + i] = x[i];
}
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> s[i];
for(int j = 0; j < s[i].size(); j++) {
s[i][j] = z[s[i][j]]; //直接将字符串替换掉
}
}
sort(s + 1, s + n + 1); //排序
for(int i = 1; i <= n; i++) {
for(int j = 0; j < s[i].size(); j++) {
s[i][j] = c[s[i][j]]; //最后替换回来
}
cout << s[i] << '\n';
}
return 0;
}
[ABC219D] Strange Lunchbox
思路解析
可以发现 \(x,y \le 300\) 可用费用背包做,费用就是每道菜有 \(1\) 的费用。注意如果全选价值最大能到 \(300 \times 300\),三维的 dp 内存会炸,于是我们发现答案只需要 \(\sum a_i \ge x,\sum b_i \ge y\),所以我们可以把大于等于 \(x\) 或 \(y\) 的价值全部计算到 \(x,y\) 上,这样值域就只有 \(300\),答案就是 \(f_{n,x,y}\)。
注意如果不存在合法方案要输出 -1。
时间复杂度:三维 dp,每维分别是当前遍历到了第几道菜,价值 1 和价值 2,总复杂度 \(O(nxy)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 310;
int n, x, y, a[N], b[N], f[N][N][N];
int main() {
cin >> n >> x >> y;
for(int i = 1; i <= n; i++) {
cin >> a[i] >> b[i];
}
memset(f, 0x3f, sizeof(f));
f[0][0][0] = 0;
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= x; j++) {
for(int k = 0; k <= y; k++) {
f[i][j][k] = min(f[i][j][k], f[i - 1][j][k]);
int nx = min(j + a[i], x), ny = min(k + b[i], y); //如果大于 x,y 就直接把答案记在 x,y 上
f[i][nx][ny] = min(f[i][nx][ny], f[i - 1][j][k] + 1);
}
}
}
if(f[n][x][y] < 1e8) cout << f[n][x][y];
else cout << -1;
return 0;
}
[ABC219E] Moat
思路解析
一眼看到输入数据只有 \(4\) 行 \(4\) 列,直接想到状压枚举。可以直接枚举所有护城河所包含起来的格子,判断是否连通以及判断是否包含住了所有村庄。判断连通我选择用洪水填充,随便选一个包含着的格子,若可以通过当前格移动到所有被包含格就说明连通。以及还要判断被包围格子是否形成了一个环,例如:
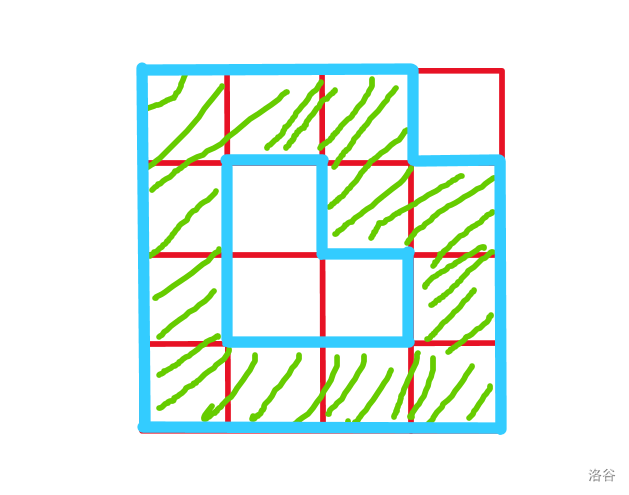
其中蓝线表示护城河,绿色阴影表示护城河包围的格子。可见图中有两条护城河,不符合题意。为排除掉这种情况,我们判断每一个没有被选择的格子,判断它是否被护城河完全包围,也就是判断能否走到地图外即可。
时间复杂度:首先一次暴力枚举,然后对于每种情况需要判断是否为可行方案,洪水填充最多遍历 \(16\) 个格子,复杂度为 \(2^{16} \times 16\)。
code
#include<bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define fir first
#define sec second
int v[8][8], flag[8][8], f[8][8], ans = 0;
bool vis[8][8];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
void flood(int x, int y) {
queue< PII > q;
q.push({x, y});
while(!q.empty()) {
int xx = q.front().fir, yy = q.front().sec;
q.pop();
for(int i = 0; i < 4; i++) {
int nx = xx + dx[i], ny = yy + dy[i];
if(flag[nx][ny] && !f[nx][ny]) {
f[nx][ny] = true;
q.push({nx, ny});
}
}
}
}
bool flood_loop(int x, int y) {
queue< PII > q;
q.push({x, y});
memset(vis, false, sizeof(vis));
vis[x][y] = true;
while(!q.empty()) {
int xx = q.front().fir, yy = q.front().sec;
q.pop();
for(int i = 0; i < 4; i++) {
int nx = xx + dx[i], ny = yy + dy[i];
if(!flag[nx][ny] && !vis[nx][ny]) {
if(nx >= 1 && nx <= 4 && ny >= 1 && ny <= 4) {
vis[nx][ny] = true;
q.push({nx, ny});
}
else return true;
}
}
}
return false;
}
int check() {
int x = 0, y = 0, cnt = 0;
for(int i = 1; i <= 4; i++) {
for(int j = 1; j <= 4; j++) {
if(flag[i][j]) cnt++, x = i, y = j;
}
}
memset(f, 0, sizeof(f));
f[x][y] = 1;
flood(x, y); //洪水填充判断连通
int sum = 0;
for(int i = 1; i <= 4; i++) {
for(int j = 1; j <= 4; j++) {
if(f[i][j]) sum++;
}
}
if(sum != cnt) return 0; //不连通
for(int i = 1; i <= 4; i++) {
for(int j = 1; j <= 4; j++) {
if(v[i][j] && !f[i][j]) return 0; //若有村庄没被包含
}
}
for(int i = 1; i <= 4; i++) {
for(int j = 1; j <= 4; j++) {
if(!flag[i][j] && !flood_loop(i, j)) return 0; //被护城河完全包围
}
}
return 1;
}
void dfs(int x, int y) { //暴力枚举
if(y > 4) y = 1, x++;
if(x > 4) {
ans += check();
return;
}
flag[x][y] = 1;
dfs(x, y + 1);
flag[x][y] = 0;
dfs(x, y + 1);
}
int main() {
for(int i = 1; i <= 4; i++) {
for(int j = 1; j <= 4; j++) {
cin >> v[i][j];
}
}
dfs(1, 1);
cout << ans;
return 0;
}
[ABC219F] Cleaning Robot
思路解析
要点:将整个图拆分成每一轮的每一个点单独考虑贡献。
首先看到 \(k \le 10^{12}\) 发现不能直接枚举 \(k\) 轮,于是开始找每一轮的规律。首先可以知道,如果操作固定,那么起点和路径上每一个点以及终点的相对位置不会改变。也就是说每一轮的起点之间的相对位置,我们记作每一轮的偏移量,其实是不会改变的。若不理解,请看下图。
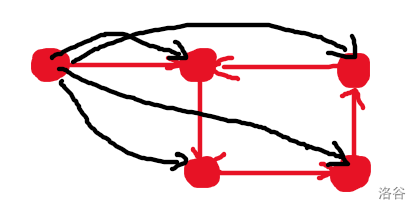
其中红线代表经过的位置和线路,黑线代表起点与各个点之间的偏移量。由此可见不论如何移动起点,它移动所形成的形状是不会改变的。
了解完这个规律之后就很好理解了。我们可以先做出来第一次所经过的所有点的位置,由于起点和终点的偏移量不会改变的特点,我们在以后每一轮的这一个操作完后的位置,和上一轮进行完这一个操作之后的位置,偏移量也是不会改变的。若不理解,请看下图。
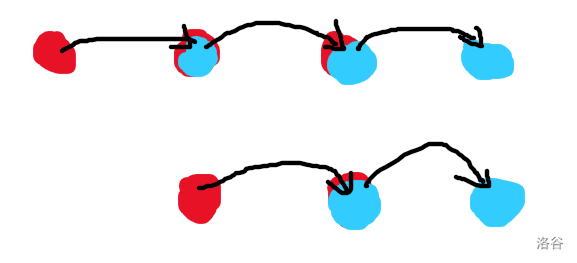
其中红点表示第一次经过的点,蓝点表示第二次经过的点,黑线表示第一轮的当前次序遍历到的点与第二轮的当前次序遍历到的点之间的偏移量。可以发现每一个点的位置与下一轮的位置之间的偏移量也是不会变的,而这个偏移量其实就是每一轮的起点和终点的偏移量,因为每一轮的开始都是上一轮的结束,所以每一轮的起点的偏移量是固定的,那么其他点的偏移量也是固定的。所以这时我们发现,有一些点在下一轮到达了未经过的位置,它对答案造成了贡献(如上图最右边的两个蓝色点),而有一些则又经过了之前已经经过了的其他点,就对答案没有贡献(如上图的其他蓝色点)。
接下来我们则需要思考第一轮中有哪些点对答案有贡献,贡献分别是多少。我们考虑下面这幅图。
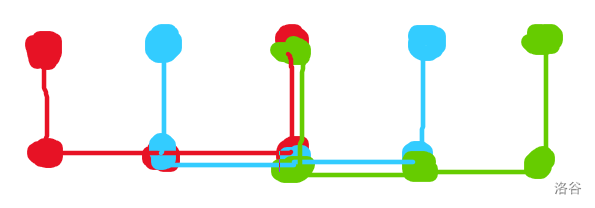
红,蓝,绿点分别表示第一,二,三轮经过的点。我们发现后两轮造成了贡献的点只有三个,分别是 \((0,0),(0,2),(1,2)\) 这三点。而其中 \((0,0)\) 点只造成了 \(1\) 次贡献,并且可以发现该点以后再也不会造成任何贡献。原因是如果我们把一个点增加 \(1 \to k\) 次偏移量的每一种情况都列举出来,如果中途的第 \(i\) 个点在第一轮就被遍历过了,那么第 \(i \to k\) 这些所有的轮数里当前点都不会再有任何贡献。换句话说,当前点对答案的贡献就是 \(i\),因为还有第一轮造成的贡献。
明确了答案统计的方式之后,我们需要计算的值就是对于第一次移动遍历到的每一个点,找到加上 \(i\) 轮偏移量后会与第一轮经过的某一个点重合的最小的 \(i\)。由于每一轮之间的偏移量不变,所以当前点经过 \(k\) 轮移动后所有的点都在同一条斜率为 \(\frac{x}{y}\) 的直线上,其中 \(x,y\) 分别是偏移量的 \(x,y\) 轴。所以问题就变成了对于每一个点,找到经过当前点的斜率为 \(\frac{x}{y}\) 的直线上往后找与当前点最接近的点,计算当前点需要经过多少轮的偏移量才能到达这个点,也就是将距离除以偏移量的值。这里的点指第一轮中经过的所有点。这样我们就可以把每一条直线给找出来,对于每一条直线都用一个 vector 存下这条直线上所有的点与起点之间经过的轮数,设 \(a,b\) 分别为当前点的 \(x,y\) 轴,起点就是 \((a \mod x,b-y\times\lfloor a/x \rfloor)\)。最后的答案就是对于每一条直线,设 \(v_{i}\) 为当前直线上的第 \(i\) 个点,求 \(\sum_{i=1}^{size-1} \min(v_{i+1}-v_{i},k)+k\),因为如果相差轮数大于 \(k\),那么对答案就没有影响,同时最后一个点不会被阻挡,所以要加上 \(k\)。
最后就是几个需要注意的小细节:
- 若 \(x=0,y=0\),就说明之后的每一轮都不会有新的贡献,直接输出第一轮的贡献即可。
- 若 \(x=0,y \ne 0\),为了防止 \(a \mod x\) 没有结果,我们交换 \(x,y\) 和所有的 \(a,b\)。
- 若 \(x<0\),为方便计算,我们取反 \(x\) 和所有的 \(a\)。
code
#include<bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define fir first
#define sec second
string str;
long long k;
vector< PII > v;
int dx[150], dy[150];
void init() {
dx['U'] = -1;
dx['D'] = 1;
dy['L'] = -1;
dy['R'] = 1;
}
signed main() {
init();
cin >> str >> k;
int x = 0, y = 0;
v.push_back({x, y});
for(int i = 0; i < (int)str.size(); i++) {
x += dx[(int)str[i]], y += dy[(int)str[i]];
v.push_back({x, y});
}
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
if(x == 0 && y == 0) {
cout << v.size(); return 0;
}
if(x == 0) {
swap(x, y);
for(auto &it : v) swap(it.fir, it.sec);
}
if(x < 0) {
x = -x;
for(auto &it : v) it.fir = -it.fir;
}
map< PII, vector<int> > mp;
for(auto it : v) {
int nx = it.fir, ny = it.sec;
int mod = (nx % x + x) % x;
mp[{mod, ny - (long long)y * (nx - mod) / x}].push_back((nx - mod) / x);
}
long long ans = 0;
for(auto it : mp) {
sort(it.sec.begin(), it.sec.end());
for(int i = 0; i <= (int)it.sec.size() - 2; i++) {
ans += min(k, (long long)it.sec[i + 1] - it.sec[i]);
}
ans += k;
}
cout << ans;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号