AVL平衡树

AVL平衡树

在百度中，我们可以看到很多篇AVL平衡树的题解

但是——都是封装过的，根本看不懂

于是本蒟蒻决定写一篇蒟蒻能看的懂的AVL题解

正篇开始

首先，我们得先搞懂平衡树是来干啥的，已经会的大牛们可以跳到下一个分割线

其实就是一个平平无奇的二叉排序树，用来查排名之类的

但是，如果你按一定顺序输入的话，它就完美地变成了一个链！

于是我们就得强制他是一个比较满的二叉树（有些不专业

或者说让每个节点的左右子树节点树大概相等，来确保每次查询时间大概是log级别的

于是，阿德尔森-维尔斯与兰迪斯就想到了———可以将树转一转，扭一扭（泡一泡）
就这样，AVL树诞生了

——————————————————————————————————————————

定义

一棵AVL树中所有节点满足以下条件

    1.它的左子树和右子树都是AVL树
    2.|左子树高度-右子树高度|<=1

平衡操作

既然知道了定义，操作就十分简单了
统共有四种情况：

不能看懂是不是？上图！
zag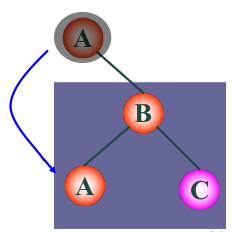

zig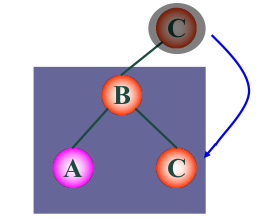

zagzig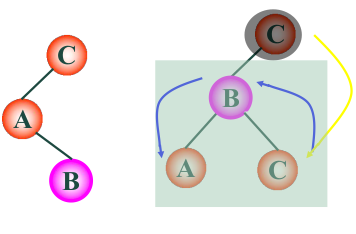

zigzag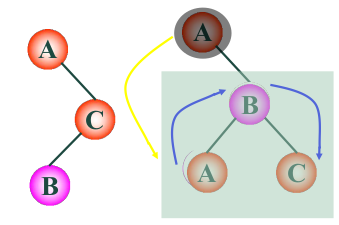

看着麻烦，实际上代码超级简单

int zig(int x){//向右旋
    int y=l[x];
    l[x]=r[y],r[y]=x,up(x),up(y);
    return y;
}
int zag(int x){//向左旋
    int y=r[x];
    r[x]=l[y],l[y]=x,up(x),up(y);
    return y;
}

还有判断应该怎么转的函数

inline void ck(int &x){
    int y;
    if(s[s[x].l].h==s[s[x].r].h+2){//左边较深
        y=s[x].l;
        if(s[s[y].l].h==s[s[x].r].h+1) x=zig(x);//左边的左边较深
        else if(s[s[y].r].h==s[s[x].r].h+1) s[x].l=zag(s[x].l),x=zig(x);//左边的右边较深，
        //把右边较深改到左边较深
    }
    else if(s[s[x].l].h+2==s[s[x].r].h){//右边较深
        y=s[x].r;
        if(s[s[y].r].h==s[s[x].l].h+1) x=zag(x);//右边的右边较深
        else if(s[s[y].l].h==s[s[x].l].h+1) s[x].r=zig(s[x].r),x=zag(x);//右边的左边较深，
        //把左边较深改到右边较深
    }
    up(x);
}

其他操作

既然维护平衡的操作已经没有问题了，其他的操作就其实就跟二叉排序树一样了
这里就把代码贴一下，用来调试

#include<bits/stdc++.h>
using namespace std;
const int N=5e6+10;
int vl[N],h[N],l[N],r[N],sz[N],n,ct;
void up(int x){
    sz[x]=sz[l[x]]+sz[r[x]]+1;
    h[x]=max(h[l[x]],h[r[x]])+1;
}
int zig(int x){int y=l[x];l[x]=r[y],r[y]=x,up(x),up(y);return y;}
int zag(int x){int y=r[x];r[x]=l[y],l[y]=x,up(x),up(y);return y;}
void ck(int &x){
    int y;
    if(h[l[x]]==h[r[x]]+2){
        y=l[x];
        if(h[l[y]]==h[r[x]]+1) x=zig(x);
        else if(h[r[y]]==h[r[x]]+1) l[x]=zag(l[x]),x=zig(x);
    }
    else if(h[l[x]]+2==h[r[x]]){
        y=r[x];
        if(h[r[y]]==h[l[x]]+1) x=zag(x);
        else if(h[l[y]]==h[l[x]]+1) r[x]=zig(r[x]),x=zag(x);
    }
    up(x);
}
void insert(int &x,int y){
    if(x==0){vl[++ct]=y,h[ct]=sz[ct]=1,x=ct;return ;}
    if(y<=vl[x]) insert(l[x],y);
    else insert(r[x],y);
    ck(x);
}
int del(int &x,int y){
    int o;
    if(y==vl[x]||(y>vl[x]&&!r[x])||(y<vl[x]&&!l[x])){
        if(!l[x]||!r[x]){o=vl[x],x=l[x]+r[x];return o;}
        o=vl[x],vl[x]=del(l[x],y);
    }
    else if(y<=vl[x]) o=del(l[x],y);
    else o=del(r[x],y);
    ck(x);
    return o;
}
int kth(int x,int k){
    while(1){
        if(k==sz[l[x]]+1) return x;
        else if(k<=sz[l[x]]) x=l[x];
        else k-=sz[l[x]]+1,x=r[x];
    }
}
int rk(int x,int y){
    int ans=0;
    while(x){
        if(y<=vl[x]) x=l[x];
        else ans+=sz[l[x]]+1,x=r[x];
    }
    return ans+1;
}
int main(){
    int u,v,rt=0;
    scanf("%d",&n);
    while(n--){
        scanf("%d%d",&u,&v);
        if(u==1) insert(rt,v);
        else if(u==2) del(rt,v);
        else if(u==3) printf("%d\n",rk(rt,v));
        else if(u==4) printf("%d\n",vl[kth(rt,v)]);
        else if(u==5) printf("%d\n",vl[kth(rt,rk(rt,v)-1)]);
        else  printf("%d\n",vl[kth(rt,rk(rt,v+1))]);
    }
}

黑科技

其实，在查找严格前驱和严格后继的时候，不必新打一个函数省代码时间到！

因为一个数的排名是这很多个相同的数中最前的那一个，所以这个数的前驱是kth(rank(a)-1)

而后继就是kth（rank（a+1))

总结

初学的时候，看代码量特别大，鸽了很久，但在同学们的帮助下打完之后，感觉其实也不难，核心的思想与代码很容易理解。分区块写，分区块调，一个庞大的程序就出来了。不必怕写不好，只怕不去写。

为其所应为,这样的人才是勇敢的