洛谷 P2046 [NOI2010] 海拔 题解

前置知识

• SPFA
• 网络流
• 平面图转对偶图

分析

尝试贪心之后发现，可以用最小割来解决问题，然而直接套用经典算法发现：TLE！

最大流—最小割定理

定理：在一个网络流中，能够从源点到达汇点的最大流量等于如果从网络中移除就能够导致网络流中断的边的集合的最小容量和。即在任何网络中，最大流的值等于最小割的容量。

证明

定义 $s-t$ 平面图为源点 $s$ 和汇点 $t$ 都在图中无界面的边界上。

已知平面图的性质有：

1. 欧拉公式，一个连通的平面图有 $n$ 个点，$m$ 条边和 $f$ 个面，则 $f=m-n+2$。
2. 每个平面图 $\text{G}$ 都有与其对偶的平面图 $\text{G*}$。

那么，对于 $\text{G}$ 中的每条边 $e$，若它属于两个面 $f_1,f_2$，则加入边 $\operatorname{edge}(f_1^*,f_2^*)$；

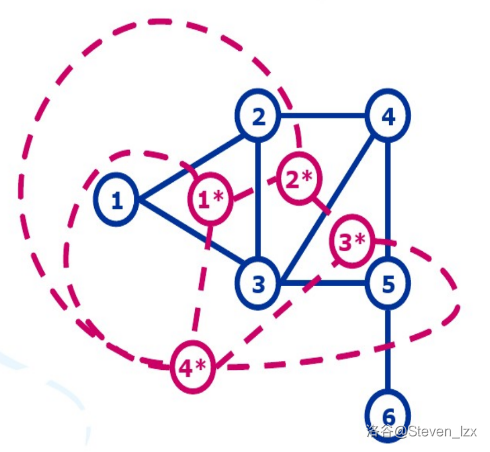
若它只属于一个面 $f$，加入回边 $\operatorname{edge}(f^*,f^*)$。

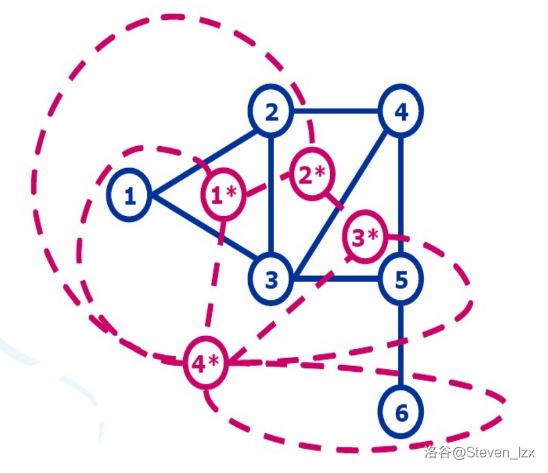
平面图 $\text{G}$ 与其对偶图 $\text{G*}$ 有如下关系：

• $\text{G}$ 的面数等于 $\text{G*}$ 的点数，$\text{G}$ 的点数等于 $\text{G*}$ 的面数，$\text{G}$ 的边数与 $\text{G*}$ 的边数相等。
• $\text{G*}$ 中的环与 $\text{G}$ 中的割一一对应。

应用

直接求解仍然困难，不如利用转化思想，想办法求出最小割。而当长度等于容量时，最小割的容量等于最短路的长度，我们就可以跑最短路来实现了。

实现细节

可以不用建原图，直接在对偶图上跑 SPFA，但 #6 的时间危险，不吸氧（开 O2）可能 TLE。

注意细节（包括但不限于方向）。

Talk is cheap, show me the code. 

namespace LZX
{
    using namespace std;
    typedef long long i64;
    const int MAXN=300005;
    struct Edge
    {
        int to,nxt,w;
    }e[2000005];
    int head[MAXN],cnt=-1,n,v,base,s,t;
    i64 dis[MAXN];
    bool vis[MAXN];
    queue<int> que;
    #define pos(x,y) (~-(x)*base+~-(y))
    void g_addedge(int x,int y,int z)
    {
        e[++cnt].nxt=head[x];
        head[x]=cnt;
        e[cnt].to=y;
        e[cnt].w=z;
        return;
    }
    void g_sp_SPFA()
    {
        int x,y;
        memset(dis,0x3f,sizeof(dis));
        dis[s]=0;
        que.push(s);
        vis[s]=true;
        do
        {
            x=que.front();
            que.pop();
            vis[x]=false;
            for(int i=head[x];~i;i=e[i].nxt)
            {
                y=e[i].to;
                if(dis[y]>dis[x]+e[i].w)
                {
                    dis[y]=dis[x]+e[i].w;
                    if(!vis[y])
                    {
                        que.push(y);
                        vis[y]=true;
                    }
                }
            }
        }
        while(!que.empty());
        return;
    }
    int _main()
    {
        scanf("%d",&n);
        n++;
        base=-~n;
        s=pos(1,base);
        t=pos(base,1);
        memset(head,-1,sizeof(head));
        for(int i=1,j=1;i<=n;j=j%(n-1)+1,i+=(j==1))
        {
            scanf("%d",&v);
            g_addedge(pos(i,j+1),pos(i+1,j+1),v);
        }
        for(int i=1,j=1;i<n;j=j%n+1,i+=(j==1))
        {
            scanf("%d",&v);
            g_addedge(pos(i+1,j+1),pos(i+1,j),v);
        }
        for(int i=1,j=2;i<=n;j=j%n+1,i+=(j==1),j+=(j==1))
        {
            scanf("%d",&v);
            g_addedge(pos(i+1,j),pos(i,j),v);
        }
        for(int i=2,j=1;i<=n;j=j%n+1,i+=(j==1))
        {
            scanf("%d",&v);
            g_addedge(pos(i,j),pos(i,j+1),v);
        }
        for(int i=2;i<base;i++)
        {
            g_addedge(s,pos(1,i),0);
            g_addedge(s,pos(i,base),0);
            g_addedge(pos(i,1),t,0);
            g_addedge(pos(base,i),t,0);
        }
        g_sp_SPFA();
        printf("%lld\n",dis[t]);
        return 0;
    }
}

参考文献：周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》。