最小生成树

最小生成树

关于图的几个概念定义：

• 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。

• 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。

• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

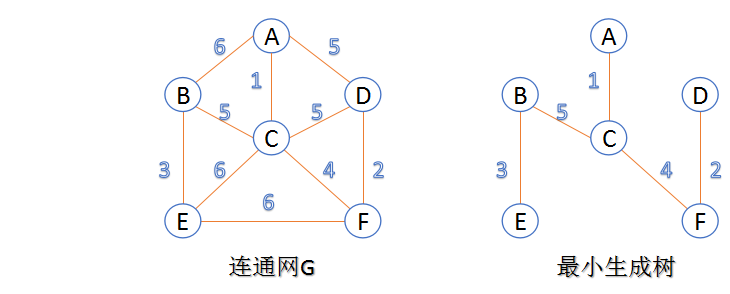
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

1.Kruskal算法

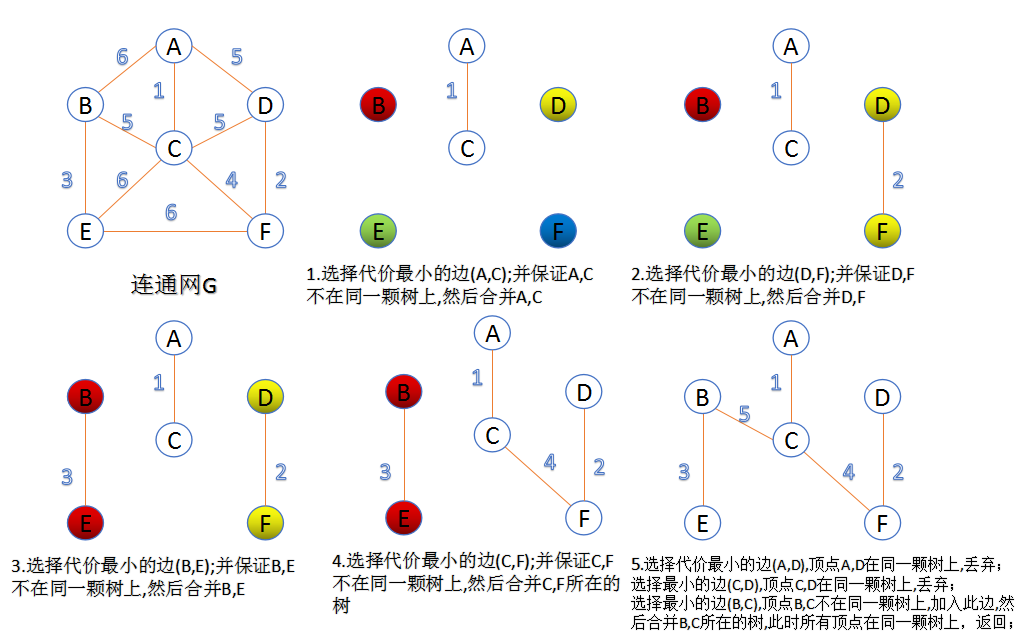
这个方法别称为“加边法”。

1、把所有边按照代价从小到大排序。

2、开始加边。如果这两个顶点不在同一棵树上，则把这两个顶点连接，加入同一棵树上。

如下：

代码如下

#include<bits/stdc++.h>
using namespace std;
int ans,n1,n,head[100005],cnt=1,u1,v1,w1,fa[100005],m,fa1,fa2;
struct Edge
{
    int to,next,w,from;
}edge[200005];
void add_edge(int u,int v,int ww)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].w=ww;
    edge[cnt].next=head[u];
    head[u]=cnt;
    cnt++;
    edge[cnt].from=v;
    edge[cnt].to=u;
    edge[cnt].w=ww;
    edge[cnt].next=head[v];
    head[v]=cnt;
    cnt++;      
}
void qsort(int l,int r)
{
    int i=l,j=r,mid=edge[(l+r)/2].w;
    while(i<=j)
    {
        while(mid>edge[i].w) i++;
        while(mid<edge[j].w) j--;
        if(i<=j)
        {
            swap(edge[i].w,edge[j].w);
            swap(edge[i].next,edge[j].next);
            swap(edge[i].to,edge[j].to);
            swap(edge[i].from,edge[j].from);
            i++;
            j--;
        }
    }
    if(l<j) qsort(l,j);
    if(i<r) qsort(i,r);
}
int f(int x)
{
    if(fa[x]!=x) return f(fa[x]);
    else return x;
}
void in(int x,int y)
{
    fa[f(y)]=f(x);
}
void mst()
{
    n1=n-1;
    for(int i=1;i<=cnt-1;i++)
    {
        if(n1==0) return;
        if(f(edge[i].from)!=f(edge[i].to))
        {
            in(edge[i].from,edge[i].to);
            n1--;
            ans+=edge[i].w;
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&u1,&v1,&w1);
        add_edge(u1,v1,w1);
    }
    for(int i=1;i<=n;i++) fa[i]=i;
    qsort(1,cnt-1);
    mst();
    printf("%d",ans);
    return 0;
}