k-Means聚类

1.基本原理

k-均值聚类实在给定数据集的k个簇的算法。簇的个数是由用户自己定义的，每个簇通过其质心，即簇中所有点的中心。具体工作流程如下：

首先随机确定k个初始点作为质心。然后将数据集中每个点分配到一个簇中，即选择距离该点最近簇中，若簇中有新加入的数据点，则从新计算簇中心。

优点：容易实现

缺点：可能收敛到局部最小值，在大规模数据集中收敛较慢

 2.算法实现：

def loadDataSet(filename):
    dataMat=[]
    fr=open(filename)
    for line in fr.readlines():
        curline=line.strip().split('\t')
        fltline=map(float,curline)
        dataMat.append(list(fltline))
    return dataMat

#计算两个向量距离
def distE(vecA,vecB):
    return sqrt(sum(power(vecA-vecB,2)))

#随机选择中心点
def randCent(dataSet,k):
    n=shape(dataSet)[1]#获取数组列
    centriods=mat(zeros((k,n)))
    for j in range(n):
        minJ=min(dataSet[:,j])#获取每一列数据中最小值
        rangeJ=float(max(array(dataSet)[:,j])-minJ)
        centriods[:,j]=minJ+rangeJ*random.rand(k,1)#随机生成k个数据中心
    return centriods

k-Means核心代码

#dataSet:待聚类数据集
#k待聚类类别
#disMea:距离计算函数
#createCent:随机生成的初始聚类中心
def kmeans(dataSet,k,disMea=distE,createCent=randCent):
    m=shape(dataSet)[0]
    clusterA=mat(zeros((m,2)))#用于存储数据集dataSet中属于k个类别中的哪一类和距该类的距离
    centriods=createCent(dataSet,k)
    clusterC=True
    while clusterC:
        clusterC=False
        for i in range(m):
            minDist=inf
            minIndex=-1
            for j in range(k):
                distJI=disMea(centriods[j,:],dataSet[i,:])#第i个数据集到第j个数据中心距离
                if distJI<minDist:
                    minDist=distJI;minIndex=j
            if clusterA[i,0]!=minIndex:
                clusterC=True
            clusterA[i,:]=minIndex,minDist**2
        print(centriods)
        #遍历聚类类别，跟新聚类中心
        for cent in range(k):
            #nonzero(clusterA[:,0].A==cent获取指定中心的下标，再通过dataSet找到对应的数据
            ptsInClust=dataSet[nonzero(clusterA[:,0].A==cent)[0]]
            centriods[cent,:]=mean(ptsInClust,axis=0)#跟新聚类中心距离
    return centriods,clusterA

可视化

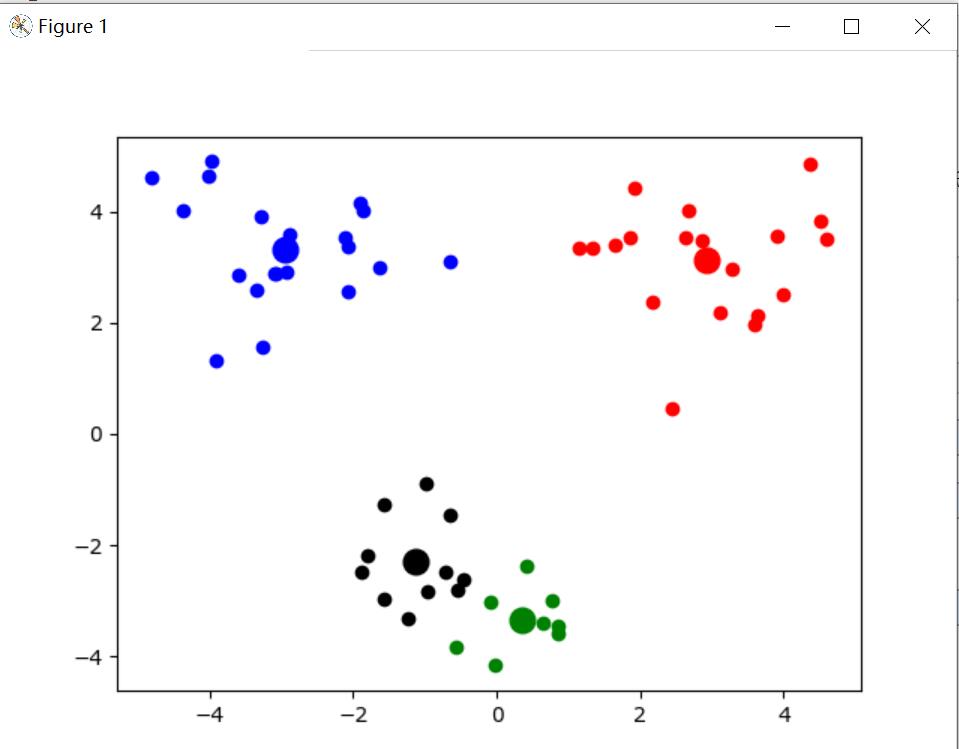
def show(dataSat,k,centriods,clusterA):
    import matplotlib.pyplot as plt
    numSamples,dim=shape(dataSat)
    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
    for i in range(numSamples):
        markIndex=int(clusterA[i,0])
        plt.plot(dataSat[i,0],dataSat[i,1],mark[markIndex])

    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
    for i in range(k):
        plt.plot(centriods[i,0],centriods[i,1],mark[i],markersize=12)
    plt.show()

def main():
    dataMat=mat(loadDataSet('testSet2.txt'))
    myCentroids,clustering=kmeans(dataMat,4)
    print(myCentroids)
    show(dataMat,4,myCentroids,clustering)

if __name__=='__main__':
    main()

3.一种改进的k均值算法----二分k-均值算法

为了克服k均值算法局部收敛问题，有人提出了二分k-均值算法，具体实现：

该算法首先将所有点看作一个簇，然后将该簇一分为二，之后选择其中一个簇继续划分，选择哪一个簇继续划分取决于对其划分是否可以最大程度降低SSE值。

 核心算法如下：

#dataSet:待分类数据集
#k:待分类别
#distMeans:分类距离计算公式
def biKmeans(dataSet,k,distMeans=distE):
    m=shape(dataSet)[0]
    clusterAssment=mat(zeros((m,2)))
    centroid0=mean(dataSet,axis=0).tolist()#按列计算每一列的均值，
    centList=[centroid0]#用于存储每个类中心
    #初始化，将每个数据都看为一个类
    for j in range(m):
        clusterAssment[j,1]=distMeans(mat(centroid0),dataSet[j,:])**2
    while (len(centList)<k):
        lowestSSE=inf
        for i in range(len(centList)):
            ptsInCurrCluster=dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#计算被划分为i类中dataSet所有数据
            centroidMat,splitClustAss=kmeans(ptsInCurrCluster,2,disMea=distMeans)#将ptsInCurrCluster划分为两类
            # print('c',centroidMat)
            sseSplit=sum(splitClustAss[:,1])#计算划分后的均方根（SSE）误差
            sseNotSplit=sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])#计算没有划分数据集均方根误差
            print('sseSplit, and notSplit: ',sseSplit,sseNotSplit)
            #选择误差最小的i类中数据进行划分
            if (sseSplit+sseNotSplit)<lowestSSE:
                bestCentToSplit=i
                bestNewCents=centroidMat
                bestClustAss=splitClustAss.copy()
                lowestSSE=sseNotSplit+sseSplit
        #简单理解就是，我们选择了第i类划分为两类，那么有一类用原来的类编号i，而令一类用centList长度，即将类别加一
        #将二分类数据中划分为1的子类类别变化为centList长度
        print('b',bestClustAss)
        bestClustAss[nonzero(bestClustAss[:,0].A==1)[0],0]=len(centList)
        print('b1',bestClustAss)
        # 将二分类数据中划分为0的子类类别变化为bestCentToSplit
        bestClustAss[nonzero(bestClustAss[:,0].A==0)[0],0]=bestCentToSplit
        print('the bestCentTosplit is :',bestCentToSplit)
        print('the len of bestClustAss is :',len(bestClustAss))
        print('cent',centList)
        #更新用原理类别编号的数据距离
        centList[bestCentToSplit]=bestNewCents[0,:].tolist()
        #新加类别编号len(centList)的距离
        centList.append(bestNewCents[1,:].tolist())
        #将原先分类i中clusterAssment全部数据都变化为bestClustAss
        clusterAssment[nonzero(clusterAssment[:,0].A==bestCentToSplit)[0],:]=bestClustAss
    return centList,clusterAssment