JZOJ 5326. LCA 的统计 (Standard IO)
5326. LCA 的统计 (Standard IO)
Time Limits: 1000 ms Memory Limits: 131072 KB
Description
Input
Output
Sample Input
2 2
1 1
Sample Output
17
Data Constraint
Hint
题解
树形
枚举
有三种情况
1.
2.
3.
把上面三种情况求和,由于
代码
#include<cstdio>
#define mo 1000000007
#define ll long long
#define N 1000010
long fa[N],lc[N],rb[N],next[N],sum[N],ch[N],w[N];
void build(long now)
{
if(!now)return;
build(fa[now]);
ch[fa[now]]+=ch[now];
}
long solve(long now)
{ long ans=0,s1=0,s2=0,i;
for(i=lc[now];i;i=rb[i]){
ans=(ans+solve(i))%mo;
s1=(s1+sum[i])%mo;
}
sum[now]=(sum[now]+s1)%mo;
for(i=lc[now];i;i=rb[i]){
ans=(ans+(ll)(s1-sum[i])*sum[i]%mo*w[now]%mo)%mo;
}
ans=((ll)ans+(ll)w[now]*w[now]%mo*w[now]%mo+2ll*s1%mo*w[now]%mo*w[now]%mo)%mo;
return ans;
}
int main()
{ long n,i;
scanf("%ld%ld",&n,&w[1]);
sum[1]=w[1];
for(i=2;i<=n;i++){
scanf("%ld%ld",&fa[i],&w[i]);
sum[i]=w[i];
ch[fa[i]]++;
if(!lc[fa[i]])
lc[fa[i]]=i;
else
rb[next[fa[i]]]=i;
next[fa[i]]=i;
}
for(i=1;i<=n;i++)
if(!ch[i])
build(i);
printf("%ld\n",solve(1));
return 0;
}

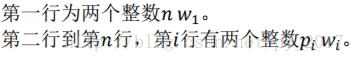

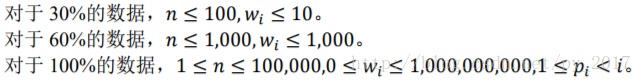
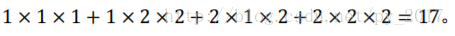

 浙公网安备 33010602011771号
浙公网安备 33010602011771号