20172325 2018-2019-2 《Java程序设计》第七周学习总结
20172325 2018-2019-2 《Java程序设计》第七周学习总结
教材学习内容总结
二叉查找树
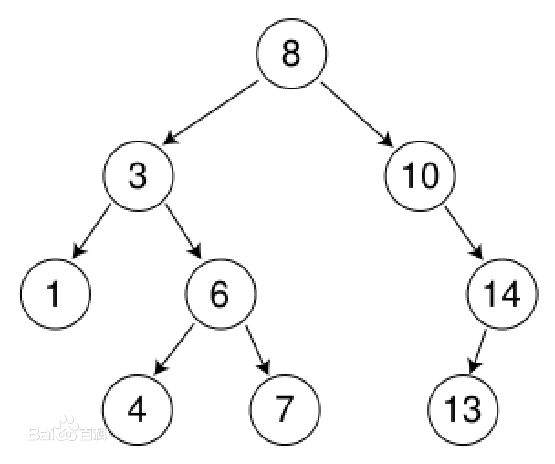
- 二叉查找树:是含附加属性的二叉树,即其左孩子小于父节点,而父节点又小于或等于右孩子。
- 二叉查找树的定义是二叉树定义的扩展。
![]()
- 二叉查找树的各种操作:
addElement:往树中添加一个元素
removeElement:从树中删除一个元素
removeAllOccurrences:从树中删除所指定元素的任何存在
removeMin:删除树中的最小元素
removeMax:删除树中的最大元素
findMin:返回一个指向树中最小元素的引用
findMax:返回一个指向树中最大元素的引用
- 在二叉查找树中:
若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
叶节点的左、右子树也分别为二叉查找树。
没有键值相等的节点。
二叉查找树的删除和插入
-
二叉查找树的插入算法:因为二叉查找树是一个其结点具有特定属性的二叉树所以它的插入算法就只需要一个方法,我二叉查找树与有序列表类似,仅需一个addElement方法就可以把一个元素插入正确的位置。具体的解决方案是:
(1)首先执行查找算法,找出被插结点的父亲结点。
(2)判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。
(3)若二叉树为空。则首先单独生成根结点。 -
二叉查找树的删除算法:删除结点有三种情况分别是需要删除的结点是叶结点,是仅有左子树/右子树的结点,是既有左子树又有右子树的结点。
(1)删除的结点是叶结点,直接让树结点的父结点的下一个指向null即可。
(2)删除的结点是仅有左子树/右子树的结点,将该节点删除后,将该结点的左结点/右结点提到被删除结点的位置即可。
(3)删除的结点是既有左子树又有右子树的结点,这个时候需要用到中序遍历后的前驱结点,将前驱结点提到被删除结点的位置。
addElement操作:就是根据给定元素的值,在树中的恰当位置添加该元素。
如果该元素不是Comparable,该方法会抛出NoComparableElementException异常。
如果树为空,该元素称为新结点。
如果树非空,则依据二叉查找树的性质,分别与某结点及其左右孩子比较,按照左孩子<父节点,父节点<=右孩子的规则将其添加到适当位置,或者称为左右孩子的孩子。
向二叉树中添加元素
removeElement操作:从二叉查找树中删除一个元素时,必须推选出另一个结点(replacement方法找到这个结点)来代替要被删除的那个结点。
在树中找不到给定目标元素时,抛出ElementNotFoundException异常。
选择替换结点的三种情况
被删除结点没有孩子,则replacement返回null
被删除结点只有一个孩子,replacement返回这个孩子
被删除结点有两个孩子,replacement返回中序后继者(因为相等元素会放到右边)
removeAllOccurrences操作:从二叉查找树中删除指定元素的所有存在。
在树中找不到给定目标元素时,抛出ElementNotFoundException异常。
如果该元素不是Comparable,该方法会抛出ClassCastException异常。
该方法会调用一次removeElement方法,以确保当树中根本不存在指定元素时会抛出异常。
如果树中还含有目标元素,就会再次调用removeElement方法。
removeMin操作:据二叉查找树的定义,最右侧存最大的结点,最左侧存最小元素。
如果树根没有左孩子,根结点为最小,右孩子变为新的根结点。
如果左孩子是叶子结点,将父结点的引用设为null即可。
如果左孩子是内部结点,则这个左孩子的右孩子将代替自己成为它父节点的左孩子。
平衡二叉查找树
- 平衡二叉查找树,又称 AVL树。 它除了具备二叉查找树的基本特征之外,还具有一个非常重要的特点:它 的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值(平衡因子 ) 不超过1。 也就是说AVL树每个节点的平衡因子只可能是-1、0和1(左子树高度减去右子树高度)。
- 衡量二叉搜索树搜索效率的标准:平均查找长度(ASL):每个结点比较次数和/结点数
- 平衡因子(BF):左子树的高度减去右子树的高度。
- 判断一个二叉搜索树是否为一个平衡二叉树:|BF|小于等于1当对一个平衡二叉树插入一个结点后,AVL树就变的不平衡了
- 平衡二叉树的调整:分为四种情况
(1)多余点在树的不平衡子树的根结点的右子树的右边:RR插入,需要RR旋转
![]()
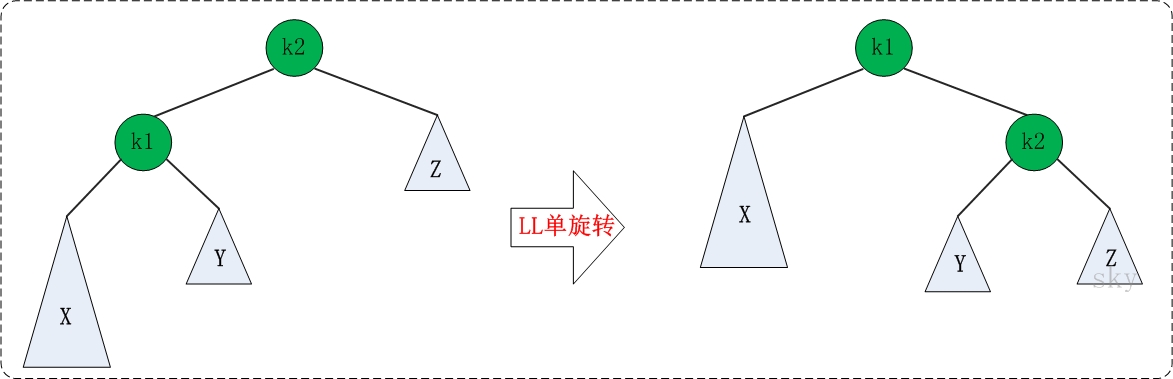
(2)多余点在树的不平衡子树的根结点的左子树的左边:LL插入,需要LL旋转
![]()
(3)多余点在树的不平衡子树的根结点的右子树的左边:RL插入,需要RL旋转
![]()
(4)多余点在树的不平衡子树的根结点的左子树的右边:LR插入,需要LR旋转
![]()
红黑树
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(Null)是黑色。 [注意:这里叶子节点,是指为空(NULL)的叶子节点!]即每个空结点为黑色,也即默认结点为黑色
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

教材学习中的问题和解决过程
-
问题1:如何使二叉查找树在添加数据的同时保持平衡呢?
-
问题1解决方案:当在二叉排序树中插入一个节点时,首先检查是否因插入而破坏了平衡,若 破坏,则找出其中的最小不平衡二叉树,在保持二叉排序树特性的情况下,调整最小不平衡子树中节点之间的关系,以达 到新的平衡。所谓最小不平衡子树 指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树。
-
问题2:红黑树的插入和删除?
-
问题2解决方案:
红黑树的插入,总是把插入的新元素的颜色设为红色,在插入过后极大可能会导致一系列操作以再次平衡红黑树。
红黑树的删除,与插入类似,删除一个元素后有极大可能需要一系列操作以再次平衡红黑树。 -
问题3:二叉查找树、平衡二叉树、红黑树之间的优劣性差异在哪?
-
问题3解决方案:
二叉查找树的操作代价分析:
- (1) 查找代价:
任何一个数据的查找过程都需要从根结点出发,沿某一个路径朝叶子结点前进。因此查找中数据比较次数与树的形态密切相关。
当树中每个结点左右子树高度大致相同时,树高为logN。则平均查找长度与logN成正比,查找的平均时间复杂度在O(logN)数量级上。
当先后插入的关键字有序时,BST退化成单支树结构。此时树高n。平均查找长度为(n+1)/2,查找的平均时间复杂度在O(N)数量级上。 - (2) 插入代价:
新结点插入到树的叶子上,完全不需要改变树中原有结点的组织结构。插入一个结点的代价与查找一个不存在的数据的代价完全相同。 - (3) 删除代价:
当删除一个结点P,首先需要定位到这个结点P,这个过程需要一个查找的代价。然后稍微改变一下树的形态。如果被删除结点的左、右子树只有一个存在,则改变形态的代价仅为O(1)。如果被删除结点的左、右子树均存在,只需要将当P的左孩子的右孩子的右孩子的…的右叶子结点与P互换,在改变一些左右子树即可。因此删除操作的时间复杂度最大不会超过O(logN)。 - BST效率总结 :
查找最好时间复杂度O(logN),最坏时间复杂度O(N)。
插入删除操作算法简单,时间复杂度与查找差不多。
平衡二叉查找树 的操作代价分析:
二叉查找树在最差情况下竟然和顺序查找效率相当,这是无法仍受的。事实也证明,当存储数据足够大的时候,树的结构对某些关键字的查找效率影响很大。当然,造成这种情况的主要原因就是BST不够平衡(左右子树高度差太大)。既然如此,那么我们就需要通过一定的算法,将不平衡树改变成平衡树。因此,AVL树就诞生了。
- (1) 查找代价:
AVL是严格平衡的BST(平衡因子不超过1)。那么查找过程与BST一样,只是AVL不会出现最差情况的BST(单支树)。因此查找效率最好,最坏情况都是O(logN)数量级的。 - (2) 插入代价:
AVL必须要保证严格平衡(|bf|<=1),那么每一次插入数据使得AVL中某些结点的平衡因子超过1就必须进行旋转操作。事实上,AVL的每一次插入结点操作最多只需要旋转1次(单旋转或双旋转)。因此,总体上插入操作的代价仍然在O(logN)级别上(插入结点需要首先查找插入的位置)。 - (3) 删除代价:
AVL删除结点的算法可以参见BST的删除结点,但是删除之后必须检查从删除结点开始到根结点路径上的所有结点的平衡因子。因此删除的代价稍微要大一些。每一次删除操作最多需要O(logN)次旋转。因此,删除操作的时间复杂度为O(logN)+O(logN)=O(2logN) - AVL 效率总结 :
查找的时间复杂度维持在O(logN),不会出现最差情况
AVL树在执行每个插入操作时最多需要1次旋转,其时间复杂度在O(logN)左右。
AVL树在执行删除时代价稍大,执行每个删除操作的时间复杂度需要O(2logN)。
红黑树的操作代价分析:
二叉平衡树的严格平衡策略以牺牲建立查找结构(插入,删除操作)的代价,换来了稳定的O(logN) 的查找时间复杂度。但是这样做是否值得呢?
能不能找一种折中策略,即不牺牲太大的建立查找结构的代价,也能保证稳定高效的查找效率呢? 答案就是:红黑树。
- (1) 查找代价:
由于红黑树的性质(最长路径长度不超过最短路径长度的2倍),可以说明红黑树虽然不像AVL一样是严格平衡的,但平衡性能还是要比BST要好。其查找代价基本维持在O(logN)左右,但在最差情况下(最长路径是最短路径的2倍少1),比AVL要略逊色一点。 - (2) 插入代价:
RBT插入结点时,需要旋转操作和变色操作。但由于只需要保证RBT基本平衡就可以了。因此插入结点最多只需要2次旋转,这一点和AVL的插入操作一样。虽然变色操作需要O(logN),但是变色操作十分简单,代价很小。 - (3) 删除代价:
RBT的删除操作代价要比AVL要好的多,删除一个结点最多只需要3次旋转操作。 - RBT 效率总结 :
查找效率最好情况下时间复杂度为O(logN),但在最坏情况下比AVL要差一些,但也远远好于BST。
插入和删除操作改变树的平衡性的概率要远远小于AVL(RBT不是高度平衡的)。因此需要的旋转操作的可能性要小,而且一旦需要旋转,插入一个结点最多只需要旋转2次,删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN),但是实际上,这种操作由于简单所需要的代价很小。
代码调试中的问题和解决过程
- 问题1:AVL树的左旋、右旋、左右旋、右左旋怎么实现?
- 问题1解决方案:参考蓝墨云资源,发现博客《AVL树(三)之 Java的实现》,试了其中的代码,解决了问题,明白了什么意思。
- 问题2:不会定义红黑树的节点
- 问题2解决方案:查阅了资料,询问了结对伙伴
private static class Node<AnyType>{
Node(AnyType d){
this.data =d;
this.left =null;
this.right =null;
this.parent =null;
this.color =RBTree.BLACK;
}
Node(AnyType d, Node<AnyType> left, Node<AnyType> right,Node<AnyType> parent,boolean color){
this.data =d;
this.left =left;
this.right =right;
this.parent =parent;
this.color =color;
}
AnyType data;
Node<AnyType> left;
Node<AnyType> right;
Node<AnyType> parent;
boolean color;
}
代码托管

(statistics.sh脚本的运行结果截图)
上周考试错题总结
无
结对及互评
- 本周结对学习情况
- 20172306
- 结对学习内容
- 第十一章教材
- 第十一章代码
- 红黑树的相关讨论
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 20/20 | |
| 第二周 | 941/8481 | 1/2 | 18/20 | |
| 第三周 | 653/9134 | 1/3 | 22/20 | |
| 第四周 | 1728/4385 | 2/5 | 8/28 | |
| 第五周 | 933/5318 | 1/6 | 18/20 | |
| 第六周 | 1082/5877 | 1/7 | 20/18 | |
| 第七周 | / | 1/8 | 18/18 |






 浙公网安备 33010602011771号
浙公网安备 33010602011771号