数据结构 第五章 树-类图及代码实现
类图:
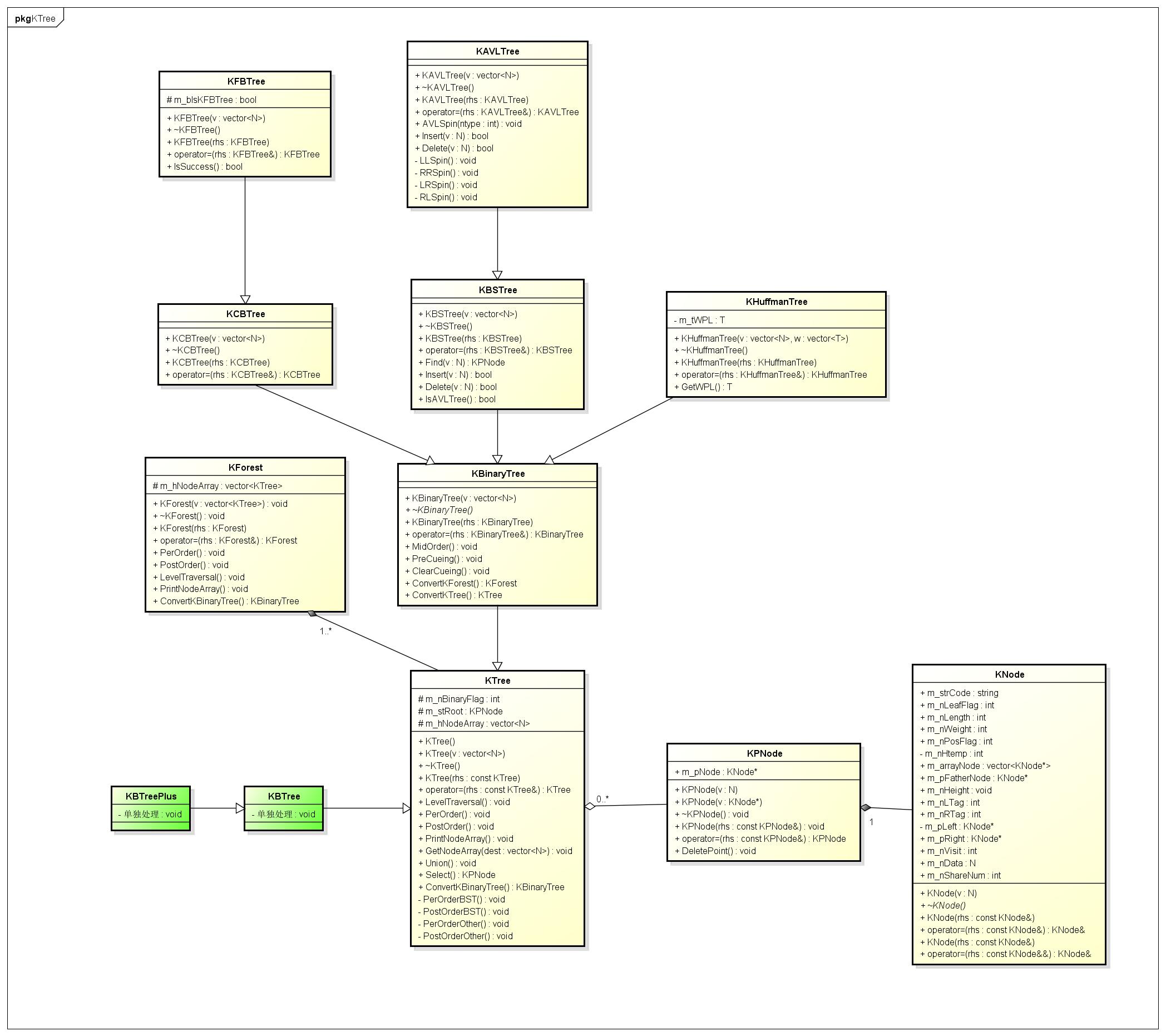
代码实现:
KNode.h
#ifndef DATA_STRUCT_KTREE_K_NODE_H
#define DATA_STRUCT_KTREE_K_NODE_H
// //////////////// 模板类声明与实现都存放在同一个 .h文件中,否则调用会有问题。
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include <stack>
using namespace std;
template<typename N>
class KPNode;
template<typename N>
/**
* 树节点
*/
class KNode
{
public:
/**
* 结点的临时高度 avl树判断时使用
*/
int m_nHtemp;
/**
* 指向其左孩子结点,非二叉树时,值为nullptr
*/
KPNode<N> m_pLeft;
/**
* 前缀编码
*/
string m_strCode;
/**
* 叶结点标志 0-分支结点 1-叶子结点
*/
int m_nLeafFlag;
/**
* 结点的路径长度
*/
int m_nLength;
/**
* 结点的权重
*/
int m_nWeight;
/**
* 结点的位置
* 0-左孩子结点 1-右孩子结点 2-root结点
*/
int m_nPosFlag;
vector<KPNode<N>> m_arrayNode;
/**
* 指向其父结点
*/
KPNode<N> m_pFatherNode;
/**
* 树的高度
*/
int m_nHeight;
/**
* 二叉树线索化时使用,
* 0-left结点指针指向左孩子结点
* 1-left结点指针指向其前驱结点
*
*/
int m_nLTag;
/**
* 二叉树线索化时使用,
* 0-right结点指针指向右孩子结点
* 1-right结点指针指向其后继结点
*/
int m_nRTag;
/**
* 指向其右孩子结点,非二叉树时,值为nullptr
*/
KPNode<N> m_pRight;
/**
* 结点被访问的次数,先序 中序 后序遍历时,出栈判断用
*/
int m_nVisit;
/**
* 结点的值
*/
N m_nData;
/**
* 共享次数,析构时,判断用
*/
int m_nShareNum;
public:
/**
* 构造函数
*/
KNode(N v);
/**
* 析构函数
*/
virtual ~KNode();
/**
* 拷贝构造 注意 &rhs == this 的判断
*/
KNode(const KNode<N>& rhs);
/**
* 拷贝赋值函数
*/
KNode<N>& operator=(const KNode<N>& rhs);
/**
* 移动拷贝构造函数
*/
KNode(const KNode<N>&& rhs);
/**
* 移动赋值函数
*/
KNode<N>& operator=(const KNode<N>&& rhs);
};
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
template<typename N>
KNode<N>::KNode(N v)
{
// 结点的临时高度 avl树判断时使用
m_nHtemp = 1;
// 指向其左孩子结点,非二叉树时,值为nullptr
//m_pLeft = nullptr;
// 叶结点标志 0-分支结点 1-叶子结点
m_nLeafFlag = 0;
// 结点的路径长度
m_nLength = 0;
// 结点的权重
m_nWeight = 0;
// 结点的位置
// 0-左孩子结点 1-右孩子结点 2-root结点
m_nPosFlag = 2;
// 指向其父结点
//m_pFatherNode = nullptr;
// 树的高度
m_nHeight = 1;
/**
* 二叉树线索化时使用,
* 0-left结点指针指向左孩子结点
* 1-left结点指针指向其前驱结点
*/
m_nLTag = 0;
/**
* 二叉树线索化时使用,
* 0-right结点指针指向右孩子结点
* 1-right结点指针指向其后继结点
*/
m_nRTag = 0;
/**
* 指向其右孩子结点,非二叉树时,值为nullptr
*/
//m_pRight = nullptr;
// 结点被访问的次数,先序 中序 后序遍历时,出栈判断用
m_nVisit = 0;
// 结点的值
m_nData = v;
/**
* 共享次数,析构时,判断用
*/
m_nShareNum = 1;
}
template<typename N>
KNode<N>::~KNode()
{
// 关联结点自己释放
cout << m_nData << " ";
}
template<typename N>
KNode<N>::KNode(const KNode<N>& rhs)
{
if (&rhs == this)
{
return;
}
m_nHtemp = rhs.m_nHtemp;
m_pLeft = rhs.m_pLeft;
m_nLeafFlag = rhs.m_nLeafFlag;
m_nLength = rhs.m_nLength;
m_nWeight = rhs.m_nWeight;
m_nPosFlag = rhs.m_nPosFlag;
m_pFatherNode = rhs.m_pFatherNode;
m_nHeight = rhs.m_nHeight;
m_nLTag = rhs.m_nLTag;
m_nRTag = rhs.m_nRTag;
m_pRight = rhs.m_pRight;
m_nVisit = rhs.m_nVisit;
m_nData = rhs.m_nData;
m_nShareNum = ++rhs.m_nShareNum;
}
template<typename N>
KNode<N>& KNode<N>::operator=(const KNode<N>& rhs)
{
if (&rhs != this)
{
m_nHtemp = rhs.m_nHtemp;
m_pLeft = rhs.m_pLeft;
m_nLeafFlag = rhs.m_nLeafFlag;
m_nLength = rhs.m_nLength;
m_nWeight = rhs.m_nWeight;
m_nPosFlag = rhs.m_nPosFlag;
m_pFatherNode = rhs.m_pFatherNode;
m_nHeight = rhs.m_nHeight;
m_nLTag = rhs.m_nLTag;
m_nRTag = rhs.m_nRTag;
m_pRight = rhs.m_pRight;
m_nVisit = rhs.m_nVisit;
m_nData = rhs.m_nData;
m_nShareNum = ++rhs.m_nShareNum;
}
return *this;
}
template<typename N>
KNode<N>::KNode(const KNode<N>&& rhs)
{
if (&rhs != this)
{
m_nHtemp = rhs.m_nHtemp;
m_pLeft = rhs.m_pLeft;
m_nLeafFlag = rhs.m_nLeafFlag;
m_nLength = rhs.m_nLength;
m_nWeight = rhs.m_nWeight;
m_nPosFlag = rhs.m_nPosFlag;
m_pFatherNode = rhs.m_pFatherNode;
m_nHeight = rhs.m_nHeight;
m_nLTag = rhs.m_nLTag;
m_nRTag = rhs.m_nRTag;
m_pRight = rhs.m_pRight;
m_nVisit = rhs.m_nVisit;
m_nData = rhs.m_nData;
m_nShareNum = ++rhs.m_nShareNum;
}
}
template<typename N>
KNode<N>& KNode<N>::operator=(const KNode<N>&& rhs)
{
if (&rhs != this)
{
m_nHtemp = rhs.m_nHtemp;
m_pLeft = rhs.m_pLeft;
m_nLeafFlag = rhs.m_nLeafFlag;
m_nLength = rhs.m_nLength;
m_nWeight = rhs.m_nWeight;
m_nPosFlag = rhs.m_nPosFlag;
m_pFatherNode = rhs.m_pFatherNode;
m_nHeight = rhs.m_nHeight;
m_nLTag = rhs.m_nLTag;
m_nRTag = rhs.m_nRTag;
m_pRight = rhs.m_pRight;
m_nVisit = rhs.m_nVisit;
m_nData = rhs.m_nData;
m_nShareNum = ++rhs.m_nShareNum;
}
return *this;
}
#endif
KPNode.h
#ifndef DATA_STRUCT_KTREE_K_P_NODE_H
#define DATA_STRUCT_KTREE_K_P_NODE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KNode.h"
template<typename N>
struct compare {
bool operator() (const KPNode<N> &lhs, const KPNode<N> &rhs) const{
return (lhs.m_pNode->m_nWeight > rhs.m_pNode->m_nWeight);
}
};
template<typename N>
/**
* 包含树节点指针的类,构造哈夫曼树是,放到set 结点中,只复制指针,提高效率
*/
class KPNode
{
public:
KNode<N>* m_pNode;
public:
KPNode();
KPNode(N v);
KPNode(KNode<N>* v);
/**
* 析构时,不释放m_pNode指针,由外层的调用 DeletePoint()函数来释放
*/
virtual ~KPNode();
KPNode(const KPNode<N>& rhs);
KPNode<N>& operator=(const KPNode<N>& rhs);
/**
* 释放 m_pNode 结点
*/
void DeletePoint();
bool operator<(const KPNode<N>& tmp) const{
if (this->m_pNode->m_nWeight < tmp.m_pNode->m_nWeight)
return true; //自定义排序规则
return false;
}
};
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
template<typename N>
KPNode<N>::KPNode()
{
m_pNode = nullptr;
}
template<typename N>
KPNode<N>::KPNode(N v)
{
//m_pNode = nullptr;
m_pNode = new (std::nothrow) KNode<N>(v);
}
template<typename N>
KPNode<N>::KPNode(KNode<N>* v)
{
//if (m_pNode != v && nullptr != m_pNode)
//{
// DeletePoint();
//}
// v->m_nShareNum++;
m_pNode = v;
}
template<typename N>
KPNode<N>::~KPNode()
{
// DeletePoint();
// m_pNode = nullptr;
}
template<typename N>
KPNode<N>::KPNode(const KPNode<N>& rhs)
{
if (&rhs != this)
{
m_pNode = rhs.m_pNode;
// m_pNode->m_nShareNum++;
}
}
template<typename N>
KPNode<N>& KPNode<N>::operator=(const KPNode<N>& rhs)
{
if (&rhs != this)
{
m_pNode = rhs.m_pNode;
// m_pNode->m_nShareNum++;
}
return *this;
}
template<typename N>
void KPNode<N>::DeletePoint()
{
//if (nullptr == m_pNode)
//{
// return;
//}
// int k = m_pNode->m_arrayNode.size();
// if (nullptr != m_pNode->m_pLeft.m_pNode)
// {
// k++;
// }
// if (nullptr != m_pNode->m_pRight.m_pNode)
// {
// k++;
// }
//
// // 引用计数减一
//// m_pNode->m_nShareNum--;
// if (m_pNode->m_nShareNum == k)
// {
// delete m_pNode;
// m_pNode = nullptr;
// }
delete m_pNode;
m_pNode = nullptr;
}
#endif
KTree.h
#ifndef DATA_STRUCT_KTREE_K_TREE_H
#define DATA_STRUCT_KTREE_K_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KPNode.h"
//#include "../KTree/KBinaryTree.h"
template<typename N>
class KBinaryTree;
template<typename N>
/**
* 普通树
*/
class KTree
{
protected:
/**
* 0 普通树 1-二叉树
*/
int m_nBinaryFlag;
/**
* 根结点
*/
KPNode<N> m_stRoot;
/**
* 保存遍历后的结果结点
*/
vector<KPNode<N>> m_hNodeArray;
/*
/ **
* 共享次数,析构时,判断用
* /
int m_nShareNum;*/
protected:
/**
* 二叉树的先序遍历
*/
void PerOrderBST();
/**
* 二叉树的后序遍历
*/
void PostOrderBST();
/**
* 非二叉树的先序遍历
*/
void PerOrderOther();
/**
* 非二叉树的后序遍历
*/
void PostOrderOther();
// 二叉树的层次遍历
void LevelTraversalBST();
// 普通树的层次遍历
void LevelTraversalOther();
// 构造树
void CreateKTree(vector<N> v, vector<int> level_num)
{
if (v.size() > 0)
{
m_stRoot = KPNode<N>(v[0]);
m_stRoot.m_pNode->m_nPosFlag = 2;
}
// 开始构建树
// 使用队列,对结点进行赋值操作
queue<KPNode<N>> temp_queue;
temp_queue.push(m_stRoot);
int i = 1;
// 结点数量
for (auto num : level_num)
{
if (temp_queue.empty())
{
break;
}
KPNode<N> node = temp_queue.front();
temp_queue.pop();
for (int j = 0; j < num && i < (int)v.size(); i++, j++)
{
KPNode<N> new_node = KPNode<N>(v[i]);
node.m_pNode->m_arrayNode.push_back(new_node.m_pNode);
new_node.m_pNode->m_pFatherNode = node.m_pNode;
temp_queue.push(new_node);
}
}
}
// 删除原树结点
void delete_point()
{
if (nullptr == m_stRoot.m_pNode)
{
return;
}
m_stRoot.m_pNode->m_nShareNum--;
if (0 == m_stRoot.m_pNode->m_nShareNum)
{
cout << "delete tree:";
// 树进行层次遍历
LevelTraversal();
// 释放节点
for (auto v : m_hNodeArray)
{
//v.m_pNode->m_nShareNum = 2;
v.DeletePoint();
}
cout << endl;
}
}
public:
/**
* 默认构造函数
*/
KTree();
//{
// m_nBinaryFlag = 0;
// m_stRoot = nullptr;
//}
KTree(KPNode<N>& n){
m_stRoot = n;
m_stRoot.m_pNode->m_nShareNum++;
}
/**
* 构造函数
* vector<int> level_num 按层次,从左到右后,续结点的个数
*/
KTree(vector<N> v, vector<int> level_num);
/**
* 析构函数
*/
virtual ~KTree();
/**
* 拷贝构造
*/
KTree(const KTree<N>& rhs);
/**
* 拷贝赋值函数
*/
KTree operator=(const KTree<N>& rhs);
/**
* 树的层次遍历
*/
void LevelTraversal();
/**
* 先根/先序遍历
*/
void PerOrder();
/**
* 后序遍历
*/
void PostOrder();
/**
* 打印 保存遍历结果的结点数组
*/
void PrintNodeArray();
/**
* 取得打印结果数组
*/
void GetNodeArray(vector<N>& dest);
/**
* 树的并查集之并操作
*/
void Union(KTree<N>& rhs);
/**
* 树的并查集之查操作
*/
KPNode<N> Select();
/**
* 转换为二叉树 true 成功 false 失败
*/
KBinaryTree<N> ConvertKBinaryTree();
};
//#include "../KTree/KTree.cpp"
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <queue>
#include <assert.h>
//#include "KTree.h"
//#include "KBinaryTree.h"
//template<typename N>
//class KBinaryTree;
template<typename N>
KTree<N>::KTree()
{
m_nBinaryFlag = 0;
//m_stRoot = nullptr;
//m_nShareNum = 1;
}
template<typename N>
KTree<N>::KTree(vector<N> v, vector<int> level_num)
{
m_nBinaryFlag = 0;
// 创建树
CreateKTree(v, level_num);
}
template<typename N>
KTree<N>::~KTree()
{
//int k = m_stRoot.m_pNode->m_arrayNode.size();
//if (nullptr != m_stRoot.m_pNode->m_pLeft.m_pNode)
//{
// k++;
//}
//if (nullptr != m_stRoot.m_pNode->m_pRight.m_pNode)
//{
// k++;
//}
//m_hNodeArray.clear();
if (nullptr == m_stRoot.m_pNode)
{
return;
}
m_stRoot.m_pNode->m_nShareNum--;
if (0 == m_stRoot.m_pNode->m_nShareNum)
{
cout << "delete tree:";
// 树进行层次遍历
LevelTraversal();
// 释放节点
for (auto v : m_hNodeArray)
{
//v.m_pNode->m_nShareNum = 2;
v.DeletePoint();
}
cout << endl;
}
}
template<typename N>
KTree<N>::KTree(const KTree<N>& rhs)
{
// m_nBinaryFlag = 0;
if (&rhs != this)
{
delete_point();
m_stRoot = rhs.m_stRoot;
m_stRoot.m_pNode->m_nShareNum++;
}
}
template<typename N>
KTree<N> KTree<N>::operator=(const KTree<N>& rhs)
{
// m_nBinaryFlag = 0;
if (&rhs != this)
{
delete_point();
m_stRoot = rhs.m_stRoot;
m_stRoot.m_pNode->m_nShareNum++;
}
return *this;
}
template<typename N>
void KTree<N>::LevelTraversal()
{
m_hNodeArray.clear();
if (0 == m_nBinaryFlag)
{
LevelTraversalOther();
}
else
{
LevelTraversalBST();
}
}
template<typename N>
void KTree<N>::PerOrder()
{
m_hNodeArray.clear();
if (0 == m_nBinaryFlag)
{
PerOrderOther();
}
else
{
PerOrderBST();
}
}
template<typename N>
void KTree<N>::PostOrder()
{
m_hNodeArray.clear();
if (0 == m_nBinaryFlag)
{
PostOrderOther();
}
else
{
PostOrderBST();
}
}
template<typename N>
void KTree<N>::PrintNodeArray()
{
cout << "m_nData:" << endl;
for (auto v : m_hNodeArray)
{
cout << v.m_pNode->m_nData << '\t';
}
cout << endl;
cout << "m_strCode:" << endl;
for (auto v : m_hNodeArray)
{
cout << v.m_pNode->m_strCode << '\t';
}
cout << endl;
cout << "m_nLength:" << endl;
for (auto v : m_hNodeArray)
{
cout << v.m_pNode->m_nLength << '\t';
}
cout << endl;
cout << "m_nWeight:" << endl;
for (auto v : m_hNodeArray)
{
cout << v.m_pNode->m_nWeight << '\t';
}
cout << endl;
}
template<typename N>
void KTree<N>::GetNodeArray(vector<N>& dest)
{
dest.clear();
for (auto v : m_hNodeArray)
{
dest.push_back(v.m_pNode->m_nData);
}
}
template<typename N>
void KTree<N>::Union(KTree<N>& rhs)
{
rhs.m_stRoot.m_pNode->m_pFatherNode = m_stRoot.m_pNode;
rhs.m_stRoot.m_pNode->m_nPosFlag = 0;
m_stRoot.m_pNode->m_arrayNode.push_back(rhs.m_stRoot.m_pNode);
//delete rhs.m_stRoot;
m_stRoot.m_pNode->m_nShareNum += rhs.m_stRoot.m_pNode->m_nShareNum;
rhs.m_stRoot = m_stRoot;
}
template<typename N>
KPNode<N> KTree<N>::Select()
{
return m_stRoot;
}
// 树 转 二叉树
template<typename N>
KBinaryTree<N> KTree<N>::ConvertKBinaryTree()
{
//if (1 == m_nBinaryFlag)
//{
// return *this;
//}
m_nBinaryFlag = 1;
KBinaryTree<N> bintree;
auto T = m_stRoot.m_pNode;
if (T == nullptr)
{
return bintree;
}
//m_stRoot.m_pNode->m_nShareNum++;
queue<KPNode<N>> node_queue;
node_queue.push(m_stRoot);
while (!node_queue.empty())
{
auto K = node_queue.front();
node_queue.pop();
if (K.m_pNode->m_arrayNode.size() == 0)
{
continue;
}
// 左结点
K.m_pNode->m_pLeft = K.m_pNode->m_arrayNode[0];
K.m_pNode->m_arrayNode[0].m_pNode->m_pFatherNode = K.m_pNode;
K.m_pNode->m_arrayNode[0].m_pNode->m_nPosFlag = 0;
node_queue.push(K.m_pNode->m_arrayNode[0]);
size_t i = 1;
// 右结点
for (; i< K.m_pNode->m_arrayNode.size(); i++)
{
K.m_pNode->m_arrayNode[i - 1].m_pNode->m_pRight = K.m_pNode->m_arrayNode[i];
K.m_pNode->m_arrayNode[i].m_pNode->m_pFatherNode = K.m_pNode->m_arrayNode[i - 1];
K.m_pNode->m_arrayNode[i].m_pNode->m_nPosFlag = 1;
node_queue.push(K.m_pNode->m_arrayNode[i]);
}
K.m_pNode->m_arrayNode.clear();
}
return KBinaryTree<N>(m_stRoot);
}
template<typename N>
void KTree<N>::PerOrderBST()
{
if (m_stRoot.m_pNode == nullptr)
{
return ;
}
stack<KPNode<N>> node_stack;
node_stack.push(m_stRoot);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
m_hNodeArray.push_back(K);
// 右子树入栈
if (nullptr != K.m_pNode->m_pRight.m_pNode)
{
node_stack.push(K.m_pNode->m_pRight);
}
// 左子树入栈
if (nullptr != K.m_pNode->m_pLeft.m_pNode)
{
node_stack.push(K.m_pNode->m_pLeft);
}
}
}
template<typename N>
void KTree<N>::PostOrderBST()
{
if (m_stRoot.m_pNode == nullptr)
{
return;
}
stack<KPNode<N>> node_stack;
node_stack.push(m_stRoot);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
if (K.m_pNode->m_nVisit == 2)
{
if (nullptr != K.m_pNode->m_pFatherNode.m_pNode)
{
K.m_pNode->m_pFatherNode.m_pNode->m_nVisit++;
}
m_hNodeArray.push_back(K);
K.m_pNode->m_nVisit = 0;
continue;
}
node_stack.push(K);
// 右结点入栈
if (nullptr != K.m_pNode->m_pRight.m_pNode)
{
node_stack.push(K.m_pNode->m_pRight.m_pNode);
}
else
{
K.m_pNode->m_nVisit++;
}
// 左结点入栈
if (nullptr != K.m_pNode->m_pLeft.m_pNode)
{
node_stack.push(K.m_pNode->m_pLeft.m_pNode);
}
else
{
K.m_pNode->m_nVisit++;
}
}
}
template<typename N>
void KTree<N>::PerOrderOther()
{
if (m_stRoot.m_pNode == nullptr)
{
return;
}
stack<KPNode<N>> node_stack;
node_stack.push(m_stRoot);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
m_hNodeArray.push_back(K);
// 子树逆序入栈
for (int i = K.m_pNode->m_arrayNode.size() - 1; i >= 0; i--)
{
node_stack.push(K.m_pNode->m_arrayNode[i]);
}
}
}
template<typename N>
void KTree<N>::PostOrderOther()
{
if (m_stRoot.m_pNode == nullptr)
{
return;
}
stack<KPNode<N>> node_stack;
node_stack.push(m_stRoot);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
if (K.m_pNode->m_arrayNode.size() == 0 || K.m_pNode->m_nVisit > 0)
{
m_hNodeArray.push_back(K);
continue;
}
K.m_pNode->m_nVisit++;
node_stack.push(K);
// 子树逆序入栈
for (int i = K.m_pNode->m_arrayNode.size() - 1; i >= 0; i--)
{
node_stack.push(K.m_pNode->m_arrayNode[i]);
}
}
}
template<typename N>
void KTree<N>::LevelTraversalBST()
{
if (nullptr == m_stRoot.m_pNode)
{
return;
}
queue<KPNode<N>> node_queue;
node_queue.push(m_stRoot);
while (!node_queue.empty())
{
KPNode<N> K = node_queue.front();
node_queue.pop();
m_hNodeArray.push_back(K);
if (K.m_pNode->m_pLeft.m_pNode != nullptr && K.m_pNode->m_nLTag == 0)
{
node_queue.push(K.m_pNode->m_pLeft.m_pNode);
}
if (K.m_pNode->m_pRight.m_pNode != nullptr && K.m_pNode->m_nRTag == 0)
{
node_queue.push(K.m_pNode->m_pRight.m_pNode);
}
}
}
template<typename N>
void KTree<N>::LevelTraversalOther()
{
if (nullptr == m_stRoot.m_pNode)
{
return;
}
queue<KPNode<N>> node_queue;
node_queue.push(m_stRoot);
while (!node_queue.empty())
{
KPNode<N> K = node_queue.front();
node_queue.pop();
m_hNodeArray.push_back(K); // 保存扫描队列
if (K.m_pNode->m_arrayNode.size() == 0)
{
continue;
}
for (auto v : K.m_pNode->m_arrayNode)
{
node_queue.push(v);
}
}
}
#endif
KBinaryTree.h
#ifndef DATA_STRUCT_KTREE_K_BINARY_TREE_H
#define DATA_STRUCT_KTREE_K_BINARY_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KTree.h"
template<typename N>
class KForest;
template<typename N>
/**
* 二叉树
*/
class KBinaryTree : public KTree<N>
{
public:
// 默认构造函数
KBinaryTree(){ m_nBinaryFlag = 1; }
// 默认构造函数
KBinaryTree(KPNode<N>& t) :KTree(t){ m_nBinaryFlag = 1; }
/**
* 构造函数
* pos_flag 0-左孩子结点 1-右孩子结点 2-root结点
*/
KBinaryTree(vector<N> v, vector<int> level_num, vector<int> pos_flag)
{
m_nBinaryFlag = 1;
// 判断分支
for (auto& v : level_num)
{
if (v > 2)
{
return;
}
}
// 根结点创建
if (v.size() == 0)
{
return;
}
m_stRoot = KPNode<N>(v[0]);
m_stRoot.m_pNode->m_nPosFlag = 2;
// 其他结点创建
// 使用队列,对结点进行赋值操作
queue<KPNode<N>> temp_queue;
temp_queue.push(m_stRoot);
int i = 1;
// 结点数量
for (auto num : level_num)
{
if (temp_queue.empty())
{
break;
}
KPNode<N> node = temp_queue.front();
temp_queue.pop();
for (int j = 0; j < num && i < (int)v.size(); i++, j++)
{
KPNode<N> new_node = KPNode<N>(v[i]);
if (0 == pos_flag[i])
{
node.m_pNode->m_pLeft = new_node;
}
else
{
node.m_pNode->m_pRight = new_node;
}
new_node.m_pNode->m_pFatherNode = node.m_pNode;
temp_queue.push(new_node);
}
}
}
/**
* 析构函数
*/
virtual ~KBinaryTree()
{
}
/**
* 拷贝构造函数
*/
KBinaryTree(KBinaryTree<N>& rhs)
:KTree(rhs)
{
// m_nBinaryFlag = 1;
}
/**
* 赋值函数
*/
KBinaryTree operator=(KBinaryTree<N>& rhs)
{
if (this == &rhs) return *this;
// 调用基类的 赋值构造函数
KTree::operator=(rhs);
// m_nBinaryFlag = 1;
return *this;
}
// 左结点追加子树
void AddChildTreeForRight(KBinaryTree<N>& rhs)
{
rhs.m_stRoot.m_pNode->m_nPosFlag = 1;;
rhs.m_stRoot.m_pNode->m_nShareNum++;
rhs.m_stRoot.m_pNode->m_pFatherNode = m_stRoot;
m_stRoot.m_pNode->m_pRight = rhs.m_stRoot;
}
/**
* 中序遍历
*/
void MidOrder()
{
m_hNodeArray.clear();
if (m_stRoot.m_pNode == nullptr)
{
return;
}
stack<KPNode<N>> node_stack;
node_stack.push(m_stRoot);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
if (K.m_pNode->m_nVisit == 1)
{
if (nullptr != K.m_pNode->m_pFatherNode.m_pNode)
{
K.m_pNode->m_pFatherNode.m_pNode->m_nVisit++;
}
m_hNodeArray.push_back(K);
K.m_pNode->m_nVisit = 0;
continue;
}
// 右结点入栈
if (nullptr != K.m_pNode->m_pRight.m_pNode)
{
node_stack.push(K.m_pNode->m_pRight.m_pNode);
}
// 父结点入栈
node_stack.push(K);
// 左结点入栈
if (nullptr != K.m_pNode->m_pLeft.m_pNode)
{
node_stack.push(K.m_pNode->m_pLeft.m_pNode);
}
else
{
K.m_pNode->m_nVisit++;
}
}
}
/**
* 先序线索化,按照先序遍历,把树结点链式化,中序、后序
*/
void PreCueing()
{
// 先序遍历
PerOrder();
// 清理线索化
ClearCueing();
// 先序线索化
for (size_t i = 1; i < m_hNodeArray.size()-1; i++)
{
// 前驱节点
if (nullptr == m_hNodeArray[i].m_pNode->m_pLeft.m_pNode)
{
m_hNodeArray[i].m_pNode->m_nLTag = 1;
m_hNodeArray[i].m_pNode->m_pLeft.m_pNode = m_hNodeArray[i - 1].m_pNode;
}
// 后继节点
if (nullptr == m_hNodeArray[i].m_pNode->m_pRight.m_pNode)
{
m_hNodeArray[i].m_pNode->m_nRTag = 1;
m_hNodeArray[i].m_pNode->m_pRight.m_pNode = m_hNodeArray[i+1].m_pNode;
}
}
// 先序线索化 打印结果
cout << "先序线索化的结果: " << endl;
for (size_t i = 1; i < m_hNodeArray.size() - 1; i++)
{
// 前驱节点
if (1 == m_hNodeArray[i].m_pNode->m_nLTag)
{
cout << m_hNodeArray[i].m_pNode->m_nData << " 的前驱结点为:\t" << m_hNodeArray[i].m_pNode->m_pLeft.m_pNode->m_nData << endl;
}
// 后继节点
if (1 == m_hNodeArray[i].m_pNode->m_nRTag)
{
cout << m_hNodeArray[i].m_pNode->m_nData << " 的后继结点为:\t" << m_hNodeArray[i].m_pNode->m_pRight.m_pNode->m_nData << endl;
}
}
}
/**
* 清理线索化
*/
void ClearCueing()
{
for (auto v : m_hNodeArray)
{
if (1 == v.m_pNode->m_nLTag)
{
v.m_pNode->m_pLeft.m_pNode = nullptr;
v.m_pNode->m_nLTag = 0;
}
if (1 == v.m_pNode->m_nRTag)
{
v.m_pNode->m_pRight.m_pNode = nullptr;
v.m_pNode->m_nLTag = 0;
}
}
}
/**
* 二叉树转森林 true 成功 false 失败
*/
bool ConvertKForest(KForest<N>& hKForest)
{
if (nullptr == m_stRoot.m_pNode)
{
return false;
}
vector<KTree<N>> KTreeArray;
auto K = m_stRoot;
auto temp_right = K.m_pNode->m_pRight;
K.m_pNode->m_pRight.m_pNode = nullptr;
//KTreeArray.push_back(K);
auto temp = KBinaryTree<N>(K);
KTreeArray.push_back(temp);
while (nullptr != temp_right.m_pNode)
{
K = temp_right;
temp_right = K.m_pNode->m_pRight;
K.m_pNode->m_pRight.m_pNode = nullptr;
temp = KBinaryTree<N>(K);
KTreeArray.push_back(temp);
}
//for (auto& v : KTreeArray)
//{
// v.m_nBinaryFlag = 1;
//}
hKForest = KForest<N>(KTreeArray);
return true;
}
/**
* 二叉树转普通树 true 成功 false 失败
*/
bool ConvertKTree(KTree<N>& Tree)
{
if (0 == m_nBinaryFlag)
{
return true;
}
if (nullptr == m_stRoot.m_pNode)
{
m_nBinaryFlag = 0;
Tree = *this;
return true;
}
// 该树只能转换为森林
if (nullptr != m_stRoot.m_pNode->m_pRight.m_pNode)
{
return false;
}
if (nullptr == m_stRoot.m_pNode->m_pLeft.m_pNode)
{
m_nBinaryFlag = 0;
Tree = *this;
return true;
}
queue<KPNode<N>> node_queue;
node_queue.push(m_stRoot.m_pNode->m_pLeft);
while (!node_queue.empty())
{
auto K = node_queue.front();
node_queue.pop();
auto F = K.m_pNode->m_pFatherNode;
auto temp = K;
auto R = temp.m_pNode->m_pRight;
temp.m_pNode->m_pRight = nullptr;
auto& node_array = F.m_pNode->m_arrayNode;
node_array.clear();
node_array.push_back(K);
F.m_pNode->m_pLeft = nullptr;
while (true)
{
if (nullptr != temp.m_pNode->m_pLeft.m_pNode)
{
node_queue.push(temp.m_pNode->m_pLeft);
}
if (nullptr == R.m_pNode)
{
break;
}
node_array.push_back(R);
R.m_pNode->m_pFatherNode = F;
temp = R;
R = R.m_pNode->m_pRight;
temp.m_pNode->m_pRight = nullptr;
}
}
m_nBinaryFlag = 0;
Tree = *this;
return true;
}
};
#endif
KForest.h
#ifndef DATA_STRUCT_KTREE_K_FOREST_H
#define DATA_STRUCT_KTREE_K_FOREST_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KTree.h"
#include "../KTree/KBinaryTree.h"
template<typename N>
/**
* 森林
*/
class KForest
{
protected:
/**
* 森林遍历结果的保存值
*/
vector<KTree<N>> m_hTreeArray;
public:
/**
* 构造函数
*/
KForest()
{
}
KForest(vector<KTree<N>> v)
{
m_hTreeArray = v;
}
/**
* 析构函数
*/
~KForest()
{
}
/**
* 拷贝构造函数
*/
KForest(const KForest<N>& rhs)
{
this->m_hTreeArray = rhs.m_hTreeArray;
}
/**
* 赋值函数
*/
KForest operator=(const KForest<N>& rhs)
{
if (this != &rhs)
{
this->m_hTreeArray = rhs.m_hTreeArray;
}
return *this;
}
/**
* 先序遍历
*/
void PerOrder()
{
for (auto& v : m_hTreeArray)
{
v.PerOrder();
}
}
/**
* 后序遍历
*/
void PostOrder()
{
for (auto& v : m_hTreeArray)
{
v.PostOrder();
}
}
/**
* 层次遍历
*/
void LevelTraversal()
{
for (auto& v : m_hTreeArray)
{
v.LevelTraversal();
}
}
/**
* 打印遍历结果
*/
void PrintNodeArray()
{
for (auto& v : m_hTreeArray)
{
v.PrintNodeArray();
}
}
/**
* 转换为二叉树 true 成功 false 失败
*/
KBinaryTree<N> ConvertKBinaryTree()
{
//KPNode root;
vector<KBinaryTree<N>> KBinaryTreeArray;
for (auto& v : m_hTreeArray)
{
KBinaryTreeArray.push_back(v.ConvertKBinaryTree());
}
// 二叉树组合
for (size_t i = 1; i < KBinaryTreeArray.size(); i++)
{
KBinaryTreeArray[i - 1].AddChildTreeForRight(KBinaryTreeArray[i]);
}
if (KBinaryTreeArray.size() > 0)
{
return KBinaryTreeArray[0];
}
return KBinaryTree<N>();
}
};
#endif
KBSTree.h
#ifndef DATA_STRUCT_KTREE_K_B_S_TREE_H
#define DATA_STRUCT_KTREE_K_B_S_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KBinaryTree.h"
#include "../KTree/KPNode.h"
template<typename N>
/**
* 二叉排序树/二叉查找树
*/
class KBSTree : public KBinaryTree<N>
{
protected:
KPNode<N> m_stpNotAVLNode; // 非AVL树的起始节点
public:
/**
* 构造函数
*/
KBSTree()
{
}
/**
* 构造函数
*/
KBSTree(vector<N> v)
{
for (auto n:v)
{
Insert(n);
}
}
/**
* 析构函数
*/
~KBSTree()
{
}
/**
* 拷贝构造函数
*/
KBSTree(KBSTree<N>& rhs)
:KBinaryTree(rhs)
{
}
/**
* 赋值函数
*/
KBSTree operator=(KBSTree<N>& rhs)
{
KBinaryTree::operator=(rhs);
}
/**
* 查找结点
*/
KPNode<N> Find(N v)
{
KPNode<N> ret;
auto T = m_stRoot;
while (true)
{
if (nullptr == T.m_pNode)
{
break;
}
if (v < T.m_pNode->m_nData)
{
T = T.m_pNode->m_pLeft;
continue;
}
if (v > T.m_pNode->m_nData)
{
T = T.m_pNode->m_pRight;
continue;
}
ret = T;
break;
}
return ret;
}
// 插入结点
virtual bool Insert(N v)
{
KPNode<N> NewNode(v);
if (nullptr == m_stRoot.m_pNode)
{
m_stRoot = NewNode;
m_stRoot.m_pNode->m_nPosFlag = 2;
return true;
}
auto T = m_stRoot;
while (true)
{
if (v < T.m_pNode->m_nData)
{
if (nullptr == T.m_pNode->m_pLeft.m_pNode)
{
NewNode.m_pNode->m_nPosFlag = 0;
NewNode.m_pNode->m_pFatherNode = T;
T.m_pNode->m_pLeft = NewNode;
break;
}
T = T.m_pNode->m_pLeft;
continue;
}
if (v > T.m_pNode->m_nData)
{
if (nullptr == T.m_pNode->m_pRight.m_pNode)
{
NewNode.m_pNode->m_nPosFlag = 1;
NewNode.m_pNode->m_pFatherNode = T;
T.m_pNode->m_pRight = NewNode;
break;
}
T = T.m_pNode->m_pRight;
continue;
}
break;
}
return true;
}
/**
* 删除结点【比较复杂】
*/
virtual bool Delete(N v)
{
// 查找结点
auto T = Find(v);
if (nullptr == T.m_pNode)
{
return false;
}
// 叶子结点
if (nullptr == T.m_pNode->m_pLeft.m_pNode && nullptr == T.m_pNode->m_pRight.m_pNode)
{
//T.DeletePoint();
if (0 == T.m_pNode->m_nPosFlag)
{
T.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == T.m_pNode->m_nPosFlag)
{
T.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
T.DeletePoint();
}
}
// 只有右孩子结点
else if (nullptr == T.m_pNode->m_pLeft.m_pNode)
{
auto temp = T.m_pNode->m_pRight;
T.m_pNode->m_nData = temp.m_pNode->m_nData;
T.m_pNode->m_pLeft = temp.m_pNode->m_pLeft;
T.m_pNode->m_pRight = temp.m_pNode->m_pRight;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
}
// 只有左孩子结点
else if (nullptr == T.m_pNode->m_pRight.m_pNode)
{
auto temp = T.m_pNode->m_pLeft;
T.m_pNode->m_nData = temp.m_pNode->m_nData;
T.m_pNode->m_pLeft = temp.m_pNode->m_pLeft;
T.m_pNode->m_pRight = temp.m_pNode->m_pRight;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
}
// 有双子结点
else
{
auto temp = T.m_pNode->m_pLeft;
// 寻找左孩子最右侧的结点
while (nullptr != temp.m_pNode->m_pRight.m_pNode)
{
temp = temp.m_pNode->m_pRight;
}
T.m_pNode->m_nData = temp.m_pNode->m_nData;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
}
return true;
}
/**
* 判断当前 BST 是否为 AVL 树
* true AVL 树, false 非AVL 树
* 空树不为AVL 树
* 使用了树的后序遍历
*
*/
bool IsAVLTree(KPNode<N>& T)
{
int hl = 0, hr = 0;
if (nullptr != T.m_pNode->m_pLeft.m_pNode)
{
hl = T.m_pNode->m_pLeft.m_pNode->m_nHeight;
}
if (nullptr != T.m_pNode->m_pRight.m_pNode)
{
hr = T.m_pNode->m_pRight.m_pNode->m_nHeight;
}
//判断当前结点为根结点的树是否为AVL 树
if (abs(hl - hr) > 1)
{
return false;
}
T.m_pNode->m_nHeight = max(hl, hr) + 1;
if (nullptr != T.m_pNode->m_pFatherNode.m_pNode)
{
T.m_pNode->m_pFatherNode.m_pNode->m_nHeight++;
T.m_pNode->m_pFatherNode.m_pNode->m_nHeight = max(T.m_pNode->m_pFatherNode.m_pNode->m_nHeight, (T.m_pNode->m_nHeight + 1));
}
return true;
}
virtual bool IsAVLTree()
{
auto T = m_stRoot;
if (nullptr == T.m_pNode)
{
return false;
}
// 保存结点的栈
bool ret = true;
stack<KPNode<N>> node_stack;
node_stack.push(T);
while (!node_stack.empty())
{
auto K = node_stack.top();
node_stack.pop();
if (K.m_pNode->m_nVisit == 2)
{
K.m_pNode->m_nVisit = 0;
ret = IsAVLTree(K);
// 子树不是AVL树的情况
if (!ret)
{
// 记录非AVL树的根结点
m_stpNotAVLNode = T;
return ret;
}
continue;
}
// 当前结点入栈
node_stack.push(K);
// 左结点入栈
if (nullptr != K.m_pNode->m_pRight.m_pNode && 0 == K.m_pNode->m_nVisit)
{
node_stack.push(K.m_pNode->m_pRight);
}
K.m_pNode->m_nVisit++;
// 右结点入栈
if (nullptr != K.m_pNode->m_pLeft.m_pNode && 1 == K.m_pNode->m_nVisit)
{
node_stack.push(K.m_pNode->m_pLeft);
}
K.m_pNode->m_nVisit++;
}
return ret;
}
};
#endif
KAVLTree.h
#ifndef DATA_STRUCT_KTREE_K_A_V_L_TREE_H
#define DATA_STRUCT_KTREE_K_A_V_L_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KBSTree.h"
template<typename N>
/**
* AVL树/平衡二叉排序树
*/
class KAVLTree : public KBSTree<N>
{
protected:
/**
* m_nType:
* L为0 R 为1
* 00 LL 右单旋转
* 11 RR 左单旋转
* 01 LR 先左后右旋转
* 10 RL 先右后左旋转
*/
int m_nType;
//计算 m_nType 所经过的结点路径 -- 包括子树开始的根结点
//vector<KPNode<N>> m_stTypeNodeArray;
int m_nIndex; // 从m_stPassNodeArray数组中,那个下标开始,树开始不平衡了
// 插入/删除 经过的结点数组
vector<KPNode<N>> m_stPassNodeArray;
private:
// 旋转功能里面不做高度的处理
/**
* LL 右单旋转
*/
void LLSpin(KPNode<N> A, KPNode<N> B, KPNode<N> F)
{
// B获得A 的posflag
swap(B.m_pNode->m_nPosFlag, A.m_pNode->m_nPosFlag);
// B 父结点的变化
B.m_pNode->m_pFatherNode = F;
// 左孩子
if (B.m_pNode->m_nPosFlag == 0)
{
F.m_pNode->m_pLeft = B;
}
// 右孩子
else if (B.m_pNode->m_nPosFlag == 1)
{
F.m_pNode->m_pRight = B;
}
// 根结点
else
{
// do nothing;
}
// 根结点的转移
if (2 == B.m_pNode->m_nPosFlag)
{
m_stRoot = B;
}
// B的右子树变为A的左子树
A.m_pNode->m_pLeft = B.m_pNode->m_pRight;
if (nullptr != B.m_pNode->m_pRight.m_pNode)
{
B.m_pNode->m_pRight.m_pNode->m_nPosFlag = 0;
B.m_pNode->m_pRight.m_pNode->m_pFatherNode = A;
}
// A作为B的右结点
B.m_pNode->m_pRight = A;
A.m_pNode->m_nPosFlag = 1;
A.m_pNode->m_pFatherNode = B;
}
/**
* RR 左单旋转
*/
void RRSpin(KPNode<N> A, KPNode<N> B, KPNode<N> F)
{
// B获得A 的posflag
//B.m_pNode->m_nPosFlag = A.m_pNode->m_nPosFlag;
swap(B.m_pNode->m_nPosFlag, A.m_pNode->m_nPosFlag);
// B 父结点的变化
B.m_pNode->m_pFatherNode = F;
// 左孩子
if (B.m_pNode->m_nPosFlag == 0)
{
F.m_pNode->m_pLeft = B;
}
// 右孩子
else if (B.m_pNode->m_nPosFlag == 1)
{
F.m_pNode->m_pRight = B;
}
// 根结点
else
{
// do nothing;
}
// 根结点的转移
if (2 == B.m_pNode->m_nPosFlag)
{
m_stRoot = B;
}
// B的左子树变为A的右子树
A.m_pNode->m_pRight = B.m_pNode->m_pLeft;
if (nullptr != B.m_pNode->m_pLeft.m_pNode)
{
B.m_pNode->m_pLeft.m_pNode->m_nPosFlag = 1;
B.m_pNode->m_pLeft.m_pNode->m_pFatherNode = A;
}
// A作为B的左结点
B.m_pNode->m_pLeft = A;
A.m_pNode->m_nPosFlag = 0;
A.m_pNode->m_pFatherNode = B;
}
/**
* LR 先左后右旋转
*/
void LRSpin(KPNode<N>& A, KPNode<N>& B)
{
RRSpin(B, B.m_pNode->m_pRight, B.m_pNode->m_pFatherNode);
LLSpin(A, A.m_pNode->m_pLeft, A.m_pNode->m_pFatherNode);
}
/**
* RL 先右后左旋转
*/
void RLSpin(KPNode<N>& A, KPNode<N>& B)
{
LLSpin(B, B.m_pNode->m_pLeft, B.m_pNode->m_pFatherNode);
RRSpin(A, A.m_pNode->m_pRight, A.m_pNode->m_pFatherNode);
}
//public:
/**
* 是否为 AVL树
*/
bool IsAVLTree(KPNode<N>& T)
{
int hl = 0, hr = 0;
if (nullptr != T.m_pNode->m_pLeft.m_pNode)
{
hl = T.m_pNode->m_pLeft.m_pNode->m_nHtemp;
}
if (nullptr != T.m_pNode->m_pRight.m_pNode)
{
hr = T.m_pNode->m_pRight.m_pNode->m_nHtemp;
}
//判断当前结点为根结点的树是否为AVL 树
if (abs(hl - hr) > 1)
{
return false;
}
return true;
}
public:
KAVLTree(){}
/**
* 构造函数
*/
KAVLTree(vector<N> v)
{
// 一次插入结点
for (auto n:v)
{
Insert(n);
}
}
/**
* 析构函数
*/
~KAVLTree()
{
}
/**
* 拷贝构造函数
*/
KAVLTree(KAVLTree<N>& rhs) :KBinaryTree(rhs)
{
}
/**
* 赋值函数
*/
KAVLTree<N> operator=(KAVLTree<N>& rhs)
{
KBinaryTree::operator=(rhs);
}
/**
* m_nType:
* L为0 R 为1
* 00 LL 右单旋转
* 11 RR 左单旋转
* 01 LR 先左后右旋转
* 10 RL 先右后左旋转
*/
void AVLSpin()
{
switch (m_nType)
{
case 0: //00 LL 右单旋转
{
m_stPassNodeArray[m_nIndex].m_pNode->m_nHeight -= 1;
for (size_t i = m_nIndex + 1; i < m_stPassNodeArray.size(); i++)
{
m_stPassNodeArray[i].m_pNode->m_nHeight += 1;
}
LLSpin(m_stPassNodeArray[m_nIndex], m_stPassNodeArray[m_nIndex + 1], m_stPassNodeArray[m_nIndex].m_pNode->m_pFatherNode);
}
break;
case 1:// 01 LR 先左后右旋转
{
m_stPassNodeArray[m_nIndex].m_pNode->m_nHeight -= 1;
m_stPassNodeArray[m_nIndex+2].m_pNode->m_nHeight += 2;
for (size_t i = m_nIndex + 3; i < m_stPassNodeArray.size(); i++)
{
m_stPassNodeArray[i].m_pNode->m_nHeight += 1;
}
LRSpin(m_stPassNodeArray[m_nIndex], m_stPassNodeArray[m_nIndex + 1]);
}
break;
case 2:// 10 RL 先右后左旋转
{
m_stPassNodeArray[m_nIndex].m_pNode->m_nHeight -= 1;
m_stPassNodeArray[m_nIndex + 2].m_pNode->m_nHeight += 2;
for (size_t i = m_nIndex + 3; i < m_stPassNodeArray.size(); i++)
{
m_stPassNodeArray[i].m_pNode->m_nHeight += 1;
}
RLSpin(m_stPassNodeArray[m_nIndex], m_stPassNodeArray[m_nIndex + 1]);
}
break;
case 3://11 RR 左单旋转
{
m_stPassNodeArray[m_nIndex].m_pNode->m_nHeight -= 1;
for (size_t i = m_nIndex + 1; i < m_stPassNodeArray.size(); i++)
{
m_stPassNodeArray[i].m_pNode->m_nHeight += 1;
}
RRSpin(m_stPassNodeArray[m_nIndex], m_stPassNodeArray[m_nIndex + 1], m_stPassNodeArray[m_nIndex].m_pNode->m_pFatherNode);
}
break;
default:
break;
}
}
// 设定旋转类型
// 从上向下计算 -- 应对删除操作
void SetAVLSpinType()
{
//m_nType = m_stPassNodeArray[m_nIndex+1].m_pNode->m_nPosFlag << 1;
//m_nType += m_stPassNodeArray[m_nIndex+2].m_pNode->m_nPosFlag
int first = 0; // m_nType的二进制第1位
int second = 0; // m_nType的二进制第0位
auto T = m_stPassNodeArray[m_nIndex];
int hl = 0, hr = 0;
if (nullptr != T.m_pNode->m_pLeft.m_pNode)
{
hl = T.m_pNode->m_pLeft.m_pNode->m_nHtemp;
}
if (nullptr != T.m_pNode->m_pRight.m_pNode)
{
hr = T.m_pNode->m_pRight.m_pNode->m_nHtemp;
}
// m_nType的二进制第1位 求值
if (hl > hr)
{
first = 0;
T = T.m_pNode->m_pLeft;
}
else
{
first = 1;
T = T.m_pNode->m_pRight;
}
if ((int)m_stPassNodeArray.size() > m_nIndex + 1)
{
m_stPassNodeArray[m_nIndex + 1] = T;
}
else
{
m_stPassNodeArray.push_back(T);
}
hl = 0, hr = 0;
if (nullptr != T.m_pNode->m_pLeft.m_pNode)
{
hl = T.m_pNode->m_pLeft.m_pNode->m_nHtemp;
}
if (nullptr != T.m_pNode->m_pRight.m_pNode)
{
hr = T.m_pNode->m_pRight.m_pNode->m_nHtemp;
}
// m_nType的二进制第0位求值
if (hl == hr)
{
second = first;
}
else if (hl > hr)
{
second = 0;
}
else
{
second = 1;
}
///////
if (0 == second)
{
T = T.m_pNode->m_pLeft;
}
else
{
T = T.m_pNode->m_pRight;
}
if ((int)m_stPassNodeArray.size() > m_nIndex + 2)
{
m_stPassNodeArray[m_nIndex + 2] = T;
}
else
{
m_stPassNodeArray.push_back(T);
}
//////
// 计算 m_nType 值
m_nType = first << 1;
m_nType += second;
}
/**
* 插入结点
*/
virtual bool Insert(N v)
{
m_stPassNodeArray.clear();
KPNode<N> NewNode(v);
if (nullptr == m_stRoot.m_pNode)
{
m_stRoot = NewNode;
m_stRoot.m_pNode->m_nPosFlag = 2;
return true;
}
auto IsExsitNode = true;
auto T = m_stRoot;
while (true)
{
m_stPassNodeArray.push_back(T);
if (v < T.m_pNode->m_nData)
{
if (nullptr == T.m_pNode->m_pLeft.m_pNode)
{
NewNode.m_pNode->m_nPosFlag = 0;
NewNode.m_pNode->m_pFatherNode = T;
T.m_pNode->m_pLeft = NewNode;
if (nullptr == T.m_pNode->m_pRight.m_pNode)
{
IsExsitNode = false;
}
break;
}
T = T.m_pNode->m_pLeft;
continue;
}
if (v > T.m_pNode->m_nData)
{
if (nullptr == T.m_pNode->m_pRight.m_pNode)
{
NewNode.m_pNode->m_nPosFlag = 1;
NewNode.m_pNode->m_pFatherNode = T;
T.m_pNode->m_pRight = NewNode;
if (nullptr == T.m_pNode->m_pLeft.m_pNode)
{
IsExsitNode = false;
}
break;
}
T = T.m_pNode->m_pRight;
continue;
}
break;
}
if (IsExsitNode)
{
return true;
}
m_stPassNodeArray.push_back(NewNode);
// 计算 temp 高度
m_stPassNodeArray[m_stPassNodeArray.size() - 1].m_pNode->m_nHtemp = m_stPassNodeArray[m_stPassNodeArray.size() - 1].m_pNode->m_nHeight;
for (int i = (int)m_stPassNodeArray.size()-1; i > 0; i--)
{
m_stPassNodeArray[i - 1].m_pNode->m_nHtemp = max(m_stPassNodeArray[i - 1].m_pNode->m_nHeight, m_stPassNodeArray[i].m_pNode->m_nHtemp + 1);
}
// AVL树的判断及其旋转
for (int i = (int)m_stPassNodeArray.size()-1; i >= 0; i--)
{
bool ret = IsAVLTree(m_stPassNodeArray[i]);
if (!ret)
{
m_nIndex = (int)i;
SetAVLSpinType();
AVLSpin();
break;
}
else
{
m_stPassNodeArray[i].m_pNode->m_nHeight = m_stPassNodeArray[i].m_pNode->m_nHtemp;
}
}
return true;
}
/**
* 删除结点
* 先找到旋转因子,再判断使用什么旋转--找到 导致旋转的差值在哪里
*/
virtual bool Delete(N v)
{
m_stPassNodeArray.clear();
bool ret = true;
auto T = m_stRoot;
auto F = m_stRoot;
while (true)
{
m_stPassNodeArray.push_back(T);
if (nullptr == T.m_pNode)
{
ret = false;
break;
}
if (v < T.m_pNode->m_nData)
{
T = T.m_pNode->m_pLeft;
//m_stPassNodeArray.push_back(T);
continue;
}
if (v > T.m_pNode->m_nData)
{
T = T.m_pNode->m_pRight;
//m_stPassNodeArray.push_back(T);
continue;
}
// 记录被删除结点的父结点
F = T.m_pNode->m_pFatherNode;
break;
}
// 查找值失败
if (!ret)
{
return false;
}
// int nPosFlag = 0; // 结点位置
KPNode<N> stPosNode;
// 叶子结点
if (nullptr == T.m_pNode->m_pLeft.m_pNode && nullptr == T.m_pNode->m_pRight.m_pNode)
{
m_stPassNodeArray.erase(m_stPassNodeArray.begin() + m_stPassNodeArray.size()-1);
//T.DeletePoint();
if (0 == T.m_pNode->m_nPosFlag)
{
stPosNode = T.m_pNode->m_pFatherNode.m_pNode->m_pRight;
T.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == T.m_pNode->m_nPosFlag)
{
stPosNode = T.m_pNode->m_pFatherNode.m_pNode->m_pLeft;
T.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
T.DeletePoint();
m_stRoot.m_pNode = nullptr; // 树变为空树
return true;
}
// 父结点还有子树,高度未变化,仍然是一颗AVL树
if (nullptr != stPosNode.m_pNode && stPosNode.m_pNode->m_nHeight <= 1)
{
return true;
}
}
// 只有右孩子结点
else if (nullptr == T.m_pNode->m_pLeft.m_pNode)
{
auto temp = T.m_pNode->m_pRight;
T.m_pNode->m_nData = temp.m_pNode->m_nData;
T.m_pNode->m_pLeft = temp.m_pNode->m_pLeft;
T.m_pNode->m_pRight = temp.m_pNode->m_pRight;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
}
// 只有左孩子结点
else if (nullptr == T.m_pNode->m_pRight.m_pNode)
{
auto temp = T.m_pNode->m_pLeft;
T.m_pNode->m_nData = temp.m_pNode->m_nData;
T.m_pNode->m_pLeft = temp.m_pNode->m_pLeft;
T.m_pNode->m_pRight = temp.m_pNode->m_pRight;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
}
// 有双子结点
else
{
auto temp = T.m_pNode->m_pLeft;
// 寻找左孩子最右侧的结点
while (nullptr != temp.m_pNode->m_pRight.m_pNode)
{
temp = temp.m_pNode->m_pRight;
}
F = temp.m_pNode->m_pFatherNode;
stPosNode = F.m_pNode->m_pLeft; // 被替换结点的兄弟(左)结点
int data_temp = T.m_pNode->m_nData;
T.m_pNode->m_nData = temp.m_pNode->m_nData;
temp.m_pNode->m_nData = data_temp;
if (0 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pLeft.DeletePoint();
}
else if (1 == temp.m_pNode->m_nPosFlag)
{
temp.m_pNode->m_pFatherNode.m_pNode->m_pRight.DeletePoint();
}
else
{
temp.DeletePoint();
}
// 父结点还有子树,高度未变化,仍然是一颗AVL树
if (nullptr != stPosNode.m_pNode && stPosNode.m_pNode->m_nHeight <= 1)
{
return true;
}
}
// 计算 temp 高度
// 删除跟插入正好相反,要去考虑其兄弟结点对高度的影响
auto brothers = m_stRoot;
if (nullptr != m_stPassNodeArray[m_stPassNodeArray.size() - 1].m_pNode->m_pLeft.m_pNode)
{
brothers = m_stPassNodeArray[m_stPassNodeArray.size() - 1].m_pNode->m_pLeft.m_pNode;
}
else
{
brothers = m_stPassNodeArray[m_stPassNodeArray.size() - 1].m_pNode->m_pRight.m_pNode;
}
if (nullptr != brothers.m_pNode)
{
brothers.m_pNode->m_nHtemp = brothers.m_pNode->m_nHeight;
if (nullptr != brothers.m_pNode->m_pLeft.m_pNode)
{
brothers.m_pNode->m_pLeft.m_pNode->m_nHtemp = brothers.m_pNode->m_pLeft.m_pNode->m_nHeight;
}
else
{
brothers.m_pNode->m_pRight.m_pNode->m_nHtemp = brothers.m_pNode->m_pRight.m_pNode->m_nHeight;
}
}
// 删除后,原父结点不再发生变化
for (int i = (int)m_stPassNodeArray.size() - 1; i > 0; i--)
{
m_stPassNodeArray[i].m_pNode->m_nHtemp = m_stPassNodeArray[i].m_pNode->m_nHeight;
}
// AVL树的判断及其旋转
for (int i = (int)m_stPassNodeArray.size() - 1; i >= 0; i--)
{
bool ret = IsAVLTree(m_stPassNodeArray[i]);
if (!ret)
{
m_nIndex = (int)i;
SetAVLSpinType();
AVLSpin();
break;
}
else
{
m_stPassNodeArray[i].m_pNode->m_nHeight = m_stPassNodeArray[i].m_pNode->m_nHtemp;
}
}
return true;
}
};
#endif
KCBTree.h
#ifndef DATA_STRUCT_KTREE_K_C_B_TREE_H
#define DATA_STRUCT_KTREE_K_C_B_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KBinaryTree.h"
template<typename N>
/**
* complete binary tree 完全二叉树
*/
class KCBTree : public KBinaryTree<N>
{
public:
KCBTree(){}
/**
* 构造函数
*/
KCBTree(vector<N> v)
{
if (v.size() == 0)
{
return;
}
m_stRoot = KPNode<N>(v[0]);
for (size_t i = 1; i < v.size(); i++)
{
LevelTraversal();
for (auto& node : m_hNodeArray)
{
if (nullptr == node.m_pNode->m_pLeft.m_pNode)
{
node.m_pNode->m_pLeft = KPNode<N>(v[i]);
break;
}
if (nullptr == node.m_pNode->m_pRight.m_pNode)
{
node.m_pNode->m_pRight = KPNode<N>(v[i]);
break;
}
}
}
}
/**
* 析构函数
*/
~KCBTree()
{
}
/**
* 拷贝构造函数
*/
KCBTree(KCBTree<N>& rhs):KBinaryTree(rhs)
{
}
/**
* 赋值函数
*/
KCBTree operator=(KCBTree<N>& rhs)
{
if (this == &rhs) return *this;
// 调用基类的 赋值构造函数
KBinaryTree::operator=(rhs);
return *this;
}
};
#endif
KFBTree.h
#ifndef DATA_STRUCT_KTREE_K_F_B_TREE_H
#define DATA_STRUCT_KTREE_K_F_B_TREE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "../KTree/KCBTree.h"
template<typename N>
/**
* full binary tree 满二叉树
* 判断方法 !(i&(i+1)) i是否为 2^n - 1
*/
class KFBTree : public KCBTree<N>
{
protected:
/**
* true 满二叉树构造成功
* false 满二叉树构造失败
*/
bool m_bIsKFBTree;
public:
KFBTree(){}
/**
* 构造函数
*/
KFBTree(vector<N> v) :KCBTree(v)
{
int i = v.size();
m_bIsKFBTree = !(i&(i + 1)) ? true: false;
}
/**
* 析构函数
*/
~KFBTree()
{
}
/**
* 拷贝构造函数
*/
KFBTree(KFBTree<N>& rhs) :KCBTree(rhs)
/**
* 赋值函数
*/
KFBTree operator=(KFBTree<N>& rhs)
{
if (this == &rhs) return *this;
// 调用基类的 赋值构造函数
KCBTree::operator=(rhs);
return *this;
}
/**
* 返回 m_bIsKFBTree成员变量
*/
bool IsSuccess()
{
return m_bIsKFBTree;
}
};
#endif
KHuffmanTree.h
#ifndef DATA_STRUCT_KTREE_K_HUFFMAN_TREE_H
#define DATA_STRUCT_KTREE_K_HUFFMAN_TREE_H
#include <string>
#include <vector>
#include <list>
#include <set>
//#include <multiset>
#include <iostream>
#include <assert.h>
#include "../KTree/KBinaryTree.h"
template<typename N, typename T>
/**
* 哈夫曼树
*/
class KHuffmanTree : public KBinaryTree<N>
{
private:
/**
* 哈夫曼树的最短路径长度
*/
T m_tWPL;
public:
/**
* 构造函数
*/
KHuffmanTree(vector<N> v, vector<T> w)
{
if (v.size() != w.size() || w.size() == 0)
{
return;
}
// 构建结点
//set<KPNode<N>, compare<N>> nodeSet;
multiset<KPNode<N>> nodeSet;
for (size_t i = 0; i < w.size(); i++)
{
KPNode<N> node(v[i]);
node.m_pNode->m_nLeafFlag = 1; // 叶子结点
node.m_pNode->m_nWeight = w[i]; // 叶子结点的权重
m_hNodeArray.push_back(node);
nodeSet.insert(node);
}
// 对结点进行 边排序边构建哈夫曼树
while (nodeSet.size()!= 1)
{
auto first = nodeSet.begin();
(*first).m_pNode->m_nPosFlag = 0;
auto second = first++;
(*second).m_pNode->m_nPosFlag = 1;
KPNode<N> newNode((*first).m_pNode->m_nData + (*second).m_pNode->m_nData);
newNode.m_pNode->m_nWeight = (*first).m_pNode->m_nWeight + (*second).m_pNode->m_nWeight;
newNode.m_pNode->m_pLeft = *first;
newNode.m_pNode->m_pRight = *second;
nodeSet.erase(nodeSet.begin());
nodeSet.erase(nodeSet.begin());
nodeSet.insert(newNode);
}
m_stRoot = *nodeSet.begin();
// 设定路径长度
queue<KPNode<N>> Q;
auto T = m_stRoot;
Q.push(T);
while (!Q.empty())
{
auto K = Q.front();
Q.pop();
if (nullptr != K.m_pNode->m_pRight.m_pNode)
{
K.m_pNode->m_pRight.m_pNode->m_nLength = K.m_pNode->m_nLength + 1;
K.m_pNode->m_pRight.m_pNode->m_strCode = K.m_pNode->m_strCode + "1";
Q.push(K.m_pNode->m_pRight);
}
if (nullptr != K.m_pNode->m_pLeft.m_pNode)
{
K.m_pNode->m_pLeft.m_pNode->m_nLength = K.m_pNode->m_nLength + 1;
K.m_pNode->m_pLeft.m_pNode->m_strCode = K.m_pNode->m_strCode + "0";
Q.push(K.m_pNode->m_pLeft);
}
}
// 计算WPL
m_tWPL = 0;
for (size_t i = 0; i < m_hNodeArray.size(); i++)
{
m_tWPL += m_hNodeArray[i].m_pNode->m_nLength * m_hNodeArray[i].m_pNode->m_nWeight;
}
}
/**
* 析构函数
*/
~KHuffmanTree()
{
}
/**
* 拷贝构造函数
*/
KHuffmanTree(KHuffmanTree<N, T>& rhs) :KBinaryTree(rhs)
{
}
/**
* 赋值函数
*/
KHuffmanTree operator=(KHuffmanTree<N, T>& rhs)
{
if (this == &rhs) return *this;
// 调用基类的 赋值构造函数
KBinaryTree::operator=(rhs);
return *this;
}
/**
* 取得哈夫曼树的最短路径长度
*/
T GetWPL()
{
return m_tWPL;
}
};
#endif
KTreeTest.h
#pragma once //#include "../KTree/KAVLTree.h" #include "../KTree/KAVLTree.h" #include "../KTree/KForest.h" #include "../KTree/KFBTree.h" #include "../KTree/KHuffmanTree.h" void KTreeTest202103151640();
KTreeTest.cpp
#include "KTreeTest.h"
void KTreeTest202103151640()
{
// KTree<int> tree001;
// vector<int> lll;
// 树函数测试
vector<int> data{1,2,3,4,5,6,7,8,9,10};
vector<int> level_num{3,2,1,1,2};
KTree<int> otherTree(data, level_num);
otherTree.PerOrder();
otherTree.PrintNodeArray();
otherTree.PostOrder();
otherTree.PrintNodeArray();
otherTree.LevelTraversal();
otherTree.PrintNodeArray();
vector<int> data1{11, 12, 13, 14, 15, 16, 17, 18, 19, 110};
vector<int> level_num1{3, 2, 1, 1, 2};
KTree<int> otherTree1(data1, level_num1);
otherTree.Union(otherTree1);
otherTree.LevelTraversal();
otherTree.PrintNodeArray();
KPNode<int> node = otherTree1.Select();
cout << "tree select result is " << node.m_pNode->m_nData << endl;
// 树 转 二叉树
// 树函数测试
vector<int> data_03181625{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
vector<int> level_num_03181625{3, 2, 1, 1, 2};
KTree<int> otherTree_03181625(data_03181625,level_num_03181625);
KBinaryTree<int> hKBinaryTree_03181642 = otherTree_03181625.ConvertKBinaryTree();
hKBinaryTree_03181642.LevelTraversal();
hKBinaryTree_03181642.PrintNodeArray();
// 二叉树方法测试
vector<int> data_Binary{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
vector<int> level_num_Binary{2, 1, 1, 2, 2, 0, 1, 0, 0,0};
vector<int> pos_Binary{2,0,1,0,1,0,1,0,1,1};
KBinaryTree<int> hKBinaryTree(data_Binary, level_num_Binary, pos_Binary);
hKBinaryTree.PerOrder();
hKBinaryTree.PrintNodeArray();
hKBinaryTree.PostOrder();
hKBinaryTree.PrintNodeArray();
hKBinaryTree.LevelTraversal();
hKBinaryTree.PrintNodeArray();
KBinaryTree<int> hKBinaryTree_000;
hKBinaryTree_000 = hKBinaryTree;
hKBinaryTree_000.LevelTraversal();
hKBinaryTree_000.PrintNodeArray();
hKBinaryTree_000.MidOrder();
hKBinaryTree_000.PrintNodeArray();
hKBinaryTree.PerOrder();
hKBinaryTree.PrintNodeArray();
hKBinaryTree_000.PreCueing();
//hKBinaryTree_000.ClearCueing();
vector<int> data_Binary_111{1, 2, 3, 4, 5, 6};
vector<int> level_num_Binary_111{1,2,0,2};
vector<int> pos_Binary_111{2,0,0,1,0,1};
KBinaryTree<int> hKBinaryTree_111(data_Binary_111, level_num_Binary_111, pos_Binary_111);
KTree<int> hKBinaryTree_111_tree;
hKBinaryTree_111.LevelTraversal();
hKBinaryTree_111.PrintNodeArray();
bool B61RET = hKBinaryTree_111.ConvertKTree(hKBinaryTree_111_tree);
hKBinaryTree_111_tree.LevelTraversal();
hKBinaryTree_111_tree.PrintNodeArray();
// 二叉树 转 森林
vector<int> data_Binary_03190928{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
vector<int> level_num_Binary_03190928{2, 1, 1, 2, 2, 0, 1, 0, 0, 0};
vector<int> pos_Binary_03190928{2, 0, 1, 0, 1, 0, 1, 0, 1, 1};
KBinaryTree<int> hBinary_03190928(data_Binary_03190928, level_num_Binary_03190928, pos_Binary_03190928);
KForest<int> KForest_03190928;
hBinary_03190928.ConvertKForest(KForest_03190928);
KForest_03190928.LevelTraversal();
KForest_03190928.PrintNodeArray();
// 森林方法测试
cout << "森林测试:" << endl;
vector<int> data_03181850{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
vector<int> level_num_03181850{3, 2, 1, 1, 2};
KTree<int> KForest_tree_03181850(data_03181850, level_num_03181850);
KForest_tree_03181850.LevelTraversal();
KForest_tree_03181850.PrintNodeArray();
vector<int> data_03181851{11, 12, 13, 14, 15, 16, 17, 18, 19, 110};
vector<int> level_num_03181851{3, 2, 1, 1, 2};
KTree<int> KForest_tree_03181851(data_03181851, level_num_03181851);
KForest_tree_03181851.LevelTraversal();
KForest_tree_03181851.PrintNodeArray();
vector<KTree<int>> KForest_tree_array_03181852;
KForest_tree_array_03181852.push_back(KForest_tree_03181850);
KForest_tree_array_03181852.push_back(KForest_tree_03181851);
KForest<int> KForest_03181854(KForest_tree_array_03181852);
KForest_03181854.LevelTraversal();
KForest_03181854.PrintNodeArray();
KBinaryTree<int> hKBinaryTree03181911(KForest_03181854.ConvertKBinaryTree());
hKBinaryTree03181911.LevelTraversal();
hKBinaryTree03181911.PrintNodeArray();
// BST 方法测试
vector<int> data_03191720{32,16,64,8,24,48,80};
KBSTree<int> hKBSTree03191720(data_03191720);
hKBSTree03191720.PerOrder();
hKBSTree03191720.PrintNodeArray();
hKBSTree03191720.LevelTraversal();
hKBSTree03191720.PrintNodeArray();
hKBSTree03191720.Insert(60);
hKBSTree03191720.PerOrder();
hKBSTree03191720.PrintNodeArray();
hKBSTree03191720.Delete(64);
hKBSTree03191720.PerOrder();
hKBSTree03191720.PrintNodeArray();
auto v = hKBSTree03191720.Find(48);
cout << v.m_pNode->m_nPosFlag << endl;
KPNode<int> *p_03191905 = new KPNode<int>(5);
KPNode<int> *p_03191906 = nullptr;
KPNode<int>*& pvp_03191905 = p_03191906;
pvp_03191905 = p_03191905;
delete p_03191905;
p_03191905 = nullptr;
cout << "hKBSTree03191720.IsAVLTree:" << endl;
cout << hKBSTree03191720.IsAVLTree() << endl;
cout << "hKBSTree03191720.Delete(48)" << endl;
hKBSTree03191720.Delete(48);
cout << hKBSTree03191720.IsAVLTree() << endl;
cout << endl;
cout << "hKBSTree03191720.Delete(80)" << endl;
hKBSTree03191720.Delete(80);
cout << endl;
cout << hKBSTree03191720.IsAVLTree() << endl;
cout << "hKBSTree03191720.Delete(60)" << endl;
hKBSTree03191720.Delete(60);
cout << endl;
cout << hKBSTree03191720.IsAVLTree() << endl;
cout << "hKBSTree03191720.IsAVLTree: end" << endl;
// AVL 方法测试
cout << "AVL 方法测试:" << endl;
vector<int> data_03221410{32, 16, 64, 8, 24, 48, 80};
KAVLTree<int> hKAVLTree03191720(data_03221410);
hKAVLTree03191720.PerOrder();
hKAVLTree03191720.PrintNodeArray();
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
KBSTree<int>* PKAVLTree03191720 = &hKAVLTree03191720;
cout << "hKAVLTree03191720 IS AVL TREE:";
cout << PKAVLTree03191720->IsAVLTree() << endl;
// RR 平衡旋转
PKAVLTree03191720->Insert(128);
PKAVLTree03191720->Insert(256);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
// LL 平衡旋转
PKAVLTree03191720->Insert(4);
PKAVLTree03191720->Insert(2);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
// LR 平衡旋转
cout << "LR 平衡旋转:" << endl;
PKAVLTree03191720->Insert(6);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
cout << "hKAVLTree03191720 IS AVL TREE:";
cout << PKAVLTree03191720->IsAVLTree() << endl;
// RL 平衡旋转
cout << "RL 平衡旋转:" << endl;
PKAVLTree03191720->Insert(50);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
PKAVLTree03191720->Insert(49);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
cout << "hKAVLTree03191720 IS AVL TREE:";
cout << PKAVLTree03191720->IsAVLTree() << endl;
// 删除操作
cout << "RR 平衡旋转:" << endl;
PKAVLTree03191720->Delete(49);
PKAVLTree03191720->Delete(50);
PKAVLTree03191720->Delete(48);
hKAVLTree03191720.LevelTraversal();
hKAVLTree03191720.PrintNodeArray();
cout << "hKAVLTree03191720 IS AVL TREE:";
cout << PKAVLTree03191720->IsAVLTree() << endl;
// 完全二叉树方法测试
cout << "完全二叉树方法测试:" << endl;
vector<int> data_03231040{32, 16, 64, 8, 24, 48, 80};
KCBTree<int> hKCBTree_03231040(data_03231040);
hKCBTree_03231040.LevelTraversal();
hKCBTree_03231040.PrintNodeArray();
// 满二叉树方法测试
cout << "满二叉树方法测试:" << endl;
vector<int> data_03231042{32, 16, 64, 8, 24, 48, 80};
KFBTree<int> hKFBTree_03231042(data_03231042);
hKFBTree_03231042.LevelTraversal();
hKFBTree_03231042.PrintNodeArray();
cout << "是否为满二叉树:" << hKFBTree_03231042.IsSuccess() << endl;
vector<int> data_03231043{1,2,3,4,5,6,7,8,9,10,11,12,13,14};
KFBTree<int> hKFBTree_03231043(data_03231043);
hKFBTree_03231043.LevelTraversal();
hKFBTree_03231043.PrintNodeArray();
cout << "是否为满二叉树:" << hKFBTree_03231043.IsSuccess() << endl;
// 哈夫曼树方法测试
cout << "哈夫曼树方法测试:" << endl;
vector<int> data_03231522 {1,2,3,4,5,6};
vector<int> weight_03231522{3,2,1,2,2,1};
KHuffmanTree<int,int> hKHuffmanTree_03231522(data_03231522, weight_03231522);
hKHuffmanTree_03231522.LevelTraversal();
hKHuffmanTree_03231522.PrintNodeArray();
cout << "哈夫曼树 WPL:" << hKHuffmanTree_03231522.GetWPL() << endl;
int i = 0;
i++;
}
结束



 浙公网安备 33010602011771号
浙公网安备 33010602011771号