数据结构 第五章 树-普通树 森林 二叉树

【普通树 森林  二叉树】

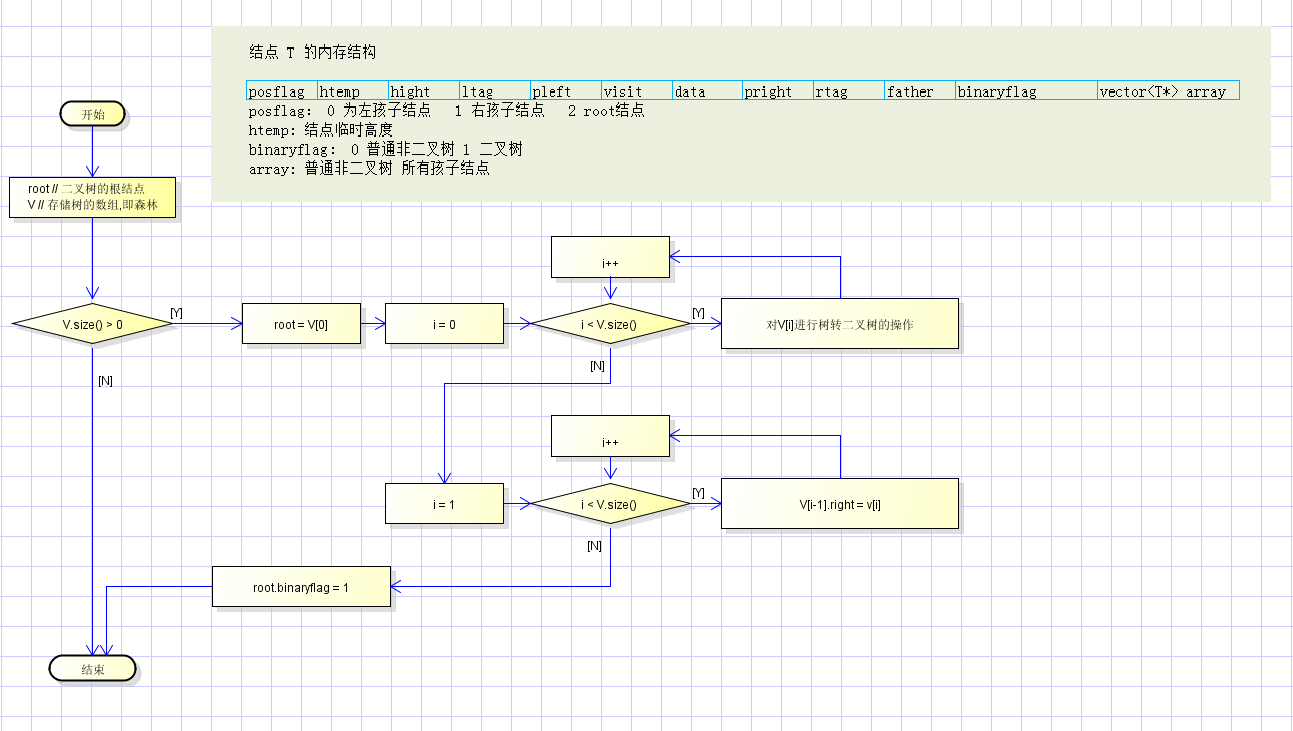
树的存储结点的结构体：

 

 

 * 树的存储结构：双亲表示法、孩子表示法、孩子兄弟表示法{左孩子右兄弟表示法}。

 *双亲表示法：

 

 

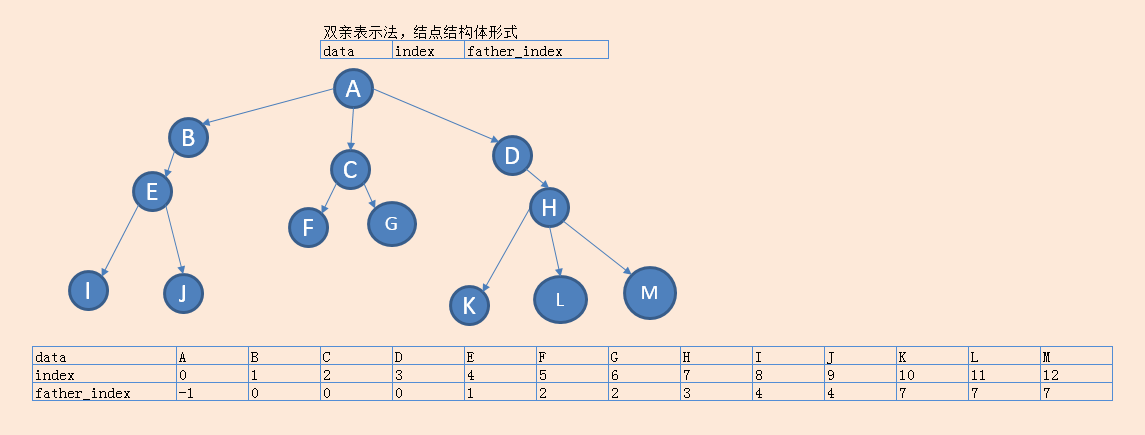
优点：寻找双亲效率高

缺点：寻找孩子效率低

* 孩子表示法

 

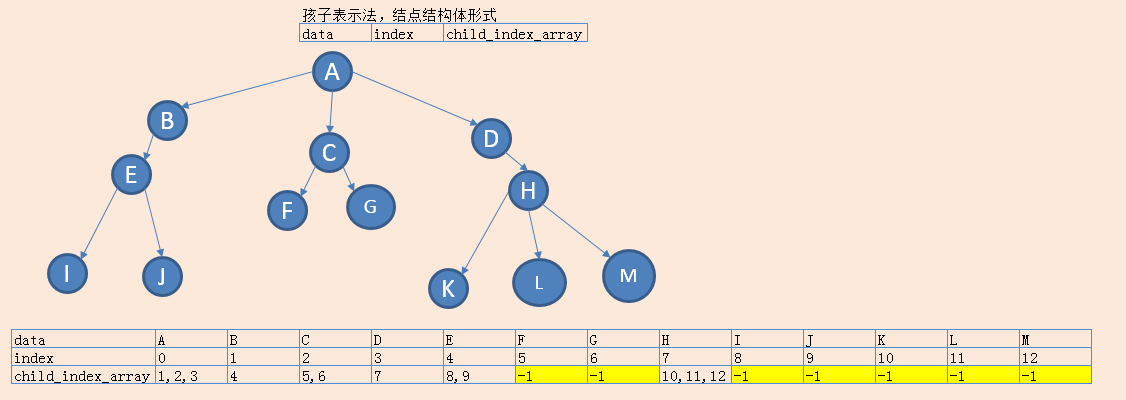
优点：寻找孩子结点效率高

缺点： 寻找双亲结点，效率低

 

* 孩子兄弟表示法{左孩子右兄弟表示法}：

孩子兄弟表示法，采用的是链式存储结构，其存储树的实现思想是：从树的根节点开始，依次用链表存储各个节点的孩子节点和兄弟节点。

  

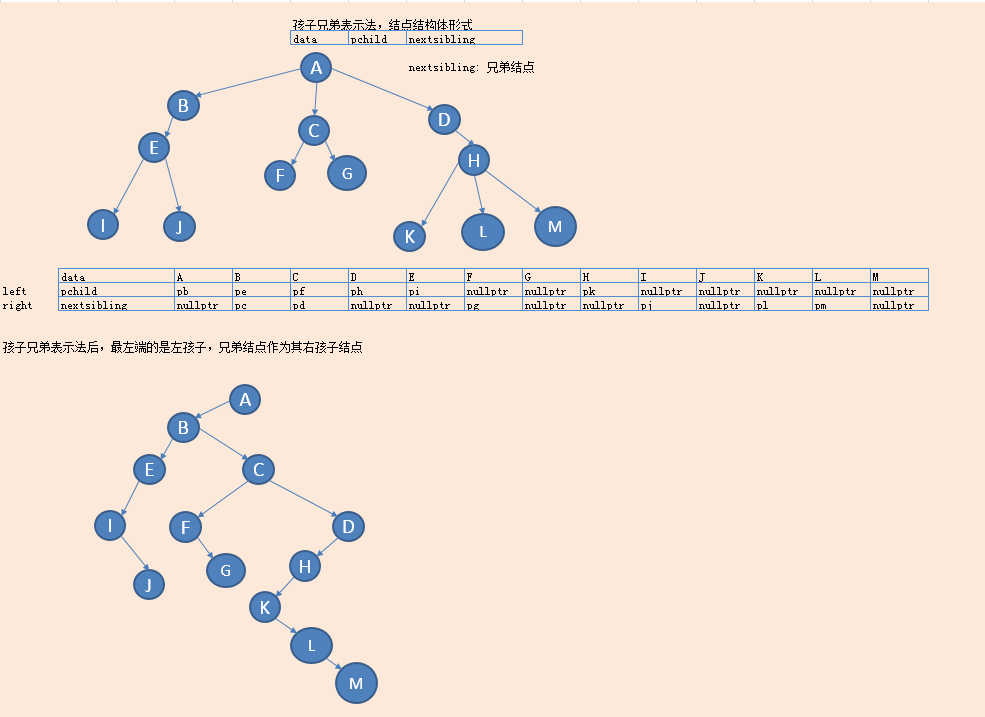
 优点：寻找孩子结点效率高，存储形式类似二叉树，pleft = pchild  pright = nextsibling, 树就变成了一颗二叉树，或者直接使用孩子结点 兄弟结点，不需要做转换。

 缺点：寻找双亲结点的效率低。

* 树与二叉树的转换：

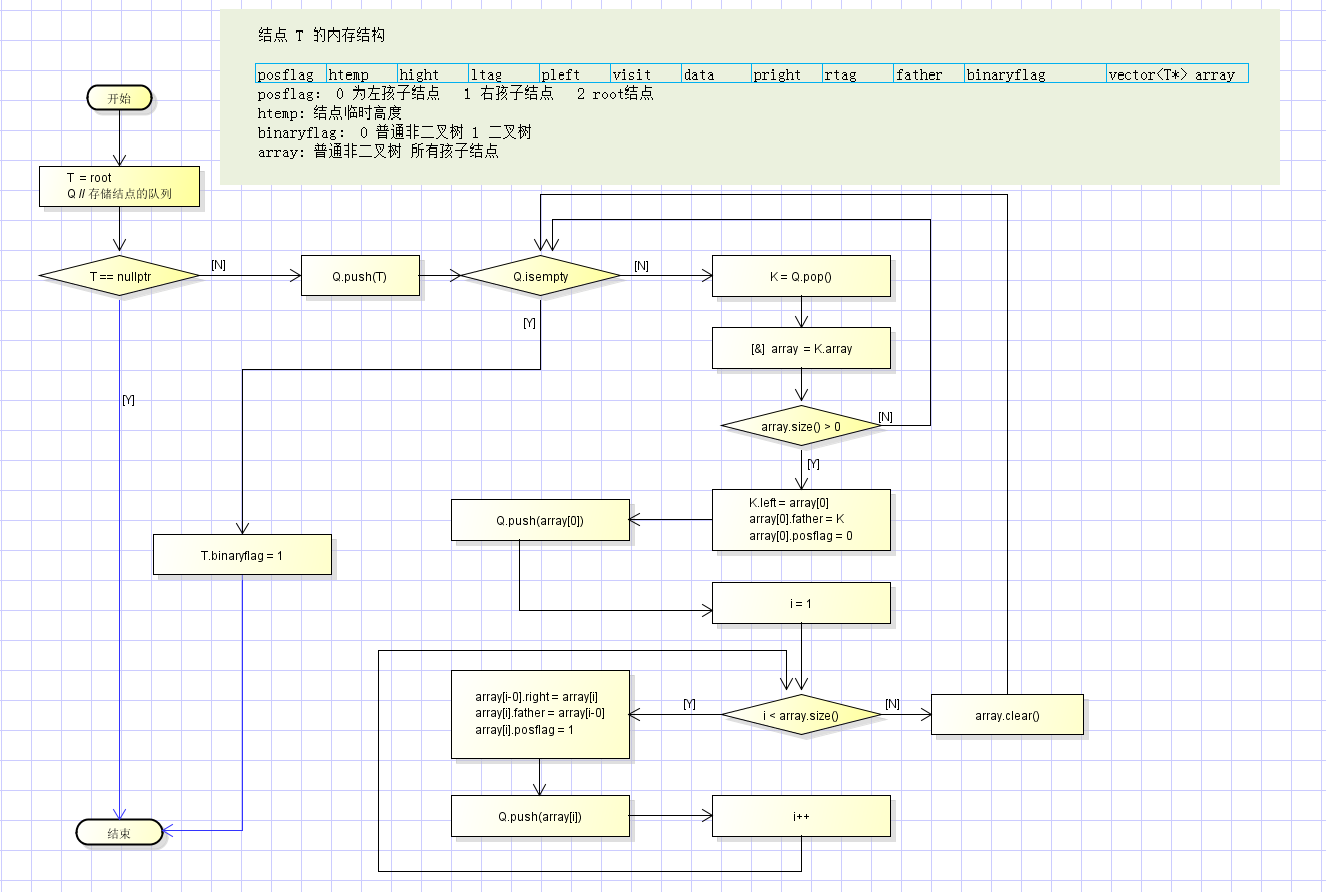
方法1，将树进行层次遍历，结点保存到 vector中，逆序遍历 vector, 使用左孩子有兄弟方式处理结点中的子节点。

方法2，将树进行层次遍历，同一父结点F 的结点集合 V 加连接线，V[i].right = V[i+1];  F.left = V[0];

采用方法2。

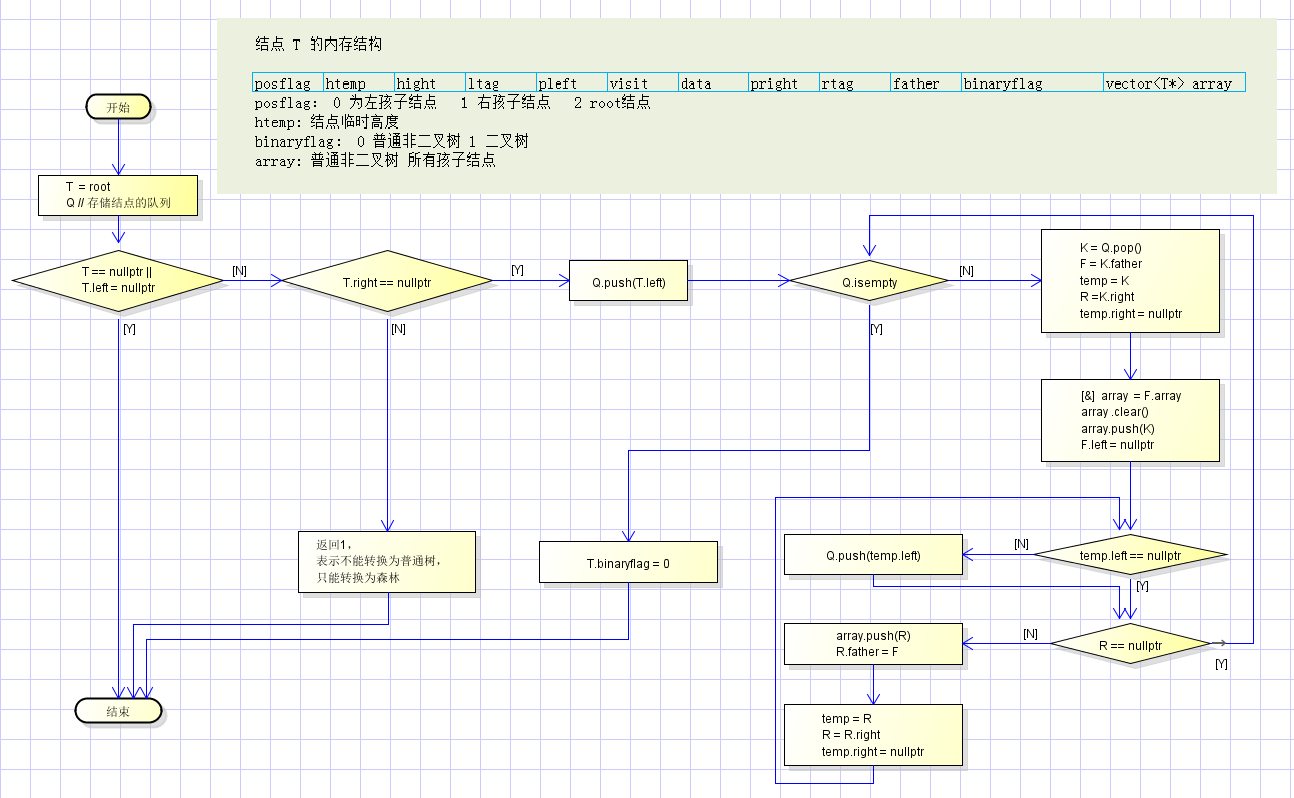
树转二叉树流程图：

 

  

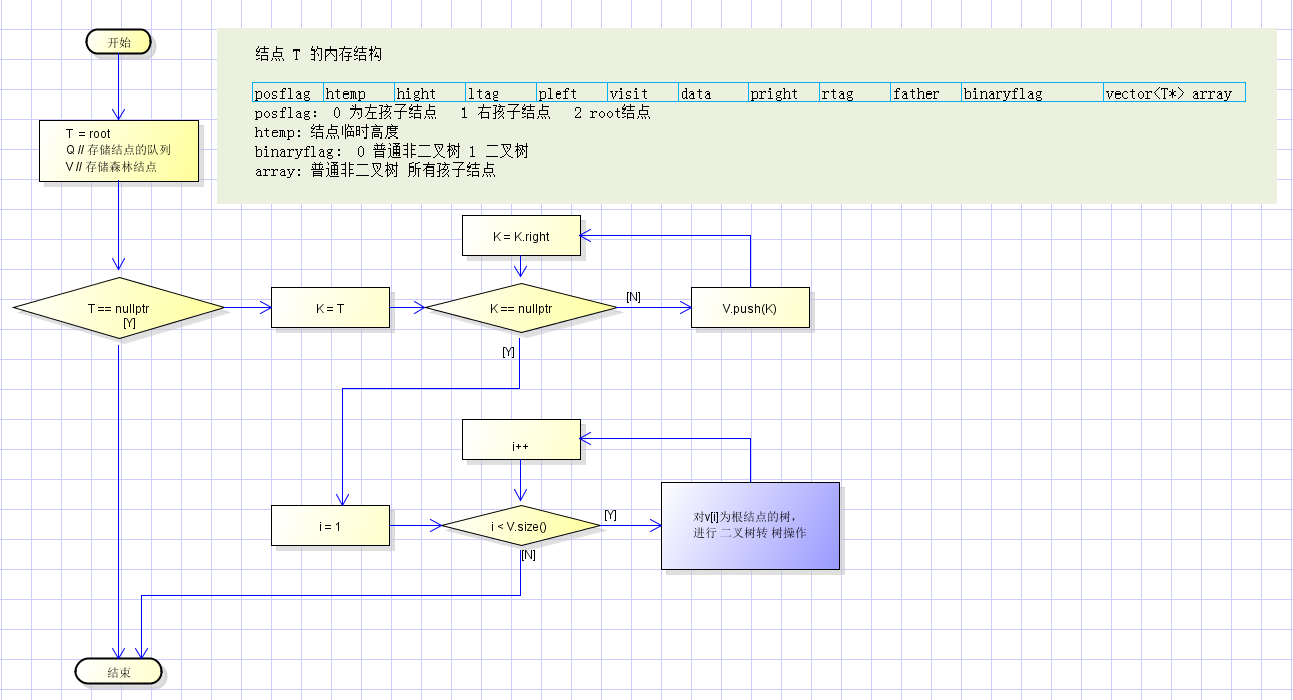
二叉树转树流程图：

 若，根结点的存在右子树，则该二叉树不能转换为普通树 ，可转换为森林。同理，根结点不存在右子树，则该二叉树不能转换为 森林，只能转换为普通树。

 

 

 

 

*森林与二叉树

多棵树构成了森林。 

森林转二叉树。先将每棵树转换为孩子兄弟表示法的二叉树，后面的树依次作为前面的树的右子树。

              

 

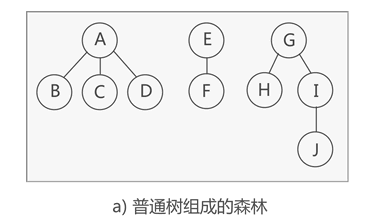
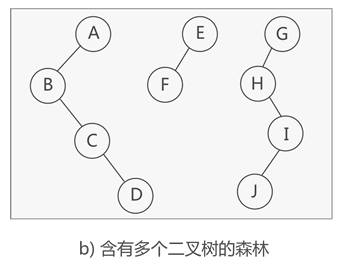
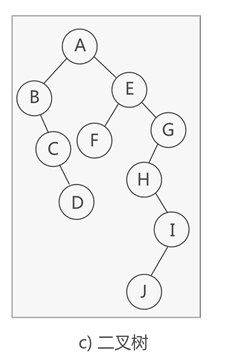
假如一棵二叉树的根节点有右孩子，则这棵二叉树能够转换为森林，否则将转换为一棵树。

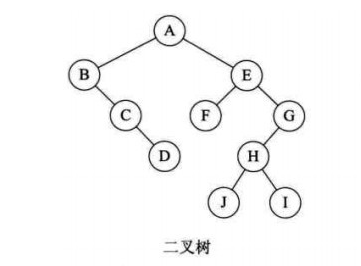
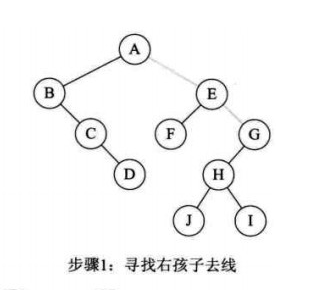
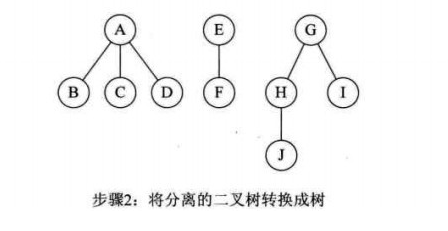
（1）从根节点开始，若右孩子存在，则把与右孩子结点的连线删除。再查看分离后的二叉树，若其根节点的右孩子存在，则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。

（2）将每棵分离后的二叉树转换为树。

 转换步骤如下：

     

 

 

森林转二叉树流程图：

 

 

二叉树转森林流程图：

 

 

 

* 普通树的遍历： 

因为普通树有多个子节点，遍历时，父结点什么时候居中，无法判断，所以不存在树的中序遍历\中根遍历。

剩余三种： 先序、后序、层次 与二叉树的处理逻辑类似，这里赘述。去参照二叉树的逻辑。

 

* 森林的遍历：

森林的遍历，是森林中，从第一棵树，依次按照树 的遍历来的。

如果森林全部是由二叉树构成，则该林存在中序遍历，否则不存在。

其遍历逻辑参照二叉树。

结论：
树的先根遍历序列与这棵树对应二叉树的 先序遍历序列 相同。

树的后根遍历序列与这棵树对应二叉树的 中序遍历序列 相同。

森林的先序遍历序列与该森林对应二叉树的 先序遍历序列 相同。

森林的后根遍历序列与该森林对应二叉树的 中序遍历 序列 相同。

网上好多教程将森林的后根遍历称为中序遍历。不懂。。。。