20162327WJH实验四——图的实现与应用
20162327WJH实验四——图的实现与应用
实 验 报 告
课程:程序设计与数据结构
班级: 1623
姓名: 王旌含
学号:20162327
成绩:
指导教师:娄嘉鹏 王志强
实验日期:11月20日
实验密级: 非密级
预习程度: 已预习
实验时间:15:25-17:15
必修/选修: 必修
实验序号: cs_23
实验内容
实验一
1、实验内容
- 用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
2、实验过程
- 1、顶点的添加及删除方法
public boolean insertVertice(Object obj)
{
return vertices.add(obj);
}
public boolean removeVertice(Object obj){
return vertices.remove(obj);
}
- 2、边的添加及删除方法
public boolean insertEdges(int v1,int v2,int weight) throws Exception
{
boolean result = false;
if((v1 < 0 || v1 >= vertices.size())||(v2 < 0||v2 >= vertices.size()))
{
throw new Exception("v1或者v2参数越界错误!");
}
this.edges[v1][v2]=weight;
this.NumEdges++;
result = true;
return result;
}
//删除某条边
public void removeEdges(int v1,int v2) throws Exception
{
if((v1 < 0 || v1 >= vertices.size())||(v2 < 0||v2 >= vertices.size()))
{
throw new Exception("v1或者v2参数越界错误!");
}
if( v1==v2 || this.edges[v1][v2]==-1)//自己到自己的边或者边不存在则不用删除。
{
throw new Exception("边不存在!");
}
this.edges[v1][v2]=-1;
this.NumEdges--;
}
- 3、遍历的方法
public ArrayList iteratorBFS(int start) throws Exception {
int currentVertex;
int next = -1;
LinkedQueue<Integer> traversalQueue = new LinkedQueue<Integer>();
ArrayList iter = new ArrayList<>();
boolean[] visited = new boolean[vertices.size()];
for (int i = 0; i < visited.length; i++)
visited[i] = false;
traversalQueue.enqueue(start);
visited[start] = true;
while (!traversalQueue.isEmpty()) {
currentVertex = traversalQueue.dequeue();
iter.add(vertices.get(currentVertex));
for (int j = 0; j < visited.length; j++) {
if (edges[currentVertex][j]!=0&&edges[currentVertex][j]!=-1 && !visited[j]) {
traversalQueue.enqueue(j);
visited[j] = true;
}
}
}
return iter;
}
- 4、isEmpty()方法
public boolean isEmpty(Linjie g){
return (vertices.size()==0);
}
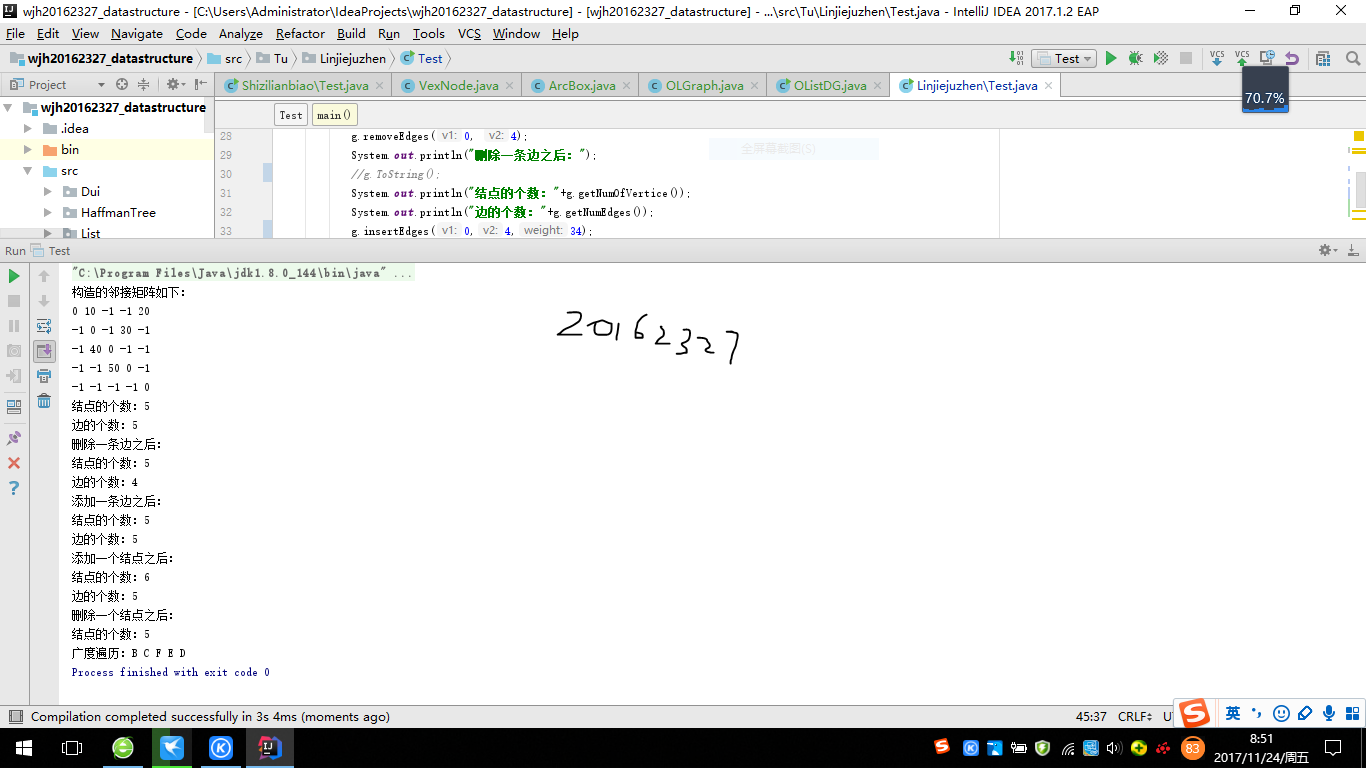
测试截图
实验二
1、实验内容
- 用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
2、实验过程
- 1、构造十字链表过程
public Shizilianbiao(char[] vertex, char[][] edges) {
Numevertex = vertex.length;
Numedges = edges.length;
// 初始化顶点,建立顶点表
vertexNodeList = new VertexNode[Numevertex];
for (int i = 0; i < Numevertex; i++) {
vertexNodeList[i] = new VertexNode();
vertexNodeList[i].vertex = vertex[i];
vertexNodeList[i].firstIn = null;
vertexNodeList[i].firstOut = null;
}
// 初始化边,利用头插法建立十字链表
for (int i = 0; i < Numedges; i++) {
EdgeNode edgeNode1 = new EdgeNode();
EdgeNode edgeNode2 = new EdgeNode();
int vi = getPosition(edges[i][0], vertex);
int vj = getPosition(edges[i][1], vertex);
edgeNode1.endvertex = vi;
edgeNode1.firstvextex = vj;
edgeNode1.endlink = vertexNodeList[vi].firstOut;
vertexNodeList[vi].firstOut = edgeNode1;
edgeNode2.endvertex = vi;
edgeNode2.firstvextex = vj;
edgeNode2.firstlink = vertexNodeList[vj].firstIn;
vertexNodeList[vj].firstIn = edgeNode2;
}
}
- 2、打印邻接表和逆邻接表
public void print() {
System.out.printf("领接表:\n");
for (int i = 0; i < Numevertex; i++) {
System.out.print(vertexNodeList[i].vertex + " ");
if (vertexNodeList[i].firstOut != null) {
EdgeNode EdgeNode2 = new EdgeNode();
EdgeNode2 = vertexNodeList[i].firstOut;
System.out.print(EdgeNode2.firstvextex);
while (EdgeNode2.endlink != null) {
EdgeNode2 = EdgeNode2.endlink;
System.out.print(EdgeNode2.firstvextex);
}
System.out.print("\n");
} else {
System.out.print("\n");
}
}
System.out.print("----------\n");
System.out.printf("逆领接表:\n");
for (int i = 0; i < Numevertex; i++) {
System.out.print(vertexNodeList[i].vertex + " ");
if (vertexNodeList[i].firstIn != null) {
EdgeNode EdgeNode1 = new EdgeNode();
EdgeNode1 = vertexNodeList[i].firstIn;
System.out.print(EdgeNode1.endvertex);
while (EdgeNode1.firstlink != null) {
EdgeNode1 = EdgeNode1.firstlink;
System.out.print(EdgeNode1.endvertex);
}
System.out.print("\n");
} else {
System.out.print("\n");
}
}
}
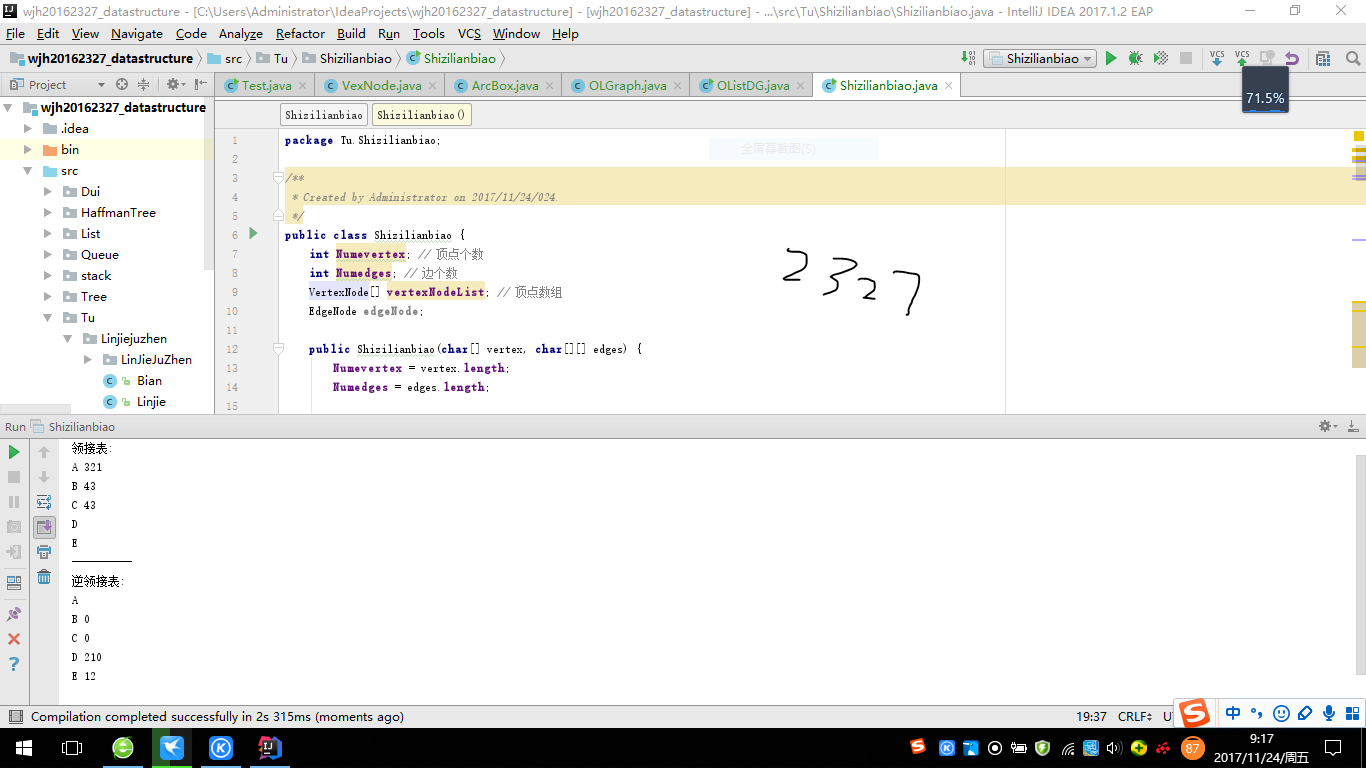
测试截图
实验三
1、实验内容
- 实现PP19.9(实现路由器原理即寻找最短路径问题)
2、实验过程
public class ShortestPath {
// 求取最短路径
public static String[][] getShortestPath(int data[][]) {
int length = data.length;
String path[][] = new String[length][length];
for (int i = 0; i < data.length; i++)
for (int j = 0; j < data[i].length; j++) {
if (data[i][j] > 0)
path[i][j] = (i + 1) + "-->" + (j + 1);
else
path[i][j] = "不通";
}
int k = 0;
while (k < length) {// 循环将各行加入,即计算将k作为最大通过节点之后的最短路径
for (int i = 0; i < length; i++) {
if (data[k][i] > 0) {// 如果这个节点连通了其他节点,则察看是否将影响到当前的最短路径
for (int m = 0; m < length; m++) {
int temp[] = data[m];
if (temp[k] > 0) {// 如果加入当前节点和加入的节点之间是相通的,执行下面的
if (temp[i] < 0) {
if (i != m) {
temp[i] = temp[k] + data[k][i];
path[m][i] = (m + 1) + "-->" + (k + 1)
+ "-->" + (i + 1);
}
} else {
temp[i] = Math.min(temp[k] + data[k][i],
temp[i]);
path[m][i] = path[m][k] + "-->"
+ (i + 1);
}
}
data[m] = temp;
}
}
}
k++;
}
return path;
}
测试截图
- 测试代码
public static void main(String[] args) {
int data[][] = { { -1, 1, 2, -1, -1, -1 }, { -1, -1, 1, 3, -1, 7 },
{ -1, -1, -1, 1, 2, -1 }, { -1, -1, -1, -1, -1, 3 },
{ -1, -1, -1, -1, -1, 6 }, { -1, -1, -1, -1, -1, -1 } };
String pathShow[][] = getShortestPath(data);
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data[i].length; j++) {
if (data[i][j] > 0) {
System.out.print("节点" + (i + 1) + "到节点" + (j + 1)
+ "的最短路径是:" + data[i][j]);
System.out.println(" 路径是" + pathShow[i][j]);
}
}
}
System.out.println("其余没列出的节点之间是不通的");
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号