typedef struct acrnode { int adjvex; struct acrnode *nextarc; }arcnode; typedef struct vnode { acrnode *fristarc; int count;//记入入度的值 }vnode; typedef struct Garph { vnode adlist[maxSize]; int n,e; }Garph; int topsort(Garph g) { int stract[maxSize]; int top=-1; int flag=0; for(int i=0;i<g.n;i++) { if(g.adlist[i].count==0) stract[++top]=i; } while(top!=-1) { int temp=stract[top--]; flag++; acrnode *p; p=g.adlist[temp].fristarc; while(p!=NULL) { int vex=p->adjvex; g.adlist[vex].count--; if(g.adlist[vex].count==0) stract[++top]=vex; p=p->nextarc; } } if(flag==g.n) return 1; else return 0; }
在一个有向图中,对所有的节点进行排序,要求没有一个节点指向它前面的节点。
先统计所有节点的入度,对于入度为0的节点就可以分离出来,然后把这个节点指向的节点的入度减一。
一直做改操作,直到所有的节点都被分离出来。
如果最后不存在入度为0的节点,那就说明有环,不存在拓扑排序,也就是很多题目的无解的情况。
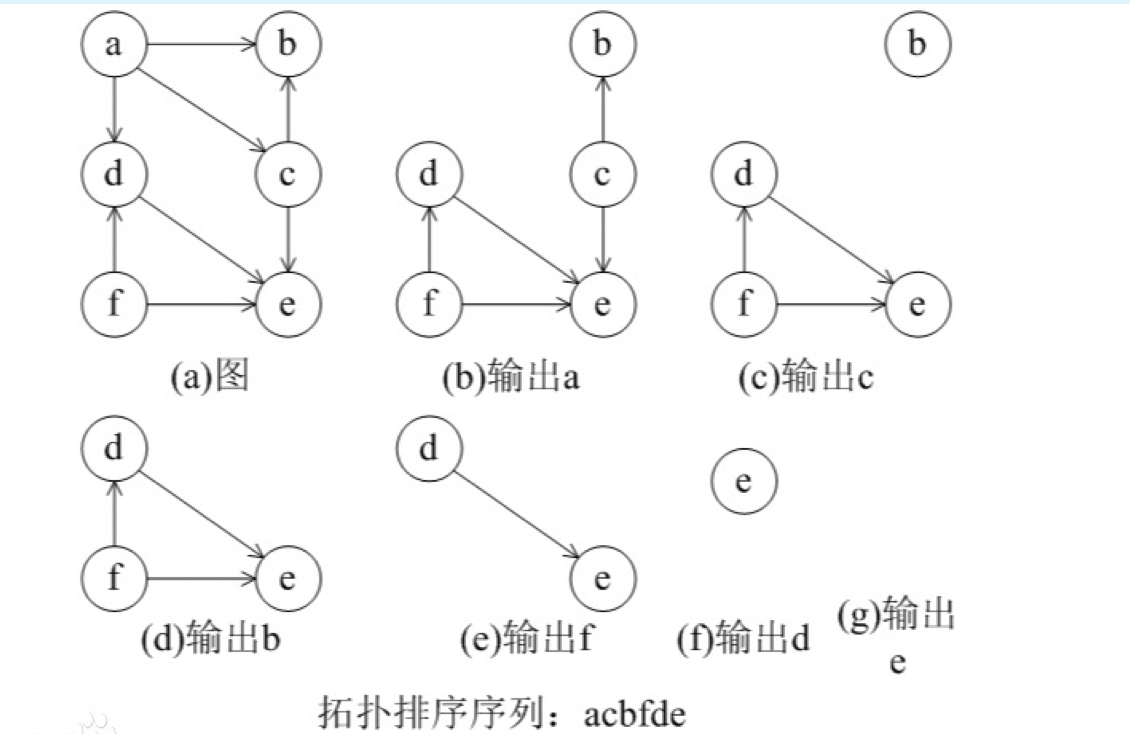
下面是算法的演示过程。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号