算法初识,设计模式,数据结构
我们的算法主要就是在时间上在较劲,我们要通过算法让我们的代码执行效率更高,能够节省更多的时间,我们在实际应用中的场景就是需要尽可能的快,让我们的用户在访问的时候,能够更加流畅的刷新页面能够有更好的用户体验,所以我们需要利用算法来升级我们的代码,所以我们的算法里面有一个时间复杂度的概念,当然了还有空间复杂度,它主要讨论的是内存的问题,这个在实际应用中还是比较好解决的,所以我们主要是讨论时间复杂度,看看哪种算法在应用中更快,更好
递归前菜:

1 def func(x): 2 if x > 0: 3 print("抱着", end='') 4 func(x-1) 5 print("的我", end='') 6 else: 7 print("我的小鲤鱼", end='')
1 def func(x): 2 if x>0: 3 func(x-1) 4 print(x) 5 6 func(3) # 这里是调用函数,并且传参,我们来分析一下这个代码的执行逻辑 7 """ 8 我们把func(3)执行的时候,函数就变成了 9 def func(3): 10 if 3>0: 11 func(3-1) 到这里我们又调用了该函数,就继续去执行函数体里面的代码 12 13 ======= 14 def func(2): 15 if 2>0: 16 func(2-1) 继续调用自己然后去执行函数体的代码 17 18 ======= 19 def func(1): 20 if 1>0: 21 func(0) 继续调用自己然后执行函数体代码 22 23 ======== 24 def func(0): 25 if 0>0: 到这里判断就不成立了,我们就不继续执行了,然后就跳出了自己调用自己的循环,执行下一步print(x)操作,这个操作要返回给函数的调用者,我们的func(0)调用者就是我们的func(1)所以这个时候的func(1)函数的print(x)就是1, 26 再继续往回倒推,func(1)的调用者是func(2)轮到func(2)的时候,就print(2) 27 接着倒推,func(2)的调用者是func(3),到func(3)print(3) 28 再倒推func(3)调用者是func(4)print(4) 29 再倒推func(4)调用者是func(5)print(5) 30 所以我们最后的执行结果是 31 32 """ 33 34 1 35 2 36 3 37 4 38 5
low_B三人组
冒泡排序:
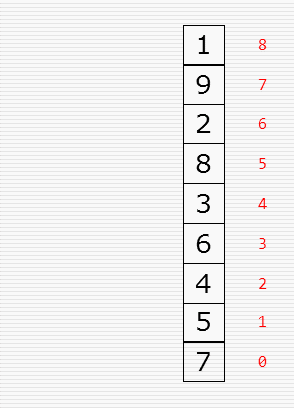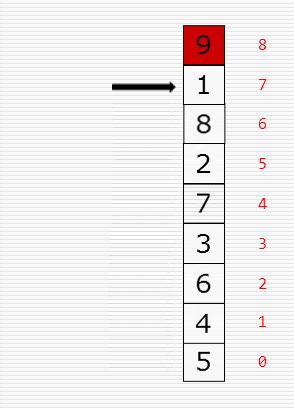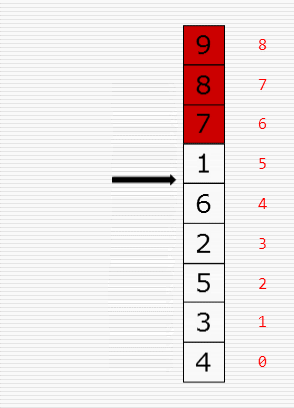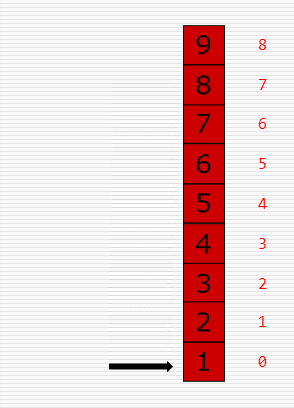
直接插入排序
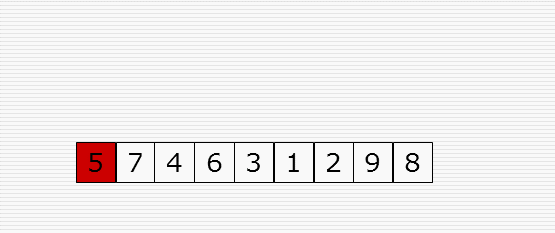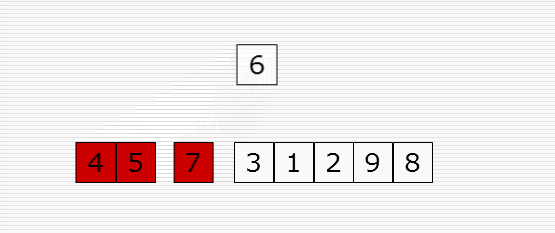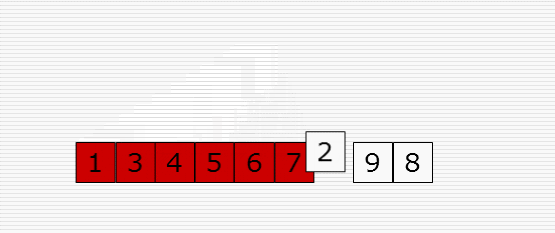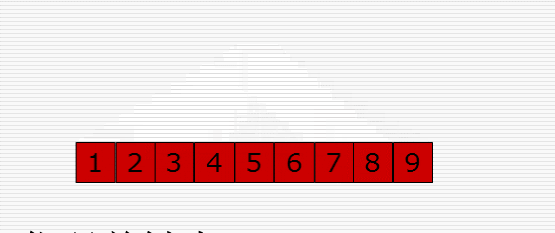

1 import random 2 import time 3 4 def cal_time(func): 5 def inner(*args, **kwargs): 6 time1 = time.time() 7 res = func(*args, **kwargs) 8 time2 = time.time() 9 print("Time: %f" % (time2 - time1)) 10 return res 11 return inner 12 13 @cal_time 14 def bubble_sort(li): 15 # 冒泡排序 16 for i in range(len(li)-1): # i表示第几趟 17 for j in range(len(li)-i-1): # j表示图中的箭头 18 if li[j] > li[j+1]: 19 li[j], li[j+1] = li[j+1], li[j] 20 21 @cal_time 22 def bubble_sort_1(li): 23 # 冒泡排序优化 24 for i in range(len(li)-1): # i表示第几趟 25 exchange = False 26 for j in range(len(li)-i-1): # j表示图中的箭头 27 if li[j] > li[j+1]: 28 li[j], li[j+1] = li[j+1], li[j] 29 exchange = True 30 if not exchange: 31 return 32 33 @cal_time 34 def select_sort(li): 35 # 选择排序 36 for i in range(len(li)-1): 37 # 第i趟开始时 无序区:li[i:] 38 # 找无序区最小值,保存最小值的位置 39 min_pos = i # min_pos保存最小值的位置 40 for j in range(i+1, len(li)): 41 if li[j] < li[min_pos]: 42 min_pos = j 43 li[min_pos], li[i] = li[i], li[min_pos] 44 45 46 @cal_time 47 def insert_sort(li): 48 # 插入排序 49 for i in range(1, len(li)): # i是摸到的牌的下标 50 tmp = li[i] 51 j = i - 1 # j是手里最后一张牌的下标 52 while j >= 0 and li[j] > tmp: # 两个终止条件:j小于0表示tmp是最小的 顺序不要乱 53 li[j+1] = li[j] 54 j -= 1 55 # for j in range(i-1, -1, -1): 56 # if li[j] > tmp: 57 # li[j+1] = li[j] 58 # else: 59 # break 60 li[j+1] = tmp 61 62 63 64 65 66 67 li = list(range(10000)) 68 random.shuffle(li) 69 insert_sort(li) 70 print(li) 71 72 73 # 布尔运算的短路功能
1 t = 0 2 3 def hanoi(n, A, B, C): 4 """ 5 :param n: 问题规模 6 :param A: 起始盘子 7 :param B: 路过盘子 8 :param C: 目标盘子 9 :return: 10 """ 11 if n > 0: 12 hanoi(n-1, A, C, B) 13 14 print("%s->%s" % (A, C)) 15 hanoi(n-1, B, A, C) 16 17 18 hanoi(6, 'A', 'B', 'C') 19 print(t)
牛逼三人组
快速排序
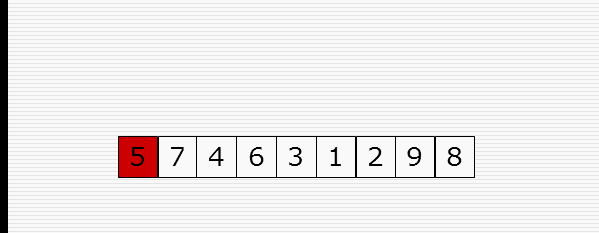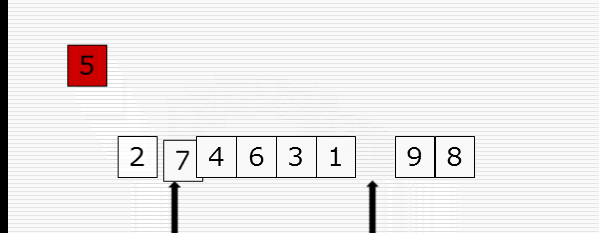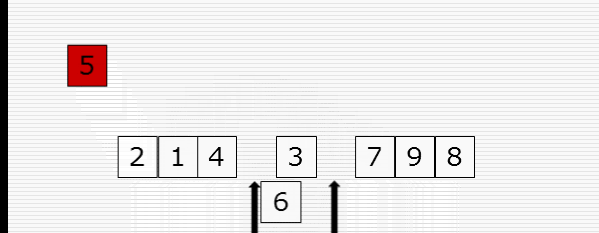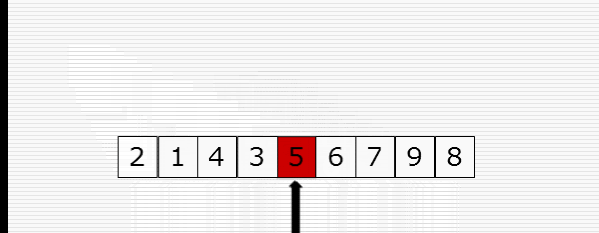

1 import random 2 import time 3 import sys 4 5 sys.setrecursionlimit(100000000) 6 7 def cal_time(func): 8 def inner(*args, **kwargs): 9 time1 = time.time() 10 res = func(*args, **kwargs) 11 time2 = time.time() 12 print("Time: %f" % (time2 - time1)) 13 return res 14 return inner 15 16 def partition(li, left, right): 17 randi = random.randint(left, right) 18 li[randi], li[left] = li[left], li[randi] 19 20 tmp = li[left] 21 while left < right: 22 while left < right and li[right] >= tmp: 23 right -= 1 24 li[left] = li[right] 25 while left < right and li[left] <= tmp: 26 left += 1 27 li[right] = li[left] 28 li[left] = tmp 29 return left 30 31 32 def _quick_sort(li, left, right): 33 if left < right: # 至少两个元素 34 mid = partition(li, left, right) 35 _quick_sort(li, left, mid - 1) 36 _quick_sort(li, mid + 1, right) 37 38 @cal_time 39 def quick_sort(li): 40 return _quick_sort(li, 0, len(li)-1) 41 42 43 li = list(range(10000, 0, -1)) 44 quick_sort(li)
快排详细解析,虽然是用于C语言的,但是,思路跟逻辑是一样的,里面有不同解决思路的推理过程,还是能有很大帮助的。
https://blog.csdn.net/xy913741894/article/details/59110569
堆排序

欧飞龙总结的堆排序代码
具体代码: def sift(li, low, high): # low是子树的根节点的下标值,high是子树最后一个节点的下标值,我们的下标是从最上面开始往下数的,上面是列表的第一个值,依次往后, # i指向堆顶 i = low # j指向堆顶的左孩子 j = 2 * i + 1 while j <= high: # 如果j>high,那么就说明我们的i已经到树底部了,也就是说我们的i已经是最后的叶子节点了,那样就不需要调整了,直接跳出循环. # 判断左孩子和右孩子哪个小, j就指向谁 if j + 1 <= high and li[j + 1] < li[j]: j += 1 # 判断堆顶和孩子哪个小,如果堆顶小,跳出循环,如果孩子小,和堆顶进行交换,然后以孩子当作堆顶,继续判断 if li[j] < li[i]: # 如果叶子节点数值比根节点的数值大,就需要调整位置,我们最后要达到的状态是根节点的值最大,然后依次往下逐渐越来越小. li[i], li[j] = li[j], li[i] i = j j = 2 * i + 1 else: # 如果根节点的值本身就比叶子节点大,那么就不需要做调整了. break def heap_sort(li, k): # 取前k个数建小根堆 for i in range(k // 2 - 1, -1, -1): sift(li, i, k - 1) # 遍历列表的k-len(li)-1,和堆顶做比较 for j in range(k, len(li)): if li[j] > li[0]: # 如果比堆顶大,和堆顶交换 li[0], li[j] = li[j], li[0] # 调整堆,确保堆顶是整个堆的最小值 sift(li, 0, k - 1) # 出堆 for n in range(k - 1, 0, -1): # 让堆顶和堆的最后一个值交换,然后把最后那个值从堆去掉 li[0], li[n] = li[n], li[0] # 调整堆,确保堆顶是堆的最小值 sift(li, 0, n - 1) return li[0:k] li = list(range(1000)) import random random.shuffle(li) res = heap_sort(li, 10) print(res)
sift函数里面的参数,low是子树的根,high是子树的最大的叶子节点,这里的low是指索引最小,high也是指索引值,

1 import random 2 import time 3 import copy 4 5 def cal_time(func): 6 def inner(*args, **kwargs): 7 time1 = time.time() 8 res = func(*args, **kwargs) 9 time2 = time.time() 10 print("Time: %f" % (time2 - time1)) 11 return res 12 return inner 13 14 def sift(li, low, high): 15 tmp = li[low] 16 i = low 17 j = 2 * i + 1 18 while j <= high: # 退出条件2:当前i位置是叶子结点,j位置超过了high 19 # j 只想更大的孩子 20 if j + 1 <= high and li[j+1] > li[j]: 21 j = j + 1 # 如果右孩子存在并且更大,j指向右孩子 22 if tmp < li[j]: 23 li[i] = li[j] 24 i = j 25 j = 2 * i + 1 26 else: # 退出条件1:tmp的值大于两个孩子的值 27 break 28 li[i] = tmp 29 30 @cal_time 31 def heap_sort(li): 32 # 1. 建堆 33 n = len(li) 34 for i in range(n//2-1, -1, -1): 35 # i 是建堆时要调整的子树的根的下标 36 sift(li, i, n-1) 37 # 2.挨个出数 38 for i in range(n-1, -1, -1): #i表示当前的high值 也表示棋子的位置 39 li[i], li[0] = li[0], li[i] 40 # 现在堆的范围 0~i-1 41 sift(li, 0, i-1) 42 43 @cal_time 44 def sys_sort(li): 45 li.sort() 46 47 # li = list(range(1000000)) 48 # random.shuffle(li) 49 # li2 = copy.deepcopy(li) 50 # 51 # heap_sort(li) 52 # sys_sort(li2) 53 54 import heapq 55 56 57 li = list(range(10)) 58 random.shuffle(li) 59 # print(li) 60 # heapq.heapify(li) 61 # print(li) 62 # heapq.heappush(li, 10) 63 # print(li) 64 # print(heapq.heappop(li)) 65 # print(heapq.heappop(li)) 66 # print(heapq.heappop(li)) 67 68 print(heapq.nsmallest(3, li))
组长总结的高阶版:
class Heap: def __init__(self, sign=1): self.heap = [] # 堆列表 self.tail = 0 # 标记堆尾 self.sign = sign # 标记大/小跟堆,1表示大根堆,-1表示小根堆 def _exchange_down(self, index, leaf): """ 判断是否需要交换并下沉。 这是下沉函数的辅助函数,用来被考察:这个节点和他被选出的叶,是否需要交换。 并执行下一步下沉。 :param index: 考察节点 :param leaf: 被比较的节点 """ if (self.heap[index] - self.heap[leaf]) * self.sign < 0: self.heap[index], self.heap[leaf] = self.heap[leaf], self.heap[index] self._shift_down(leaf) # 换下来的值可能不满足堆的条件,所以它需要检验下沉。 def _shift_up(self, index): """ 上浮函数 :param index: 考察是否上浮的页节点 """ father = index//2 if father > 0: if (self.heap[index]-self.heap[father])*self.sign > 0: self.heap[index], self.heap[father] = self.heap[father], self.heap[index] self._shift_down(index) # 换下来的值可能不满足堆的条件,所以它需要检验下沉。 self._shift_up(father) # 换上去的父节点可能依然不满足堆条件,所以让他继续上浮。 def _shift_down(self, index): """ 下沉函数: :param index: 考察是否上浮的页节点 """ leaf_l = index*2 leaf_r = leaf_l+1 if leaf_l > self.tail: # 没有页节点 return elif leaf_r > self.tail: # 只有左叶节点 self._exchange_down(index, leaf_l) else: # 有两个页节点 if (self.heap[leaf_l] - self.heap[leaf_r])*self.sign > 0: self._exchange_down(index, leaf_l) else: self._exchange_down(index, leaf_r) def sort(self, aim): """ 堆排序函数。 更优雅:以索引1位置为整个堆的根节点。(牺牲一定的效率,可优化为以0为根) 这样的话。对于任意的节点,他的父节点都它索引整除2的节点。 它的叶就是2n和2n+1。 :param aim: 需要排序的列表。 """ # 将第0个元素放在末尾。(len(aim)+1,可优化。) aim.append(aim[0]) self.tail = len(aim)-1 self.heap = aim # 构建堆,自堆底依次上浮。 for i in range(len(aim)-1, 0, -1): self._shift_up(i) # 交换末尾节点和堆顶,再下沉堆被换上来的堆顶元素。 for i in range(len(aim)-1): self.heap[1], self.heap[self.tail] = self.heap[self.tail], self.heap[1] self.tail -= 1 self._shift_down(1) aim.pop(0) # 最后把多余的第0个元素删除。
归并排序


1 import random 2 3 def merge(li, low, mid, high): 4 """ 5 low~mid有序, mid+1~high有序 6 :param li: 7 :param low: 8 :param mid: 9 :param high: 10 :return: 11 """ 12 i = low 13 j = mid + 1 14 ltmp = [] 15 while i <= mid and j <= high: 16 if li[i] < li[j]: 17 ltmp.append(li[i]) 18 i += 1 19 else: 20 ltmp.append(li[j]) 21 j += 1 22 while i <= mid: 23 ltmp.append(li[i]) 24 i += 1 25 while j <= high: 26 ltmp.append(li[j]) 27 j += 1 28 # for k in range(low, high+1): 29 # li[k] = ltmp[k-low] 30 li[low:high+1] = ltmp 31 32 def merge_sort(li, low, high): 33 if low < high: 34 mid = (low + high) // 2 35 merge_sort(li, low, mid) 36 merge_sort(li, mid+1, high) 37 merge(li, low, mid, high) 38 39 # li = list(range(10000)) 40 # random.shuffle(li) 41 # merge_sort(li, 0, len(li)-1) 42 # print(li) 43 li = [10,4,6,3,8,2,5,7] 44 merge_sort(li, 0, len(li)-1)
伟大的希尔排序思想
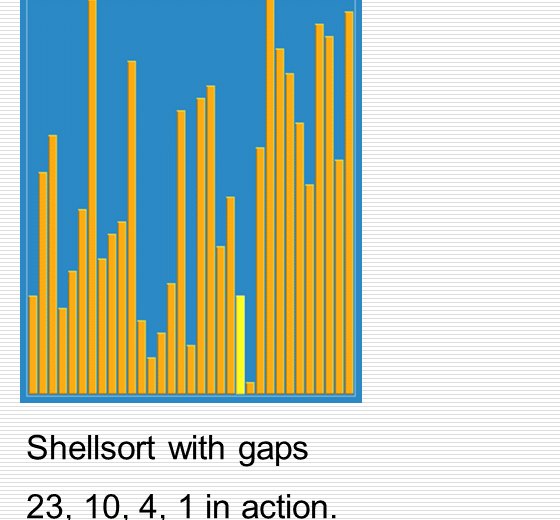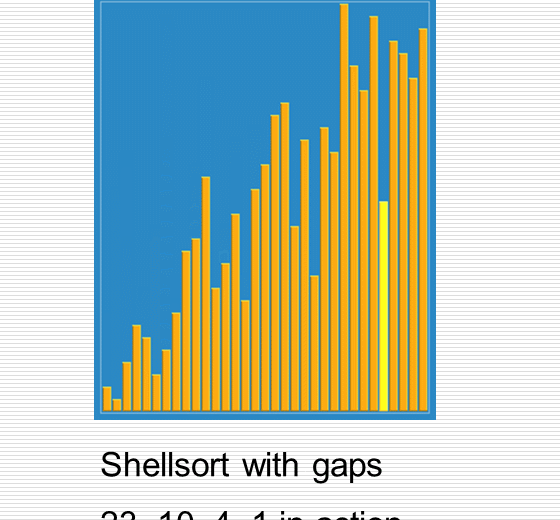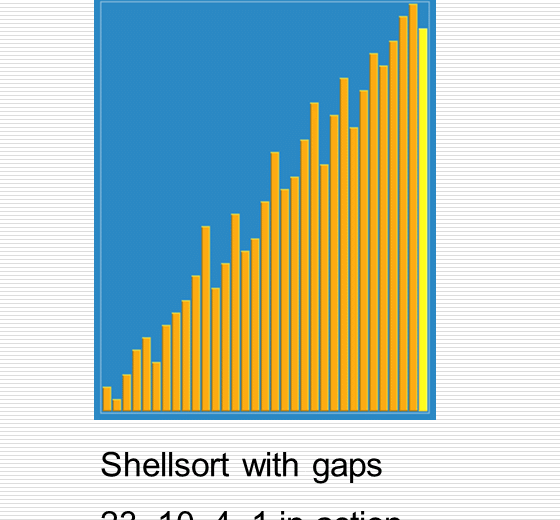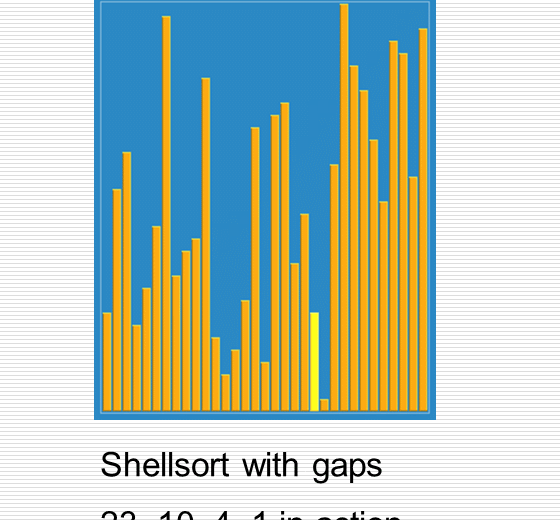


1 import random 2 import time 3 import sys 4 import copy 5 6 sys.setrecursionlimit(100000000) 7 8 def cal_time(func): 9 def inner(*args, **kwargs): 10 time1 = time.time() 11 res = func(*args, **kwargs) 12 time2 = time.time() 13 print("Time: %f" % (time2 - time1)) 14 return res 15 return inner 16 17 def partition(li, left, right): 18 randi = random.randint(left, right) 19 li[randi], li[left] = li[left], li[randi] 20 21 tmp = li[left] 22 while left < right: 23 while left < right and li[right] >= tmp: 24 right -= 1 25 li[left] = li[right] 26 while left < right and li[left] <= tmp: 27 left += 1 28 li[right] = li[left] 29 li[left] = tmp 30 return left 31 32 33 def _quick_sort(li, left, right): 34 if left < right: # 至少两个元素 35 mid = partition(li, left, right) 36 _quick_sort(li, left, mid - 1) 37 _quick_sort(li, mid + 1, right) 38 39 @cal_time 40 def quick_sort(li): 41 return _quick_sort(li, 0, len(li)-1) 42 43 44 def insert_sort_gap(li, gap): 45 for i in range(1, len(li)): # i是摸到的牌的下标 46 tmp = li[i] 47 j = i - gap # j是手里最后一张牌的下标 48 while j >= 0 and li[j] > tmp: # 两个终止条件:j小于0表示tmp是最小的 顺序不要乱 49 li[j+gap] = li[j] 50 j -= gap 51 li[j+gap] = tmp 52 53 @cal_time 54 def shell_sort(li): 55 d = len(li) // 2 56 while d > 0: 57 insert_sort_gap(li, d) 58 d = d // 2 59 60 61 li = list(range(100000)) 62 random.shuffle(li) 63 li2 = copy.deepcopy(li) 64 shell_sort(li) 65 quick_sort(li2)

1 import time 2 3 def cal_time(func): 4 def inner(*args, **kwargs): 5 time1 = time.time() 6 res = func(*args, **kwargs) 7 time2 = time.time() 8 print("Time: %f" % (time2 - time1)) 9 return res 10 return inner 11 12 @cal_time 13 def binary_search(li, val): 14 low = 0 15 high = len(li) - 1 16 while low <= high: 17 mid = (low + high) // 2 18 if li[mid] < val: 19 low = mid + 1 20 elif li[mid] > val: 21 high = mid - 1 22 else: 23 return mid 24 return None 25 26 @cal_time 27 def linear_search(li, val): 28 try: 29 return li.index(val) 30 except: 31 return None 32 33 34 li = list(range(0, 10000000, 2)) 35 binary_search(li, 9548006) 36 linear_search(li, 9548006)
加注释的代码块:
列表查找:

1 li0 = [3, 5, 6, 8, 9, 7, 4, ] 2 3 4 # for i in range(len(li)-1): 5 # print("这里是i",i) # 这里的i是列表的索引值 6 # for j in range(i+1,len(li)): 7 # print("这里是j",j) # 这里的j打印出来的是列表中每一个元素的索引值,所以上面的i+1就是在索引上+1 8 def select_sort(li): 9 for i in range(len(li) - 1): 10 min_loc = i 11 for j in range(i + 1, len(li)): 12 # print(li[j]) 13 print(li[min_loc]) 14 if li[j] < li[min_loc]: 15 # print(li[j]) 16 """ 17 4 18 5 19 7 20 6 21 7 22 8 23 """ 24 # print(li[min_loc]) 25 """ 26 5 27 6 28 8 29 7 30 9 31 9 32 """ 33 min_loc = j 34 if min_loc != i: 35 li[i], li[min_loc] = li[min_loc], li[i] 36 37 38 select_sort(li0) 39 # print(li0)

1 import random 2 import time 3 4 l = [2, 3, 1, 6, 43, 23, 4] 5 6 7 def cal_time(func): 8 """ 9 这里是计算时间的装饰器 10 :param func: 11 :return: 12 """ 13 14 def inner(*args, **kwargs): 15 time1 = time.time() 16 ret = func(*args, **kwargs) 17 time2 = time.time() 18 print('Time:%s' % (time2 - time1)) 19 return ret 20 21 return inner 22 23 24 def bubble_sort(li): 25 # 冒泡排序 26 for i in range(len(li) - 1): # i表示第几趟 27 for j in range(len(li) - i - 1): # j表示图中的箭头 28 if li[j] > li[j + 1]: 29 li[j], li[j + 1] = li[j + 1], li[j] 30 31 # bubble_sort(l) 32 # print(l) 33 34 def bubble_sort_2(li): 35 # 再不理解就想我们PPT里面的动图效果 36 # 冒泡排序优化我们加了一个exchange判断 37 for i in range(len(li) - 1): # i表示第几趟 38 exchange = False # 增加了一个标志位,用于判断顺序是否有序,跳出循环用 39 for j in range(len(li) - i - 1): # j表示图中的箭头,len(li)-i-1是剩余未归位区最大的索引 40 if li[j] > li[j + 1]: # 这里是在无序区里面我们的两个数据进行比较,如果满足条件就进行顺序调换 41 li[j], li[j + 1] = li[j + 1], li[j] 42 exchange = True 43 if not exchange: 44 return 45 46 47 def select_sort(li): 48 # 选择排序 49 for i in range(len(li) - 1): 50 """ 51 第i趟开始时,无序区:li[i:]所有数据都是在无序区里面的 52 """ 53 min_pos = i # 我们把第一次循环得到的值保存到这个变量里面来 54 for j in range(i + 1, len(li)): # 因为自己不能跟自己比较,所以我们需要从i+1开始循环 55 if li[j] > li[min_pos]: # 这里我们的j就是我们第二次循环里面的数据,它是排除了我们第一次循环取到的值的剩余的数据, 56 # 这里就是我们第一次循环的值跟后面第二次循环的值进行比较,如果满足条件那么就调换位置,按照从小到大的顺序来, 57 # 如果要从大到小就把比较符号换一下即可 58 min_pos = j 59 li[min_pos], li[i] = li[i], li[min_pos] 60 61 62 select_sort(l) 63 64 65 # print(l) 66 67 def insert_sort(li): 68 # 插入排序 按照我们的扑克牌排序场景进行联想, 69 for i in range(1, len(li)): # 拿到的扑克牌的下标 我们是从索引为1的值开始循环的,索引为0的值我们不循环它滤过它 70 tmp = li[i] # 我们取到的数据存入到这个变量里面, 71 j = i - 1 # 最后一个扑克牌的下标 j就是我们的for循环里面的每一个i的前一个值 72 while j >= 0 and li[j] > tmp: # 两个终止条件,j小于0表示tmp是最小的,顺序不能乱 73 """ 74 while循环的and前一个条件比较好理解就不做过多注释了,后一个我们来解释一下,我们上面的for循环里面的i是取到列表里面的每一个值, 75 然后我们的j是for循环里面的i的前一个值,如果列表里面的索引为j的值大于索引为i的值,也就是说前一个数值大于后一个数值, 76 我们就需要把大的值也就是索引为j的数值拿到后面去,从小到大的顺序排下去,前面是小的,后面是大的, 77 """ 78 li[j + 1] = li[j] # 满足上面的条件之后我们就把j赋值,j+1就是我们的j后面的值,我们给它重新赋值让它等于j,因为j是比较大的值, 79 # 大的放到后面,小的放到前面 80 j -= 1 # j每一次满足条件之后就会自动-1,然后接着去走我们的while循环,直到不满足条件之后我们就跳出while循环,去走for循环, 81 # 所以这里的j-=1是必须要存在的 82 li[j + 1] = tmp # 不满足while循环条件就走到这里来,停留在原地, 83 insert_sort(l) 84 # print(l)
堆排(组长注释版)

1 class Heap: 2 def __init__(self, sign=1): 3 self.heap = [] # 堆列表 4 self.tail = 0 # 标记堆尾 5 self.sign = sign # 标记大/小跟堆,1表示大根堆,-1表示小根堆 6 7 def _exchange_down(self, index, leaf): 8 """ 9 判断是否需要交换并下沉。 10 这是下沉函数的辅助函数,用来被考察:这个节点和他被选出的叶,是否需要交换。 11 并执行下一步下沉。 12 :param index: 考察节点 13 :param leaf: 被比较的节点 14 """ 15 if (self.heap[index] - self.heap[leaf]) * self.sign < 0: 16 self.heap[index], self.heap[leaf] = self.heap[leaf], self.heap[index] 17 self._shift_down(leaf) # 换下来的值可能不满足堆的条件,所以它需要检验下沉。 18 19 def _shift_up(self, index): 20 """ 21 上浮函数 22 :param index: 考察是否上浮的页节点 23 """ 24 father = index//2 25 if father > 0: 26 if (self.heap[index]-self.heap[father])*self.sign > 0: 27 self.heap[index], self.heap[father] = self.heap[father], self.heap[index] 28 self._shift_down(index) # 换下来的值可能不满足堆的条件,所以它需要检验下沉。 29 self._shift_up(father) # 换上去的父节点可能依然不满足堆条件,所以让他继续上浮。 30 31 def _shift_down(self, index): 32 """ 33 下沉函数: 34 :param index: 考察是否上浮的页节点 35 """ 36 leaf_l = index*2 37 leaf_r = leaf_l+1 38 if leaf_l > self.tail: # 没有页节点 39 return 40 elif leaf_r > self.tail: # 只有左叶节点 41 self._exchange_down(index, leaf_l) 42 else: # 有两个页节点 43 if (self.heap[leaf_l] - self.heap[leaf_r])*self.sign > 0: 44 self._exchange_down(index, leaf_l) 45 else: 46 self._exchange_down(index, leaf_r) 47 48 def sort(self, aim): 49 """ 50 堆排序函数。 51 更优雅:以索引1位置为整个堆的根节点。(牺牲一定的效率,可优化为以0为根) 52 这样的话。对于任意的节点,他的父节点都它索引整除2的节点。 53 它的叶就是2n和2n+1。 54 :param aim: 需要排序的列表。 55 """ 56 # 将第0个元素放在末尾。(len(aim)+1,可优化。) 57 aim.append(aim[0]) 58 self.tail = len(aim)-1 59 self.heap = aim 60 61 # 构建堆,自堆底依次上浮。 62 for i in range(len(aim)-1, 0, -1): 63 self._shift_up(i) 64 65 # 交换末尾节点和堆顶,再下沉堆被换上来的堆顶元素。 66 for i in range(len(aim)-1): 67 self.heap[1], self.heap[self.tail] = self.heap[self.tail], self.heap[1] 68 self.tail -= 1 69 self._shift_down(1) 70 71 aim.pop(0) # 最后把多余的第0个元素删除。
归并排序:

1 import random 2 3 4 def merge(li, low, mid, high): 5 """ 6 归并排序,用递归实现的, 7 先分解,不断向下二分,直至分到单个元素, 8 然后再合并,从两个元素开始合并,直至把整个列表合并完成 9 :param li: 列表参数 10 :param low: 列表起点 11 :param mid: 列表中点 12 :param high: 列表终点 13 :return: 14 """ 15 i = low # 左箭头 16 j = mid + 1 # 右箭头 17 ltmp = [] 18 while i <= mid and j <= high: 19 # 每放一个数都进行比较,直至其中一个走到尽头 20 if li[i] < li[j]: 21 ltmp.append(li[i]) 22 i += 1 23 else: 24 ltmp.append(li[j]) 25 j += 1 26 # 如果i还没有到尽头,就把i后面的元素都放进去 27 while i <= mid: 28 ltmp.append(li[i]) 29 i += 1 30 # 如果i还没有到尽头就把i后面的元素都放进去 31 while j <= high: 32 ltmp.append(li[j]) 33 j += 1 34 li[low:high + 1] = ltmp # 切片赋值 35 36 37 # 递归分解 38 def merge_sort(li, low, high): 39 if low < high: # 至少要有两个元素 40 mid = (low + high) // 2 41 merge_sort(li, low, mid) # 左边 42 merge_sort(li, mid + 1, high) # 右边 43 merge(li, low, mid, high) 44 45 46 li = [21, 52, 42, 74, 8, 9, 1, 3, 4, 6] 47 merge_sort(li,0,len(li)-1) 48 print(li)
快排:

1 import random, time, sys 2 3 sys.setrecursionlimit(1000000) 4 5 6 def cal_time(func): 7 def inner(*args, **kwargs): 8 time1 = time.time() 9 ret = func(*args, **kwargs) 10 time2 = time.time() 11 print('time:%s' % (time2 - time1)) 12 return ret 13 14 return inner 15 16 17 # 快排 18 def partition(li, left, right): 19 """ 20 先是从左边往右边找,然后再从右边往左边找,都找完替换完之后我们的排序就完成了 21 :param li: 22 :param left: 23 :param right: 24 :return: 25 """ 26 # randi = random.randint(left, right) 27 # li[randi], li[left] = li[left], li[randi] 28 29 tmp = li[left] # 取最左边的值作为中间值 30 while left < right: # 当左边的值小于右边的值的时候我们就开始进入这个while循环 31 while left < right and li[right] >= tmp: # 当我们取到的最左边的索引值小于最右边的索引值的时候 32 # 同时还要满足我们的最右边的数值大于我们的所选取的最左边的数值我们就把我们右边的数值每一次循环-1,不断向左边移动,在循环中继续判断 33 right -= 1 34 li[left] = li[right] # 当跳出循环的时候就是我们的左边的值等于右边的值的时候,两个值就重合了 35 while left < right and li[left] <= tmp: # 这里是又一层循环,跟上面的逻辑是一样的,就是我们从左边开始往右边找, 36 # 一旦我们循环到的值比我们的最左边的值小,就每一次都让left+1,不断向右边移动, 37 left += 1 38 li[right] = li[left] # 直到循环完成后我们的left和right重合,跳出循环,跳出循环之后我们的索引都已经改变了,排序已经完成了 39 li[left] = tmp # 这里我们的left在排序之后,索引位置已经发生了改变, 40 # 而我们的tmp则是一开始在上面函数中传入的形参的left一开始被赋值的值这个tmp是没有变的,我们在排序之后要让我们的left被赋值给它一开始的值 41 print(left) 42 return left # 这里我们返回left索引值,整个排序就完成了 43 44 45 def _quick_sort(li, left, right): 46 """ 47 这里我们把它改写成静态方法,然后在下面的函数中调用这里的静态方法, 48 :param li: 列表的长度 49 :param left: 列表的最左端 50 :param right: 列表的最右端 51 :return: 52 """ 53 if left < right: 54 mid = partition(li, left, right) 55 _quick_sort(li, left, mid - 1) 56 _quick_sort(li, mid + 1, right) 57 58 59 @cal_time 60 def quick_sort(li): 61 return _quick_sort(li, 0, len(li) - 1) 62 63 64 li = list(range(100, 0, -1)) # 这里是倒序 65 li1 = [2, 5, 3, 4, 7, 8, 9] 66 quick_sort(li1) 67 # print('hello',li1)
希尔排序:

1 import random 2 3 """ 4 希尔排序 5 将元素分为a个组,每组相邻两个元素之间的距离为a,在各组内进行直接插入排序 6 取第二个整数b=a/2,重复上述分组排序过程,直至n/2=1,即所有的元素在同一组内进行直接插入排序 7 """ 8 9 10 def insert_sort_gap(li, gap): 11 """ 12 这里就是我们的插入排序的逻辑代码就是多了一个参数, 13 这个参数是我们的希尔里面的那个整数,它在不断变化拆分我们的列表,然后把列表进行插入排序 14 :param li: 列表 15 :param gap: 拆分列表的参数 16 :return: 返回的是我们的插入排序后的结果 17 """ 18 for i in range(1, len(li)): 19 tmp = li[i] 20 j = i - gap 21 while j >= 0 and li[j] > tmp: 22 li[j + gap] = li[j] 23 j -= gap 24 li[j + gap] = tmp 25 26 27 def shell_sort(li): 28 d = len(li) // 2 29 while d > 0: 30 insert_sort_gap(li, d) 31 d = d // 2 # 这里的整数d不断//2,在列表中不断拆分元素,然后调用插入排序的逻辑代码 32 33 34 li = list(range(100)) 35 random.shuffle(li) 36 # print(li) 37 shell_sort(li) 38 print(li)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号