CSP-S模拟16（points given 场）

这里是下发文件（密码为比赛密码）

A. 猜道路

场切题.

可以想到的暴力做法（我想不到）当然是把每一个边的权删除，跑一遍最短路，看一下它两个点间的最短路是否比它大. 比它大，说明删除的这个边一定是一个单独的边，累加答案；相等，说明有其他边产生贡献，不管；比它小，那都不是最短路，肯定不合法输出 -1 去了.

这样就能免费水到 56 分. （逃

Time Limit Exceeded      56

既然都想到这了，那么可以发现，我把 floyed 改一下不就好了吗！

显然，既然其它边都是最短路径（因为不是最短路径在 floyed 的时候也会更新成最短路径）把每一个边的 dis 值按照原始图中的边权大小更新，不更新每一条边自己的（因为上面说了，为了判断合法及是否累计贡献），一遍最短路即可在 n³ 内解决.

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define rll rg ll
#define maxn 301
#define pll pair<ll,ll>
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
// struct node
// {
// 	ll st,ed,v;
// 	inline friend bool operator<(rg node a,rg node b) { if(a.v==b.v) { if(a.st==b.st) return a.ed<b.ed; return a.st<b.st; } return a.v<b.v; }
// }a[maxn*maxn];
ll n,ans;// ,cnt;
ll mp[maxn][maxn];
ll d[maxn][maxn];
// ll dis[maxn];
// priority_queue<pll,vector<pll>,greater<pll> > q;
// inline void dijkstra(rll x)
// {
// 	memset(dis,0x3f,sizeof(dis));q.push((pll) { dis[x]=0,x });
// 	while(!q.empty())
// 	{
// 		rll t=q.top().second;q.pop();
// 		for(rll i=1;i<=n;i++) if((i^t)&&dis[i]>dis[t]+mp[t][i]) q.push((pll) { dis[i]=dis[t]+mp[t][i],i });// ,cout<<t<<' '<<i<<' '<<dis[t]<<' '<<mp[t][i]<<endl;
// 	}
// }
inline void floyed()
{
	memset(d,0x3f,sizeof(d));// for(rll i=1;i<=n;i++) d[i][i]=0;
	for(rll k=1;k<=n;k++) for(rll i=1;i<=n;i++) for(rll j=1;j<=n;j++) if((i^j)&&(j^k)&&(i^k)&&d[i][j]>mp[i][k]+mp[k][j]) d[i][j]=mp[i][k]+mp[k][j];
}
int main()
{
	// ans=-1;if(!~ans) puts("1");
	n=read();for(rll i=1;i<=n;i++) for(rll j=1;j<=n;j++) mp[i][j]=read();
	floyed();
	for(rll i=1;i<=n;i++)
	{
		for(rll j=i+1;j<=n;j++)
			// cout<<d[i][j]<<' ';
			if(d[i][j]>mp[i][j]) ans+=mp[i][j];
			else if(d[i][j]<mp[i][j]) { ans=-1; break; }
		if(!~ans) break;
		// cout<<endl;
	}
	// for(rll i=1;i<=n;i++) for(rll j=i+1;j<=n;j++) a[++cnt]=(node){i,j,mp[i][j]};sort(a+1,a+cnt+1);
	// for(rll i=1,p;i<=n;i++)
	// {
	// 	for(rll j=i+1;j<=n;j++)
	// 	{
	// 		p=mp[i][j];mp[i][j]=mp[j][i]=0x3f3f3f3f;dijkstra(i);
	// 		// cout<<i<<' '<<j<<' '<<p<<' '<<dis[j]<<endl;
	// 		if(dis[j]>p) ans+=p;else if(dis[j]<p) { ans=-1; break; }
	// 		mp[i][j]=mp[j][i]=p;
	// 	}
	// 	if(!~ans) break;
	// }
	write(ans);
	return 0;
}

Accepted      100

B. 简单环

暴力做法显然，枚举每一条边，从一个端点进行 dfs 操作，查看是否多次遍历到另一个端点，是则跳过、不是则累加边数.

点击查看代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 100001
#define pll pair<ll,ll>
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
ll n,m;
vector<pll> g[maxn];
vector<ll> ans;
pll e[maxn];
bool flag[maxn],fl,fl2;
inline void dfs(rll x,rll fa,rll goal,rll id)
{
	if(x==goal) { if(!fl) fl=1;else fl2=1;return; }
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].first;if((g[x][i].second==id)||to==fa||flag[to]) continue;
		/*cout<<x<<' '<<to<<endl;*/flag[to]=1;dfs(to,x,goal,id);flag[to]=0;if(fl2) return;
	}
}
int main()
{
	n=read();m=read();for(rll i=1,u,v;i<=m;i++) g[u=read()].push_back((pll) { v=read(),i }),g[v].push_back((pll) { u,i }),e[i]=(pll){u,v};
	for(rll i=1;i<=m;i++)
	{
		fl=fl2=0;flag[e[i].first]=1;dfs(e[i].first,0,e[i].second,i);flag[e[i].first]=0;if(fl^fl2) ans.emplace_back(i);
	}
	write(ans.size());putn;for(rll i=0;i<ans.size();i++) write(ans[i]),put_;
	return 0;
}

52 分就到手了.

对于正解，发现它让求的其实就是点双连通分量，所以先跑个 tarjan 的点双版，然后把每一组大小非 1 的点双存一下. 之后遍历一下，由于简单环中一定是点数等于边数（除去环外的），所以每次枚举的时候判断一下即可.

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define rll rg ll
#define ull unsigned ll
#define maxn 200010
#define base 131
#define pll pair<ll,ll>
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
ll n,m;
vector<pll> g[maxn];
vector<ll> num[maxn];
set<ll> bel[maxn],ans;
ll dfn[maxn],low[maxn],cnt,tot;
bool fl[maxn];
stack<ll> s;
inline void tarjan(rll x,rll fa)
{
	dfn[x]=low[x]=++cnt;s.push(x);fl[x]=1;rg bool first=1;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].first; if(first&&to==fa) { first=0; continue; }
		if(!dfn[to])
		{
			tarjan(to,x);low[x]=min(low[x],low[to]);
			if(dfn[x]<=low[to])
			{
				bel[x].insert(++tot);num[tot].push_back(x);rll t;
				do { t=s.top();s.pop();fl[t]=0;bel[t].insert(tot);num[tot].push_back(t); } while(t^to);
			}
		}
		else low[x]=min(low[x],dfn[to]);
	}
}
int main()
{
	n=read();m=read();for(rll i=1,u,v;i<=m;i++) g[u=read()].push_back((pll) { v=read(),i }),g[v].push_back((pll) { u,i });
	for(rll i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
	for(rll i=1,sum;i<=tot;i++)
	{
		sum=0;
		for(rll j=0;j<num[i].size();j++)
			for(rll k=0;k<g[num[i][j]].size();k++) { rll to=g[num[i][j]][k].first;if(bel[to].count(i)) sum++; }
		// cout<<sum<<endl;
		if((sum>>1)==num[i].size()) for(rll j=0;j<num[i].size();j++)
			for(rll k=0;k<g[num[i][j]].size();k++) { rll to=g[num[i][j]][k].first;if(bel[to].count(i)) ans.insert(g[num[i][j]][k].second); }
	}
	write(ans.size());putn; for(rg set<ll>::iterator i=ans.begin();i!=ans.end();i++) write(*i),put_;
	return 0;
}

我表示本人并不会 FFT，所以不改 T3

暴力分的话，暴力匹配字符串，特判一下 a 串只有 0/1、b 串只有 1/0 的情况，就有了 80 分.

白送 80 有人都不要.

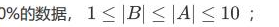
点击查看代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 1000001
#define pll pair<ll,ll>
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
ll lena,lenb,ans=INT_MAX,t;
bool fl1,fl2,fl3,fl4;
char a[maxn],b[maxn];
int main()
{
	scanf("%s",a+1);scanf("%s",b+1);fprintf(stderr,"%d %d",lena=strlen(a+1),lenb=strlen(b+1));
	for(rll i=1;i<=lena;i++) {if(a[i]^'0') fl2=1;else fl1=1;if(fl1&&fl2) break;}
	for(rll i=1;i<=lenb;i++) {if(b[i]^'0') fl4=1;else fl3=1;if(fl3&&fl4) break;}
	if(fl1&&(!fl2)&&fl3&&(!fl4)||fl2&&(!fl1)&&fl4&&(!fl3)) {puts("0");return 0;}
	if(fl1&&(!fl2)&&fl4&&(!fl3)||fl2&&(!fl1)&&fl3&&(!fl4)) {write(lenb);return 0;}
	for(rll st=0;st<=lena-lenb;st++)
	{
		t=0; for(rll i=1;i<=lenb;i++) if(a[st+i]^b[i]) t++; ans=min(ans,t);
	}
	write(ans);
	return 0;
}

D. 勇者的后缀

暂咕（需要主席树不想打）