加载中…

返回上一页
1Liu's Blog
首页 我的随笔 常用链接 联系我 留言板 友情链接 订阅 管理后台

CSP-S模拟2

题目内容 下发文件和题解

A.谜之阶乘

发现一个有趣的性质：因为阶乘的增长速率极大，因此b-a不会很大（最大也就20左右）. 因此可以暴力枚举d=b-a，那么必然有 和 . 那么最多也就只有d个可能的a，直接暴力乘，验证是否与n相等即可.

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
#define ld  double
#define rg register
#define rll rg ll
#define maxn 10000001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|48);
}
struct node
{
	ll a,b;
	inline friend bool operator<(rg node a,rg node b)
	{
		return a.a<b.a;
	}
}c[maxn];
ll t,n,ans;
int main()
{
	t=read();
	while(t--)
	{
		n=read();if(n==1) { puts("-1"); continue; }
		rll dm=20;
		c[ans=1]=(node){n,n-1};
		for(rll d=2,a,b;d<=63;d++)
		{
			b=pow((ld)n,(ld)1/(ld)d);
			while(1)
			{
				a=b-d+1;rll k=1;
				for(rll i=a;i<=b;i++) k*=i;
				if(k>n) break;
				if(k==n) { c[++ans]=(node){b,a-1}; break; }
				b++;
			}
		}
		write(ans);putn;
		for(rll i=ans;i;i--) write(c[i].a),put_,write(c[i].b),putn;
	}
	return 0;
}

B.子集

k=1时显然只有一组，直接输出即可.

记p=n/k，当n=k时显然无解. 如果n为偶数且p为奇数，那么1-n的和肯定不是k的倍数，显然也无解. 特判即可.

m为偶数时，把每一个的i与n-i配对，即：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

（相同颜色的配对）

n和m都是奇数时，前面的(p-3)k个数仍然可以用这个方法，后面的3k个数按照这个顺序排列：

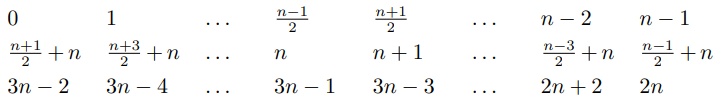
即第一行从左到右，第二行先右半部分从左到右、再左半部分从左到右，第三行先右半部分从左到右选择偶数、再左半部分从左到右选择奇数. 证明可以手模一下.

点击查看代码 
#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 1000001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|'0');
}
ll t,n,k,p;
vector<ll> g[maxn];
int main()
{
	t=read();
	while(t--)
	{
		for(rll i=1;i<maxn;i++) g[i].clear();
		n=read();k=read();p=n/k;
		if(k==1) { puts("Yes"); for(rll i=1;i<=n;i++) write(i),put_; putn; continue; }
		if(n==k||p==1||((!(n&1))&&(p&1))) { puts("No"); continue; }
		// k：组数	p：每组个数
		puts("Yes");
		if(p&1)
		{
			for(rll i=1,l;i<=(p-3>>1);i++)
			{
				l=(i-1<<1)*k;
				for(rll j=1;j<=k;j++) g[j].push_back(l+j);
				for(rll j=k;j;j--) g[j].push_back(l+k+k-j+1);
			}
			rll l=(p-3)*k;
			for(rll i=1;i<=k;i++) g[i].push_back(l+i);
			l+=k;
			for(rll i=(k-1>>1)+1;i<=k;i++) g[i].push_back(l+i-(k-1>>1));
			for(rll i=1;i<=(k-1>>1);i++) g[i].push_back(l+k-(k-1>>1)+i);
			for(rll i=(k-1>>1)+1,p=n;i<=k;i++,p-=2) g[i].push_back(p);
			for(rll i=1,p=n-1;i<=(k-1>>1);i++,p-=2) g[i].push_back(p);
			for(rll i=1;i<=k;i++)
			{
				for(rll j=0;j<g[i].size();j++) write(g[i][j]),put_;
				putn;
			}
		}
		else
		{
			for(rll i=1,l;i<=k;i++)
			{
				for(rll j=1;j<=(p>>1);j++)
					l=j-1<<1,write(l*k+i),put_,
					write((l|1)*k+k-i+1),put_;
				putn;
			}
		}
	}
	return 0;
}

C.混凝土粉末

按照题解所述一步一步做即可.

询问本质是：作若干次区间加，并询问 x 位置上的值最早 ≥ y 的时间.
将询问离线，并在序列下标上执行扫描线，开一棵以询问编号为下标的树状数组.
扫描到一个修改的左端点时，在树状数组上这个修改的标号位置加上，扫到右端点时减去.
扫描到一个询问时，在树状数组上二分即可.

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
#define rg register
#define ld double
#define rll rg ll
#define pll pair<ll,ll>
#define maxn 2000001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|'0');
}

template<typename T,size_t siz>
class bit
{
private:
#define lowbit(x) (x&-x)
	ll c[siz];
public:
	inline void add(ll x,ll n,ll v)
	{
		for(rll i=x;i<=n;i+=lowbit(i)) c[i]+=v;
	}
	inline ll query(ll x)
	{
		rll ans=0;
		for(rll i=x;i;i-=lowbit(i)) ans+=c[i];
		return ans;
	}
#undef lowbit
};
ll n,q,op[maxn],l,r,p,x,y;
bit<ll,maxn> t;
vector<pll> g[maxn],h[maxn];
ll ans[maxn];
static inline bool chk(rll i,rll mid)
{
	return t.query(mid)>=i;
}
int main()
{
	n=read();q=read();
	for(rll i=1;i<=q;i++)
	{
		op[i]=read();
		switch(op[i])
		{
		case 1:
			l=read();r=read();p=read();
			g[l].push_back((pll) { i,p });g[r+1].push_back((pll) { i,-p });
			break;
		case 2:
			x=read();y=read();
			h[x].push_back((pll) { i,y });
			break;
		}
	}
	for(rll i=1;i<=n;i++)
	{
		for(rll j=0;j<g[i].size();j++) t.add(g[i][j].first,q,g[i][j].second);
		for(rll j=0;j<h[i].size();j++)
		{
			rll l=1,r=h[i][j].first,mid,num;
			while(l<r)
			{
				mid=(l+r)>>1;
				if(chk(h[i][j].second,mid)) ans[h[i][j].first]=r=mid;
				else l=mid+1;
			}
		}
	}
	for(rll i=1;i<=q;i++) if(op[i]==2) write(ans[i]),putn;
	return 0;
}

D.排水系统

有一个性质，如果一个点的管道堵塞，那么从这个点经过的污水吨数一定不变. 那么可以发现，如果管道(x,y)堵塞，那么就可以把其视作经过y的污水吨数减少一个值、经过x的其它出点的污水吨数增加一个值. 那么增加或减少t吨的污水就可以看成这个点初始有x或者-x吨污水，先处理初始有的污水，再来一次拓扑排序即可.

那么发现y增加的污水可以转换到x增加的污水，这样复杂度就由n方变成了n+k.

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
#define rg register
#define rll rg ll
#define pll pair<ll,ll>
#define maxn 500001
#define put_ putchar(' ')
#define putn putchar('\n')
#define mod 998244353
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|'0');
}
ll n,m,r,k;
ll sum,x[maxn],y[maxn],a[maxn];
ll dp[maxn],f[maxn],cd[maxn],du1[maxn],du2[maxn];
vector<pll> g[maxn];
queue<ll> q;
static inline ll ksm(rll a,rll b)
{
	rll ans=1;a%=mod;for(rll i=b;i;i>>=1) { if(i&1) ans=ans*a%mod; a=a*a%mod; }return ans;
}
int main()
{
	n=read();m=read();r=read();k=read();
	for(rll i=1;i<=k;i++)
		x[i]=read(),y[i]=read(),a[i]=read(),
		cd[x[i]]++,du1[y[i]]++,du2[y[i]]++,
		g[x[i]].push_back((pll) { y[i],a[i] }),sum=(sum+a[i])%mod;
	sum=ksm(sum,mod-2);
	for(rll i=1;i<=m;i++) q.push(i),dp[i]=1;
	while(!q.empty())
	{
		rll t=q.front();q.pop();
		for(rll i=0;i<g[t].size();i++)
		{
			dp[g[t][i].first]=(dp[g[t][i].first]+dp[t]*ksm(cd[t],mod-2)%mod)%mod;
			du1[g[t][i].first]--;if(!du1[g[t][i].first]) q.push(g[t][i].first);
		}
	}
	for(rll i=1;i<=k;i++)
		f[x[i]]=(f[x[i]]+dp[x[i]]*ksm(cd[x[i]]-1,mod-2)%mod*a[i]%mod*sum%mod)%mod,
		f[y[i]]=(f[y[i]]-dp[x[i]]*ksm(cd[x[i]]-1,mod-2)%mod*a[i]%mod*sum%mod+mod)%mod;
	for(rll i=1;i<=n;i++)
		if(i<=m) f[i]=(f[i]+1)%mod,q.push(i);
	while(!q.empty())
	{
		rll t=q.front();q.pop();
		for(rll i=0;i<g[t].size();i++)
		{
			f[g[t][i].first]=(f[g[t][i].first]+f[t]*ksm(cd[t],mod-2)%mod)%mod;
			du2[g[t][i].first]--;if(!du2[g[t][i].first]) q.push(g[t][i].first);
		}
	}
	for(rll i=n-r+1;i<=n;i++) write(f[i]),put_;
	return 0;
}
posted @ 2022-09-04 19:59  1Liu  阅读(34)  评论(0)    收藏  举报