CSP-S模拟1

下发文件和题解

A. 斐波那契

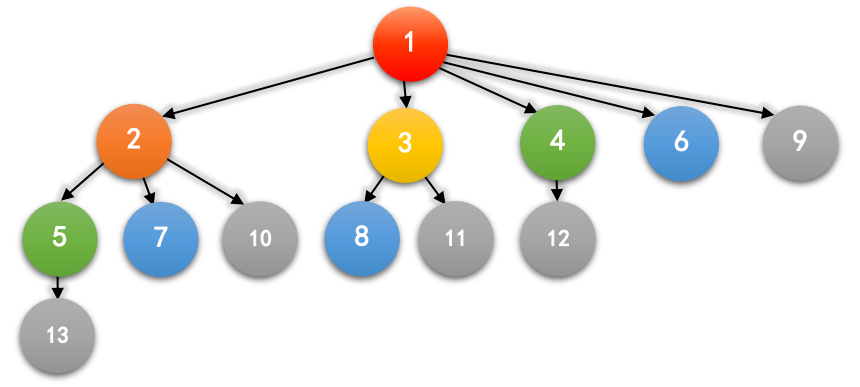
对于上面这张图，尝试从2开始依次写下每个兔子的父亲的标号：

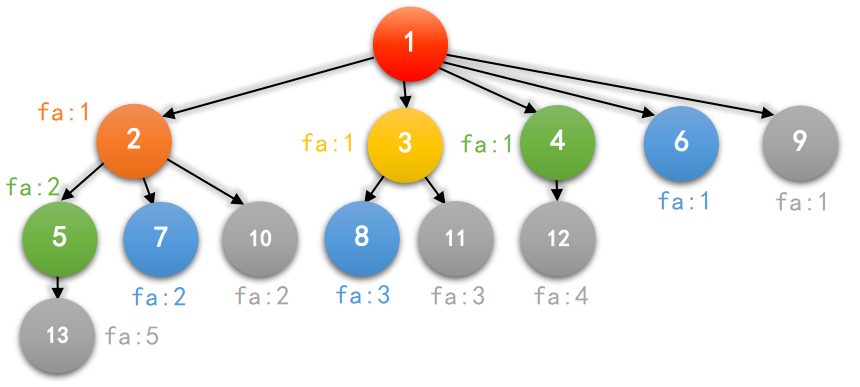
那么转换成数列就是这样的：

1 1 1 2 1 2 3 1 2 3 4 5 ...

可以发现这个序列由多个连续从 1 开始的序列组合到一起，每段长度依次是斐波那契数列里面的每一项.

那么就有以下规律：

令f(i)表示第i个月总共的兔子数量，那么有f(0)=0，f(1)=1.
因为第i个月时只有第i-2个月及以前就有的兔子可以产生下一代，那么就有f(i)=f(i-1)+f(i-2).

这不就是斐波那契数列吗？

那么在第i个月出生的第j个兔子编号显然是f(i-1)+j.

然后就可以倒推它的父亲了. 一个点x的父亲即为x-f(k)，当且仅当f(k)<x≤f(k+1).

维护一个map，暴力把左边的点的所有父节点标记，再每次向上递归右边的点的父节点，直至有一个节点被标记，那么这个节点就是要求的lca. 每次找k的时候用lower_bound就可以了.

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define rll rg ll
#define maxn 1000001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|48);
}
ll m,a,b;
ll f[maxn];
map<ll,bool> g;
bool flag;
int main()
{
	f[1]=1;for(rll i=2;i<=60;i++) f[i]=f[i-1]+f[i-2];
	m=read();
	for(rll i=1;i<=m;i++)
	{
		g.clear();flag=0;
		a=read();b=read();g[a]=1;
		while(a!=1) a=a-f[lower_bound(f+1,f+61,a)-f-1],g[a]=1;
		while(b!=1)
		{
			if(g[b]) { write(b); flag=1; putn; break; }
			b=b-f[lower_bound(f+1,f+61,b)-f-1];
		}
		if(!flag) puts("1");
	}
	return 0;
}

B.数颜色

拿分块水过的，注意把块长调整到230左右就行了.

点击查看代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 300001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|48);
}
ll n,m,op,l,r,c,x;
ll a[maxn],len,st[maxn],ed[maxn],bel[maxn];
short col[550][maxn];
static inline ll query(rll l,rll r,rll c)
{
	rll ans=0;
	if(bel[l]==bel[r]) { for(rll i=l;i<=r;i++) ans+=(a[i]==c); return ans; }
	for(rll i=l;i<=ed[bel[l]];i++) ans+=(a[i]==c);
	for(rll i=bel[l]+1;i<bel[r];i++) ans+=col[i][c];
	for(rll i=st[bel[r]];i<=r;i++) ans+=(a[i]==c);
	return ans;
}
int main()
{
	n=read();m=read();len=min((ll)sqrt(n),230);
	for(rll i=1;i<=n;i++) a[i]=read();
	for(rll i=1;i<=len;i++) st[i]=n/len*(i-1)+1,ed[i]=n/len*i;ed[len]=n;
	for(rll i=1;i<=len;i++) for(rll j=st[i];j<=ed[i];j++) bel[j]=i,col[i][a[j]]++;
	while(m--)
	{
		op=read();
		switch(op)
		{
		case 1:
			l=read();r=read();c=read();
			write(query(l,r,c));putn;
			break;
		case 2:
			x=read();
			if(bel[x]!=bel[x+1]) col[bel[x]][a[x]]--,col[bel[x+1]][a[x+1]]--,col[bel[x+1]][a[x]]++,col[bel[x]][a[x+1]]++;
			swap(a[x],a[x+1]);
			break;
		}
	}
	return 0;
}

C. 分组

为了保证字典序最小，在扫的时候应该从后往前扫.

这个题在k=1和k=2的情况要分别讨论.

k=1的时候，直接扫，扫的时候判断一下当前的数是否会与上一段的数发生冲突，即出现平方的情况. 具体是要找出最长的合法分段，从后往前选择一段最长的合法区间并分割，重复进行直到完成为止. 那么需要判断的条件是 ，因为 ，所以一定有 . 枚举一下x，判断一下 是不是出现过.

k=2的时候，可以利用二分图的思想，把每一个数拆成两个点，即 、、、，把冲突的数连边，如果它符合二分图，就可以分成一组. 维护用并查集即可.

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define rll rg ll
#define maxn 270001
#define mx 512 // 需要判定条件是 x^2=a_i+a_j，那么因为 2≤a_i+a_j≤262144，所以一定有 2≤x≤512.
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|48);
}
ll n,k,m,ls;
ll f[maxn];
vector<ll> g[maxn];
ll a[maxn];
stack<ll> s;
static inline ll find(rll x)
{
	if(x!=f[x]) f[x]=find(f[x]);return f[x];
}
static inline void clear(rll x)
{
	for(rll i=ls-1;i>x;i--) g[a[i]].clear();
	ls=x+1;s.push(x);
}
int main()
{
	for(rll i=1;i<maxn;i++) f[i]=i;
	n=read();k=read();ls=n+1;
	for(rll i=1;i<=n;i++) a[i]=read(),m=max(m,a[i]);
	switch(k)
	{
	case 1:
		for(rll i=n;i;i--)
		{
			rg bool fl=0;
			for(rll j=1;j<=mx;j++)
				if(j*j>=a[i]&&(!g[j*j-a[i]].empty()))
				{
					fl=1;break;
				}
			if(fl) clear(i);
			g[a[i]].push_back(0);
		}
		break;
	case 2:
		for(rll i=n;i;i--)
		{
			for(rll j=1;j<=mx;j++)
				if(j*j>=a[i]&&(!g[j*j-a[i]].empty()))
					for(rll l=0;l<g[j*j-a[i]].size();l++)
					{
						rll fa=g[j*j-a[i]][l];
						if(find(i)==find(fa)) clear(i);
						else f[find(n+i)]=find(fa),f[find(n+fa)]=find(i);
					}
			g[a[i]].push_back(i);
		}
		break;
	}
	write(s.size()+1);putn;
	while(!s.empty()) write(s.top()),s.pop(),put_;
	putn;
	return 0;
}