CSP-S加赛0909

下发文件

A. 元素周期表

内存限制：128 MiB 时间限制：1000 ms 标准输入输出

题目类型：传统评测方式：文本比较

Innopolis 大学的教授正努力研究元素周期表.他们知道，有种元素，形成了一个行列的矩阵.

研究表明，如果元素周期表上有一个元素 A，且元素 B 与它在同一列（A 与 B 不能在同一周期），元素 C 在同一周期（A 与 C 不能在同一列），那么，科学家就可以用这三种元素通过核聚变合成第四种元素 D 的样品，D 与 B 在同一周期，与 C 在同一列.

简而言之，如果有在元素周期表中位置为（其中 ?）的三种元素的样品，就可以生成位置为的样品.如图所示：

注意：在核聚变中被使用的样品并不会消失，它们可以参与之后的反应；反应得到的样品也可以参与反应.

他们已经获得了种元素的样品.为了集齐所有元素的样品，他们会购买一些样品，然后利用核聚变制造出剩下元素的样品.

请求出他们至少需要购买的元素样品的数量.

第一行，个整数 .

之后的行，每行个整数 .保证给定的元素互不相同.

输出一个整数，表示至少需要购买的元素样品的数量.

样例输入1

样例输出1

样例输入2

样例输出2

样例输入3

样例输出3

样例解释

每个样例解释中有两个矩阵. 第一个表示初始状况（其中，打叉的是原本就有样品的元素）. 第二个表示最终集齐样品时的状况（其中，蓝圈代表核聚变得到的样品，蓝圈中的数字表示得到样品的顺序，红圈表示购买的样品）.

样例解释 1

通过给定的三种元素，可以得到第四种元素的样品.

样例解释 2

由于给定的元素只有一行，无法使用核聚变，只能购买剩余的两种元素的样品.

样例解释 3

集齐所有元素的方法不唯一，以下是一种方法.其中，元素 (4, 2)(4,2) 只有在购买元素 (4, 1)(4,1) 的样品，和反应得到元素 (1, 1)(1,1)的样品后才能得到.

注意：当且仅当你通过了一个子任务下的所有测试点，你将获得此子任务的分数.

子任务编号	分数
1	10
2	17
3	8
4	20
5	30
6	15

脑子不够，图论来凑

发现有了(x1,y1)、(x1,y2)、(x2,y1)就可以获得(x2,y2)，可以愉快地想到图论. 就是把x2和y1连边、把x1和y2连边，这样可以获得一个叉形图. 然后把x1与y1连边，你发现了什么？

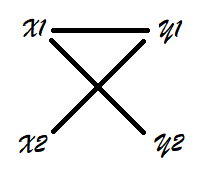
没错！就是强连通分量！

这样题目就转化为了求最少加几条边使得整个图强连通.

那就非常简单了.

点击查看代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 400001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
static inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();
	while(ch<'0'||ch>'9') f|=(ch=='-'),ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
	return f?-x:x;
}
static inline void write(rll x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);putchar(x%10|'0');
}
ll n,m,q;
vector<ll> g[maxn];
ll dfn[maxn],low[maxn],cnt,tot;
bool fl[maxn];
stack<ll> st;
inline void tarjan(ll x)
{
	dfn[x]=low[x]=++cnt;st.push(x);fl[x]=1;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i];
		if(!dfn[to]) tarjan(to),low[x]=min(low[x],low[to]);
		else if(fl[to]) low[x]=min(low[x],dfn[to]);
	}
	if(dfn[x]==low[x])
	{
		rll t;tot++;
		do { t=st.top();st.pop(); } while(t!=x);
	}
}
int main()
{
	n=read();m=read();q=read();
	for(rll i=1,r,c;i<=q;i++) r=read(),c=read(),g[r].push_back(n+c),g[n+c].push_back(r);
	for(rll i=1;i<=n+m;i++) if(!dfn[i]) tarjan(i);
	write(tot-1);
	return 0;
}

B. gcd

内存限制：256 MiB 时间限制：1000 ms 标准输入输出

题目类型：传统评测方式：文本比较

有n 个正整数x1~xn，初始时状态均为未选. 有m 个操作，每个操作给定一个编号i，将xi 的选取状态取反. 每次操作后，你需要求出选取的数中有多少个互质的无序数对.

第一行两个整数n,m.第二行n 个整数x1~xn.接下来m 行每行一个整数.

m 行，每行一个整数表示答案.

样例输入

样例输出

对于20%的数据，n,m<=1000. 对于另外30%的数据，xi<=100. 对于100%的数据，n,m<=200000，xi<=500000，1<=i<=n.

题目的大意即是给定n个数，求出这n个数中互质的无序数对的个数，且要支持修改.

对于这种个数的问题，自然会想到类似dp的做法. 那么可以尝试：
设f[i]为最大公约数为i的数对个数，
g[i]为最大公约数为i的倍数的数对个数，
s[i]为i的倍数的数字的个数.

对于s[i]可以非常轻易地求出，每次枚举的时候暴力加就行了，即枚举每一个数的约数，把这个约数的s值加1.

如何将s[i]与g[i]产生联系呢？

手模一下不难发现有以下结论：

有了g[i]，且显然已知f[i]与g[i]的关系为：

这是什么？

莫比乌斯反演！

（如果不知道莫反是什么的话还请移步先学习它，因为它在数论题解题方面非常重要，所以还是有必要一学的.）

根据莫反的性质，可以得到如下式子：

最后把1到n的f值加起来，即为答案. 发现f值其实并没有其他用处，因此可以直接计算，累加答案.