二分图

二分图是一个集合严格来说其实是两个，其中分为两部分，每一部分都是一个独立的集合（就是每一部分内部没有边互相连接）.

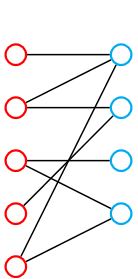
（无耻盗图）

那么能够知道，一张图是二分图，当且仅当其中不存在奇环.

可以发现，成环的时候，如果边数为奇，那么一定会有一条边处在一个部分的内部.

偶环的话可以这样：

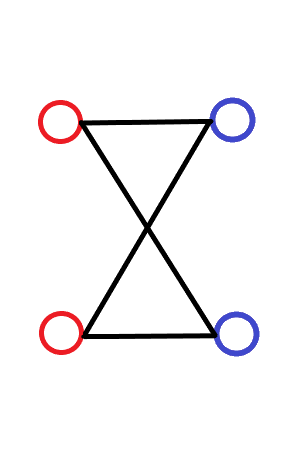
判定二分图：

染色法.

用一个数组标记其中的颜色，比如 1 是黑、2 是白. 一个点被标记后，把它的所有相邻节点标记为与它相反的颜色. 如果标记时发现存在冲突，则说明其不是二分图.

点击查看代码

ll col[maxn];
bool fl;
inline bool dfs(rll x,rll fa,rll nowc)
{
	col[x]=nowc;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i]; if(to==fa) continue;
		if((!col[to])&&(!dfs(to,x,3-nowc))) return 0;
		if(col[to]==nowc) return 0;
	}
	return 1;
}
int main()
{
	bool fl=1;
	for(rll i=1;i<=n;i++) if((!col[i])&&(!dfs(i,0,1))) { fl=0; break; }
	// fl为1表明是二分图，为0表明不是
}

最大匹配：

二分图匹配，实际上意思是一张二分图的子图中任何两条边没有公共点. 也就是说每一个点仅连着一条边.

什么是最大匹配？就是指这张二分图中具有边数最多的一个匹配.

如何去求？

每一次寻找增广路，把路径上的所有边的匹配状态进行取反. 重复操作直至无增广路.

这就是匈牙利算法.

点击查看代码

inline bool dfs(rll x)
{
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i];
		if(!vis[to])
		{
			vis[to]=1;
			if(!match[to]/*即匹配点*/||dfs(match[to]))
			{
				match[to]=x;
				return 1;
			}
		}
	}
	return 0;
}
inline ll solve()
{
	for(rll i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(dfs(i)) ans++;
	}
	return ans;
}

完美匹配：

其实就是在最大匹配的基础上要求每一个点都有连边. 不一定每一个图都有完美匹配.

最大权匹配：

暂时不写.