数学知识

~~咕了好久没有公开，今天终于公开了……~~

矩阵

什么是矩阵？

其实就是一个二维数组.~~用你说~~

矩阵乘法

就是把两个矩阵乘起来，获得一个新的矩阵.

需要注意它只满足结合律，不满足交换律.

设 A 矩阵为 n 行 m 列的矩阵，且 B 矩阵为 m 行 p 列的矩阵（因为行数列数不相同是没有乘法一说的）.

公式：

参考代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define rll rg ll
#define maxn 101
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
struct node// 封装版
{
	lla[201][201];
	node operator*(const node b)
	{
		node c;
		memset(c.a,0,sizeof(c.a));
		for(rll i=1;i<=n*10;i++)
			for(rll j=1;j<=n*10;j++)
				for(rll k=1;k<=n*10;k++)
					c.a[i][j]=(c.a[i][j]+a[i][k]*b.a[k][j])%mod;
		return c;
	}
}a;
ll a[maxn][maxn],b[maxn][maxn],c[maxn][maxn];
int main()
{
	n=read();m=read(); for(rll i=1;i<=n;i++) for(rll j=1;j<=m;j++) a[i][j]=read();
	p=read(); for(rll i=1;i<=m;i++) for(rll j=1;j<=p;j++) b[i][j]=read();
	for(rll i=1;i<=n;i++) for(rll j=1;j<=p;j++) for(rll k=1;k<=m;k++) c[i][j]+=a[i][k]*b[k][j];
	for(rll i=1;i<=n;i++)
	{
		for(rll j=1;j<=p;j++) write(c[i][j]),put_;
		putn;
	}
	return 0;
}

矩阵快速幂

利用快速幂的性质，可以将其推广到矩阵上.

点击查看代码

inline ll ksm(rg node a,rll t)
{
	rg node ans=a;
	for(rll i=t;i;i>>=1) { if(i&1) ans=ans*a;a=a*a; }
	return ans.a[1][n];
}

高斯消元

线性方程组：

其实就是一堆一次方程组合到了一起.

高斯消元是把每一个线性方程组放到矩阵里，每一次进行消元.

系数矩阵：就是把方程的每一个系数提出来，放在对应的位置（例如 x₁ 的系数放在第 1 个位置，x₂ 的系数放在第 2 个位置）.

增广矩阵：向系数矩阵后面加一列，表示每个方程等号右边的常数.

比如这个方程：

，

化为增广矩阵就是：

如何判断是否有解？

如果前面的方程加和后与后面的方程冲突（系数同常数项不同），那么一定无解. 废话

如果系数同常数项也同，那么该方程有多解.

其余情况只有一解.

怎么解？

每次把一个未知数的系数消为 0，只剩下一个方程的这位系数不为 0.

具体来说：设当前消到了第 i 位，那么就把从第 i + 1 位开始所有的这一位进行代入，把它的系数消为 0.

这样一个方程组就被消成了个倒三角的形状.

（随便拉过来一张图作展示）

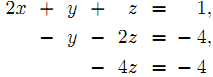
然后，就是……

从下往上把每一位消掉！

下面是代码：

点击查看代码

#include<bits/stdc++.h>
#define ll int
#define rg register
#define ld double
#define rll rg ll
#define maxn 51
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
ll n,now=1;//now是现在消到了第几行
ld a[maxn][maxn];
int main()
{
	n=read(); for(rll i=1;i<=n;i++) for(rll j=1;j<=n+1;j++) a[i][j]=read();
	//第i+1列存的是等号后的数值
	for(rll l=1;l<=n;l++)//第几列
	{
		rll mx=now; for(rll i=now+1;i<=n;i++) if(abs(a[i][l])>abs(a[mx][l])) mx=i;
		if(!a[mx][l]) continue; for(rll i=1;i<=n+1;i++) swap(a[now][i],a[mx][i]);
		//把当前行和元系数最大的行交换
		for(rll i=1;i<=n;i++)//消元过程
		{
			if(i==now) continue; rg ld t=a[i][l]/a[now][l];//找到能消的最大系数
			for(rll j=l+1;j<=n+1;j++) a[i][j]-=a[now][j]*t;
		}
		now++;//所在行+1
	}
	if(now<n+1)//因为最后多加了个1
	{
		while(now<n+1) { if(a[now][n+1]) { puts("-1");return 0; } now++; }
		puts("0"); return 0;
	}
	for(rll i=1;i<=n;i++)
	{
		putchar('x');write(i);putchar('=');
		if(!(ll)(a[i][n+1]/a[i][i]*100)) puts("0.00");
		else printf("%.2lf\n",a[i][n+1]/a[i][i]);
	}
	return 0;
}

数论基础

素数

就是质数.

定义一个数是素数，当且仅当它是除 1 以外的正整数且它的因数只有 1 和它本身.

筛法求素数

埃氏筛

枚举每个 i，然后枚举它的倍数，将它们设为非素数. 对于后面是非素数的，就不再枚举了.

实现：

点击查看代码

inline void shai()
{
	notp[1]=1;
	for(rll i=2;i<maxn;i++) if(!notp[i])
		for(rll j=2;i*j<maxn;j++) notp[i*j]=1;
}

线性筛

每个非素数由它的最小质因子筛掉.

实现：

点击查看代码

ll prime[maxn],cnt;
bool notp[maxn];
inline void xxs()
{
	notp[1]=1;
	for(rll i=2;i<=n;i++)
	{
		if(notp[i]) prime[++cnt]=1;
		for(rll j=1;j<=cnt&&i*prime[j]<=n;j++)
		{
			notp[i*prime[j]]=1;
			if(!(i%prime[j])) break;// 每个合数只需要被筛一次
		}
	}
}

筛法求欧拉函数和莫比乌斯函数

下面有讲.

同余

顾名思义，就是当在同一个模数下两个数对于这个数取模后的结果是相同的.

记作：a ≡ b (mod m).

性质的话都很简单，先不说了.

逆元

乘法逆元常用来解决在模数意义下除法的问题.

一般用来求逆元的方法有两种：

费马小定理

它是借助乘法快速幂实现的.

当模数 p 为素数时，一个数在模其意义下的乘法逆元是这个数的模数减二次方.

由于是复习，具体证明就不再细说.

实现：

点击查看代码

inline ll ksm(rll a,rll b)
{
	rll ans=1; a%=mod;
	for(rll i=b;i;i>>=1)
	{
		if(i&1) ans=ans*a%mod; a=a*a%mod;
	}
	return ans;
}

ny=ksm(n,mod-2);

扩展欧几里得定理

求最大公约数

辗转相除法. 每次将 a 变为 b，然后使 b 变为 a % b. 其可用递归或者 while 循环实现.

点击查看代码

inline ll gcd(rll a,rll b) { if(!b) return a; return gcd(b,a%b); }

将其扩展一下：

我们知道，在模 p 意义下，一个数 a存在乘法逆元当且仅当 gcd(a , p) = 1.

这个定理常用来解方程 ax + by = gcd(a , b)中 x，y 的整数解.

那么就有为 a 模 b 的乘法逆元，y 为 b 模 a 的乘法逆元.

点击查看代码

inline ll exgcd(rll a,rll b,rll& x,rll& y)
{
	if(!b) { x=1; y=0; return a; }
	rll ans=exgcd(b,a%b,x,y),t=x; x=y;y=t-a/b*y;
	return ans;
}
// 求出来的x即为逆元

欧拉函数

欧拉函数指的是对于一个数 n，小于等于它的数中与它互质的数的个数.

公式：

，

其中 p_i 为 n 的所有质因数.

性质（搬的）：

φ(1)=1；

若 p 是一个素数，则 φ(p)=p−1；

若 p 是一个素数，则 φ(p^k)=(p−1)×p^k−1；

欧拉函数为积性函数：对于任意两个正整数 a,b，且 gcd(a,b)=1，则 φ(a×b)=φ(a)×φ(b). 特别的，对于奇数 n，φ(2n)=φ(n).

如何求欧拉函数？

求单个数的欧拉函数

在分解质因数的同时去求即可.

点击查看代码

inline ll phi(rll x)
{
	rll n=ceil(sqrt(x)),ans=x;
	for(rll i=2;i<=n;i++) if(!(x%i))
	{
		ans=ans/i*(i-1);
		while(!(x%i)) x/=i;
	}
	if(x>1) ans=ans/x*(x-1); return ans;
}

用线性筛求多个数的欧拉函数

点击查看代码

ll phi[maxn];
inline void shai()
{
	for(rll i=1;i<maxn;i++) phi[i]=i;
	for(rll i=2;i<maxn;i++) if(phi[i]==i) for(rll j=i;j<maxn;j+=i) phi[j]=phi[j]*(i-1)/i;
}

排列组合

排列：n 个数以不同的顺序出现在数列中.

从 n 个数中选择 m 个数进行有序排列，总共的方案数为 .

求总共排列数的方法：

组合：n 个数无序地分在一起.

从 n 个数中选择 m 个数进行无序组合，总共的方案数为 .

求总共组合数的方法：

求排列组合数的实现：

点击查看代码

ll jc[maxn];
inline ll A(rll n,rll m)
{
	if(n<m) return 0;
	return jc[n]/jc[n-m];
}
inline ll C(rll n,rll m)
{
	if(n<m) return 0;
	return jc[n]/jc[m]/jc[n-m];
}

阶乘这玩意太大，需要取模. 把除换成快速幂即可.

点击查看代码

ll jc[maxn];
inline ll ksm(rll a,rll b)
{
	rll ans=1;a%=p;
	for(rll i=b;i;i>>=1)
	{
		if(i&1) ans=ans*a%p;
		a=a*a%p;
	}
	return ans;
}
inline ll A(rll n,rll m)
{
	if(n<m) return 0;
	return jc[n]*ksm(jc[n-m],p-2)%p;
}
inline ll C(rll n,rll m)
{
	if(n<m) return 0;
	return jc[n]*ksm(jc[m],p-2)%p*ksm(jc[n-m],p-2)%p;
}

Lucas 定理

内容：

实现：

点击查看代码

inline ll lucas(rll a,rll b)
{
	if(!b) return 1;
	return C(a%mod,b%mod)*lucas(a/mod,b/mod)%mod;
}

容斥原理

先扔个式子：

点击查看代码

$\left|\bigcup\limits_{i=1}^{n}S_i\right|=\sum\limits_{i=1}^{n}\left|S_i\right|-\sum\limits_{1\le i<j\le n}\left|S_i\cap S_j\right|+\sum\limits_{1\le i<j<k\le n}\left|S_i\cap S_j\cap S_k\right|+\cdots+\left(-1\right)^{n+1}\left|S_1\cap\cdots\cap S_n\right|$

举个例子很好理解：

假如我们要算 A ∪ B ∪ C，那么计算方法一定是 A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C.

做题时经常用到.比如要计算 (x₁ , y₁) 到 (x₂ , y₂) 的面积，那么就用 (x₂ , y₂) 的和减去 (x₁ - 1 , y₂) 减去 (x₂ , y₁ - 1)，最后加上 (x₁ - 1 , y₁ - 1).

中国剩余定理（CRT）

它用来求解一个一元线性同余方程组.

例如如下方程组：

如何计算？

首先，计算所有模数的乘积，设它为 a；

然后，对于第 i 个方程：

先计算出 m = ，然后计算 m 在模 n_i 意义下的逆元，然后计算，方程的唯一解为 .

实现：

点击查看代码

inline ll crt(ll n)//中国剩余定理
{
	rll t=1,ans=0;
	for(rll i=1;i<=n;i++) t*=b[i];
	for(rll i=1;i<=n;i++)
	{
		rll m=t/b[i],x,y;
		gcd(m,b[i],x,y);
		ans=(ans+a[i]*m*x%t)%t;
	}
	return (ans%t+t)%t;
}

BSGS

用来解高次同余方程 a^x ≡ b (% p).

不是 noip 要求掌握的东西，懒得写了.

搬一个模板题的链接

posted @ 2022-10-05 16:15 1Liu 阅读(10) 评论(0) 收藏举报

刷新页面返回顶部

1Liu's Blog

进学致和，行方思远.

数学知识

矩阵

矩阵乘法

矩阵快速幂

高斯消元

数论基础

素数

埃氏筛

线性筛

筛法求欧拉函数和莫比乌斯函数

同余

逆元

费马小定理

扩展欧几里得定理

欧拉函数

排列组合

Lucas 定理

容斥原理

中国剩余定理（CRT）

BSGS

公告