强连通分量、缩点

强连通分量

啥叫强连通分量？

一般来讲，一张有向图的子图是强连通分量，当且仅当其内部任意一个点可以到达另外任意一个点.

如何求？

dfn[x]：点x的访问时间，也是反拓扑序；
low[x]：点x的后面遍历到的点里在栈中最早节点的时间戳

模板：

inline void tarjan(rll x)
{
	dfn[x]=low[x]=++cnt;
	fl[x]=1;s.push(x);
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].first;
		if(!dfn[to]) tarjan(to),low[x]=min(low[x],low[to]);
		else if(fl[to]) low[x]=min(low[x],dfn[to]);
	}
	if(dfn[x]==low[x])
	{
		rll t;tot++;
		do
		{
			t=s.top();s.pop();fl[t]=0;
			belong[t]=tot;num[tot]++;
		} while(t!=x);
	}
}

无向图上的 Tarjan

求割

求割点

什么是割点：

割点如果被删除，原来的连通图会分裂成多个子图.

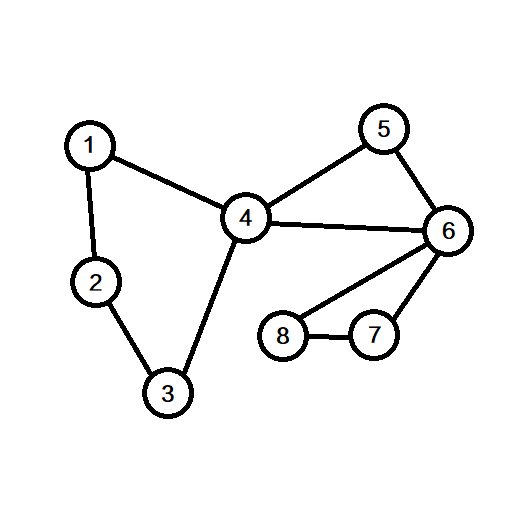
图中点 4 即为割点.

实现：

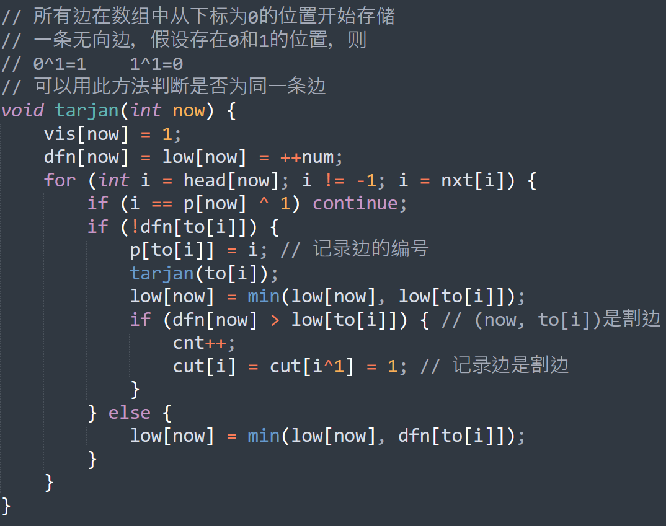
inline void tarjan(rll x)
{
	dfn[x]=low[x]=++cnt; rll son=0;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].first;
		if(!dfn[to])
		{
			son++;tarjan(to);low[x]=min(low[x],low[to]);
			if(dfn[x]<=low[to]) if((x^rt/*dfs搜索树起点*/)||son>1) cut[x]=1;
			// 如果是搜索起点至少需要两棵子树才能成为割点
		}
		else low[x]=min(low[x],dfn[to]);
	}
}

求割边

什么是割边：

就是这个边被删除，原来的连通图也会分裂.

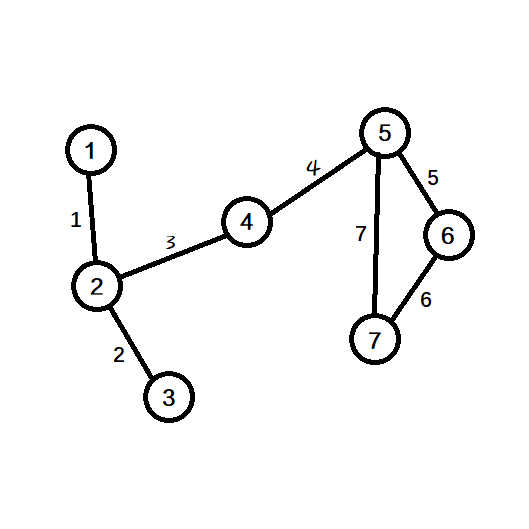
边 3 和 4 均为割边.

实现：

1. 判断 low[to]=dfn[to]

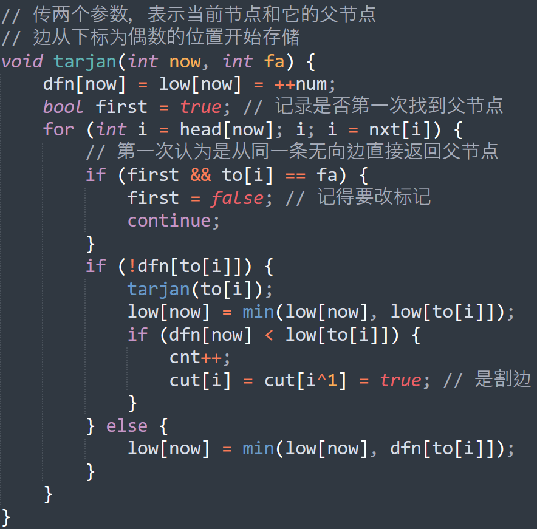
inline void tarjan(rll x)
{
	dfn[x]=low[x]=++cnt; fl[x]=1;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].to;
		// 子节点没有被访问过，直接递归访问
		if(!dfn[to])
		{
			p[to]=g[x][i].id;
			tarjan(to);low[x]=min(low[x],low[to]);
		}
		// 从子节点递归上来找到了父亲，判断一下编号，如果和从它前面节点（父亲）回来的编号一样，就不能走，防止重复递归
		else if(p[x]^g[x][i].id) low[x]=min(low[x],dfn[to]);
	}
	if(p[x]&&dfn[x]==low[x]) cut[p[x]]=1;
}

2. 判断 dfn[x]<low[to]

课件上的，懒得打了，反正也不常用.

3. 综合判断

一样是课件上的

求双连通分量

求点双

点双是一个子图，其内部不存在割点.

就是找割点，在栈里割点上面的点的集合就是一个点双.

inline void tarjan(rll x,rll fa)
{
	dfn[x]=low[x]=++cnt;s.push(x);fl[x]=1;rg bool first=1;
	for(rll i=0;i<g[x].size();i++)
	{
		rll to=g[x][i].first; if(first&&to==fa) { first=0; continue; }
		if(!dfn[to])
		{
			tarjan(to,x);low[x]=min(low[x],low[to]);
			if(dfn[x]<=low[to])
			{
				bel[x].insert(++tot);num[tot].push_back(x);rll t;
				// 因为点x可能属于多个点双，所以用 vector 存，且不能直接出栈
				do { t=s.top();s.pop();fl[t]=0;bel[t].insert(tot);num[tot].push_back(t); } while(t^to);
			}
		}
		else low[x]=min(low[x],dfn[to]);
	}
}

求边双

边双是一个子图，其内部不存在割边.

求边双其实和求点双差不多，就是栈里点 x 和上面的点构成一个点双.

struct node { ll to,id; };
ll dfn[maxn],low[maxn],cnt,tot;
bool fl[maxn],cut[maxn];
stack<ll> s;
vector<node> g[maxn];
vector<ll> ans[maxn];
inline void tarjan(rll x,rll e)
{
	dfn[x]=low[x]=++cnt; fl[x]=1; s.push(x);
	for(rll i=0;i<g[x].size();i++)
	{
		if(g[x][i].id==(e^1)) continue; rll to=g[x][i].to;
		if(!dfn[to])
			tarjan(to,g[x][i].id),low[x]=min(low[x],low[to]);
		else low[x]=min(low[x],dfn[to]);
	}
	if(dfn[x]==low[x])
	{
		cut[e]=1; tot++; rll t;
		do
		{
			t=s.top();s.pop();ans[tot].push_back(x);
		} while (t^x);
		
	}
}

Tarjan 求 LCA

别以为有这个标题我就会写

这个不常用，一般用倍增或者树剖解决，因此不再描述.

2-SAT

后面会讲.