线段树基础

线段树，是一类维护区间值的数据结构.

它能够实现单点/区间修改加上单点/区间查询，也可以查询区间和、最值等等.

线段树是一棵二叉树，树上的每一个节点表示数列的一个区间.

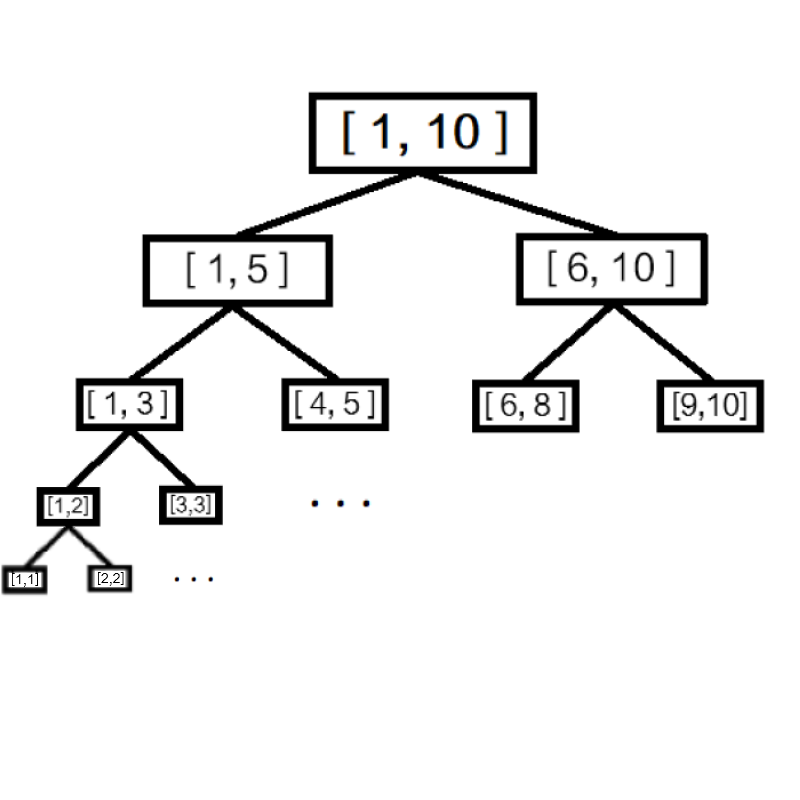
原谅我当初像素没有调好

可以发现它的构成：一个区间 [l , r] 的左子树代表的区间是 [l , ]，右子树代表的区间是 [ + 1 , r].

如何实现？

基本操作

首先，是开数组.

struct tree { ll v,tag; }t[maxn<<2];

空间大小要至少开到4倍以上. 因为一共是 log 层的.

左儿子 lson：

#define ls(x) (x<<1)

右儿子 rson：

#define rs(x) (x<<1|1)

其实就是一个乘 2 和乘 2 加 1 的操作.

然后，就是

建树

inline void build(rll rt,rll l,rll r)
{
    if(l==r) { t[rt].v=a[l]/*原来的数组*/; return; }
    rll mid=(l+r)>>1;build(ls(rt),l,mid);build(rs(rt),mid+1,r);// 递归建树
    pushup(rt);// 向上传递标记
}

在每一次更新的时候，都要上传一次标记，即进行 pushup 操作.

#define pushup(rt) t[rt].sum=(t[ls(rt)].sum+t[rs(rt)].sum),\
                   t[rt].mx=max(t[ls(rt)].mx,t[rs(rt)].mx)

更新

下面展示的是单点修改的操作.

inline void update(rll rt,rll l,rll r,rll pos,rll v)
{
    if(l==r) { t[rt].v=v; /*要修改的值*/ return; }
    rll mid=(l+r)>>1; pushdown(rt,l,r);// 下放之前的标记
    if(pos<=mid) build(ls(rt),l,mid);
    else build(rs(rt),mid+1,r);// 如果要修改的点在左边就去左子树，否则去右子树
    pushup(rt);// 向上传递标记
}

在每一次修改之前，需要把上一次修改操作的标记下放.

因此有一个向下延迟更新的操作 pushdown.

如果只有单点操作，可以不用 pushdown，一遍更新即可. 一般为区间操作或者查询最值时需要 pushdown.

下面展示的是区间修改的操作.

inline void update(rll rt,rll l,rll r,rll x,rll y,rll v)
{   // l、r：当前区间  x、y：所需要修改的区间
    if(x<=l&&r<=y) { t[rt].v=v; /*要修改的值*/ return; } // 在所修改区间内部直接修改并加入tag，用于pushdown
    rll mid=(l+r)>>1; pushdown(rt,l,r);// 下放之前的标记
    if(x<=mid) build(ls(rt),l,mid);
    if(y>mid) build(rs(rt),mid+1,r);// 如果要修改区间的左端点包括在当前区间了，就递归左边；右边同理
    pushup(rt);// 向上传递标记
}

上面展示的是修改为某个值. 如果需要增加某个值，把=改成+=即可.

如何下放标记？

不断把标记向子树传递并且更新权值即可.

inline void pushdown(rll rt,rll l,rll r)// 区间和的下放
{   
    if(t[rt].tag)// 有标记才下放
    {
        rll mid=(l+r)>>1;
        t[ls(rt)].tag+=t[rt].tag; t[rs(rt)].tag+=t[rt].tag;
        t[ls(rt)].v+=t[rt].tag*(mid-l+1); t[rs(rt)].v+=t[rt].tag*(r-mid);
    }
}

查询

查询的话也是很简单的.

也是不断递归子树找到要查询的点或区间，上传这个值.

以下代码均为求和，求最值其实差不多，改成mx或者mn就行了.

下面展示了单点查询的示例：

inline void query(rll rt,rll l,rll r,rll pos)
{   
    if(l==r) return t[rt].v;
    pushdown(rt); rll mid=(l+r)>>1;
    if(pos<=mid) return query(ls(rt),l,mid,pos); else return query(rs(rt),mid+1,r,pos);
}

值得注意的是，查询的时候不需要 pushup，因为并没有修改；但是需要 pushdown，因为修改下传的标记是延迟的，需要传到叶节点.

下面展示了区间查询的示例：

inline void query(rll rt,rll l,rll r,rll x,rll y)
{   
    if(x<=l&&r<=y) return t[rt].v;
    pushdown(rt); rll mid=(l+r)>>1,ans=0;
    if(x<=mid) ans+=query(ls(rt),l,mid,x,y);
    if(y>mid) ans+=query(rs(rt),mid+1,r,x,y);
    return ans;
}

扩展操作

动态开点线段树

在数据较为离散或者需要进行可持久化操作时，常常需要用到动态开点.

这时，lson和rson就不再是乘 2 和乘 2 加 1 了. 需要记录一下每个节点的左右子树的编号. 这里通常在 build() 或 update() 中完成.

下面展示了动态开点线段树的形式与单点修改的更新操作. 注意以当前节点为根，根需要引用.

struct node
{
#define ls(x) t[x].ls
#define rs(x) t[x].rs
	ll v,ls,rs;
}t[maxn<<2];
ll tot;
inline void update(rll& rt,rll l,rll r,rll pos,rll v)
{
	if(!rt) { rt=++tot; ls(rt)=rs(rt)=t[rt].v=0; }
	if(l==r) { t[rt].v=v; return; }
	...(以下内容和正常线段树相同)
}

动态开点可以解决区间为负的情况，注意在 mid 计算时要使其等于 (l+r-1)/2，而不是 (l+r)/2. 否则会 RE.

权值线段树

权值线段树可以用来查询一个数列的第 k 大/小值. 其每个节点存储的是其维护区间内的数出现的次数.

懒得打了，下面粘的几个板子：

单点更新

// 单点更新，某个数字次数+1

void update(int &rt, int l, int r, int pos, int val) {
　　if (!rt) rt = ++tot;
　　if(l == r) {
　　　　tree[rt].cnt++;
　　　　tree[rt].num = val;
　　　　return;
　　}
　　int mid = (l + r) >> 1;
　　if (pos <= mid) update(lson, l, mid, pos, val);
　　else update(rson, mid+1, r, pos, val);
　　tree[rt].cnt = tree[lson].cnt + tree[rson].cnt;
}

查询

// 查询区间[L, R]数字的个数

int query(int rt, int l, int r, int L, int R) {
　　if (!rt) return 0;
　　if (L <= l && r <= R) return tree[rt].cnt;
　　int ans = 0;
　　int mid = (l + r) / 2;
　　if (L <= mid) ans += query(lson, l, r, L, R);
　　if (mid < R) ans += query(rson, l, r, L, R);
　　return ans;
}

// 查询第k大元素

int queryk(int rt, int l, int r, int k) {
　　if (!rt) return -INF;
　　if (l == r) return tree[rt].num;
　　int mid = (l+r)>>1;
　　if (k > tree[rson].cnt) { // 要查的数字在左边
　　　　return queryk(lson, l, mid, k - tree[rson].cnt);
　　} else {
　　　　return queryk(rson, mid+1, r, k);
　　}
}

// 查询比val小/大的个数

// ROOT：树根的编号
// L：值域的最小值
// R：值域的最大值
int lcount(int val) {
　　return query(ROOT, L, R, L, val-1);
}

int rcount(int val) {
　　return query(ROOT, L, R, val+1, R);
}

// 查询val的升序排名

int getrank(int val) {
　　return lcount(val) + 1;
}

// 查询升序中val的前驱/后继

int pre(int val) {
　　int x = lcount(val);
　　return queryk(ROOT, L, R, x);
}
int suc(int val) {
　　int x = getrank(val);
　　return queryk(ROOT, L, R, x+1);
}

线段树合并

就是把两棵线段树合并成一棵，里面保存两棵树中原有的信息.

具体做法：

假设合并线段树 A 和 B，且当前合并到了 pos 位置.

如果 A 树有 pos 位置，B 树没有，返回 A 位置，保存 A 中的数据. 反之如果 B 树有 A 树没有，返回 B.

否则（如果均有 pos 位置）：

如果已经合并到叶子节点了，那么把 B 树中的权加到 A 树上，返回 A 树.

然后递归处理子树，用子树的值更新 A 树的当前节点（即pushup），返回 A树.

实现：

inline ll merge(rll rta,rll rtb,rll l,rll r)
{
	if(!rta) return rtb; if(!rtb) return rta;
	if(l==r) { t[rta].v+=t[rtb].v; return rta; }
	rll mid=(l+r)>>1;
	ls(rta)=merge(ls(rta),ls(rtb),l,mid);
	rs(rta)=merge(rs(rta),rs(rtb),mid+1,r);
	pushup(rta); return rta;
}

线段树可持久化

主席树不是联赛内容，以后再写.

李超线段树

更不是联赛内容，但是既然打了，先给挂上.

它是维护给定线段的数据结构，通过加入一次函数、查找斜率来实现加入与查询线段.

具体维护是把每一个节点打一个标记，作为一条线段.

插入线段时，如果所加入区间无标记，直接更新；若有，则不断递归下传.

具体的下传操作（摘自 oi-wiki）：

原文链接：

传送门

查询的话，就传一个 x 坐标，将所有经过它的的线段进行比较得出最优答案.

下面是模板题（Luogu P4097） 的实现：

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define ld long double
#define rll rg ll
#define maxn 10000001
#define jd 0.0000001// 精度
#define mod 39989
#define moe 1000000000
#define pll pair<ld,ll>
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
struct node
{
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
	ld k,b;
}t[maxn<<2];
ll n,op,cnt,ans,k,_x0,_y0,_x1,_y1;
ll s[maxn<<2];
inline ll cmp(rg ld a,rg ld b) { if(a-b>jd) return 1; if(b-a>jd) return -1; return 0; }// 比较函数，为了防止精度的误差
inline void add(rll _x0,rll _x1,rll _y0,rll _y1)
{
	cnt++; if(_x0==_x1) t[cnt].b=max(_y0,_y1);
	else t[cnt].k=((ld)_y1-_y0)/((ld)_x1-_x0),t[cnt].b=_y0-t[cnt].k*_x0;
}
inline void upd(rll rt,rll l,rll r,rll x)// 下传标记的函数，更新一条线段覆盖到的区间
{
	rll mid=(l+r)>>1,bl,br; if(cmp(t[x].b+t[x].k*mid,t[s[rt]].b+t[s[rt]].k*mid)==1) swap(x,s[rt]);
	bl=cmp(t[x].b+t[x].k*l,t[s[rt]].b+t[s[rt]].k*l),br=cmp(t[x].b+t[x].k*r,t[s[rt]].b+t[s[rt]].k*r);
	if(bl==1||((!bl)&&x<s[rt]/*判断线段编号*/)) upd(ls(rt),l,mid,x);
	if(br==1||((!br)&&x<s[rt])) upd(rs(rt),mid+1,r,x);
}
inline void update(rll rt,rll l,rll r,rll x,rll y,rll v)// 线段拆分，图片里有讲
{
	if(y<l||x>r) return;
	if(x<=l&&r<=y) { upd(rt,l,r,v); return; } rll mid=(l+r)>>1;
	if(x<=mid) update(ls(rt),l,mid,x,y,v); if(y>mid) update(rs(rt),mid+1,r,x,y,v);
}
inline pll max(rg pll a,rg pll b)// pair 比较最大值
{
	if(!~cmp(a.first,b.first)) return b; if(cmp(a.first,b.first)) return a; return a.second<b.second?a:b;
}
inline pll query(rll rt,rll l,rll r,rll pos)// 查询线段
{
	if(pos<l||pos>r) return (pll) { 0,0 };
	rg ld ans=t[s[rt]].b+t[s[rt]].k*pos; if(l==r) return (pll) { ans,s[rt] }; rll mid=(l+r)>>1;
	return max((pll) { ans,s[rt] },max(query(ls(rt),l,mid,pos),query(rs(rt),mid+1,r,pos)));
}
int main()
{
	n=read(); while(n--) switch(op=read())
	{
	case 0: k=(read()+ans-1+mod)%mod+1; write(ans=query(1,1,mod,k).second);putn; break;
	case 1:
		_x0=(read()+ans-1+mod)%mod+1,_y0=(read()+ans-1+moe)%moe+1,_x1=(read()+ans-1+mod)%mod+1,_y1=(read()+ans-1+moe)%moe+1;
		if(_x0>_x1) swap(_x0,_x1),swap(_y0,_y1); add(_x0,_x1,_y0,_y1); update(1,1,mod,_x0,_x1,cnt); break;
	}
	return 0;
}