分治、二分答案

分治算法

分治，顾名思义就是把一个整块的劈成两半，左右分别处理.

没了.

二分答案

二分在 noip 中考查得相对更多一些.

具体就是查询 mid 的值，然后缩小查询区间直至查到需要的点.

rll l=1,r=n,ans;
while(l<=r)
{
	if(check(mid)) ans=mid,l=mid+1;
	else r=mid-1;
}

另一种写法：

rll l=1,r=n,ans;
while(l<r)
{
	if(check(mid)) ans=mid,l=mid;
	else r=mid-1;
}

离散化

STL 中有一个 lower_bound 函数，可以在排好序的序列中查找某个值.

离散化应用了这个函数，将每一个数映射为一个编号，便于以后处理.

实现：

for(rll i=1;i<=n;i++) b[i]=a[i];
sort(b+1,b+n+1); len=unique(b+1,b+n+1)-b-1;
for(rll i=1;i<=n;i++) a[i]=lower_bound(b+1,b+len+1,a[i])-b;

三分法求单峰函数的极值

给出一个 N 次函数，保证在范围 [l, r] 内存在一点 x，使得 [l, x] 上单调增，[x, r] 上单调减. 试求出 x 的值.

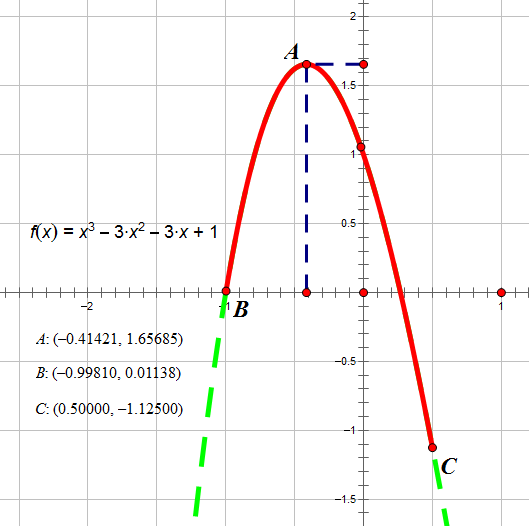
每次取中点值 mid，把它和它右边一点点的函数值比较，这样不断缩小区间直至得到答案.

#include<bits/stdc++.h>
#define ll int
#define ld double
#define rg register
#define rll rg ll
#define jd 0.0000001 // 要求的精度
#define maxn 20001
#define put_ putchar(' ')
#define putn putchar('\n')
using namespace std;
inline ll read()
{
	rll f=0,x=0;rg char ch=getchar();while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();return f?-x:x;
}
inline void write(rll x) { if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10|'0'); }
ll n;
ld l,r,a[maxn];
inline ld chk(rg ld x)
{
	rg ld ans=0; for(rll i=n;i>=0;i--) ans=ans*x+a[i];
	return ans;
}
int main()
{
	n=read();scanf("%lf%lf",&l,&r); for(rll i=n;~i;i--) scanf("%lf",&a[i]);
	while(abs(l-r)>=jd)
	{
		rg ld mid=(l+r)/2;
		if(chk(mid+jd)>chk(mid-jd)) l=mid; else r=mid;
	}
	printf("%.6lf",r);
	return 0;
}