6 . 6

6月6日
考试Day2
使用正睿OI20联赛集训day2题目
这一次考的Just So So...其实也没有特别突出.
因为是子任务绑定，不对就没分了，所以大家分数都很低.

#	用户名	交通	冒泡排序	矩阵	花瓶	总分
1	1Liu	60 03:02:01	0 03:30:26	100 02:25:32	50 02:46:36	210 03:30:26

T1

交通
题面

题解:

假设一个点的两条出边为 \(i,j\)，我们新建一个图给 \(i,j\) 连边.如果一个点的两条入边为 \(i,j\)，我们也给 \(i,j\) 连边.

不难发现新图上每个点度数恰好为二，并且只有偶环.我们的要求事实上就是在新图上选 \(n\) 个不相邻的点，于是答案显然是 \(2^{\texttt{环数}}\)，直接并查集即可.
当然，我在做这个题的时候用tarjan缩了一个点，使用并查集当然更简单.

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 1000001
#define mod 998244353
#define rll rg ll
using namespace std;
ll n;
vector<ll> g[maxn][2],e[maxn];
ll dfn[maxn],low[maxn],cnt;
ll tot;
bool vis[maxn];
stack<ll> s;
inline void tarjan(ll x)
{
	dfn[x]=low[x]=++cnt;
	vis[x]=1;s.push(x);
	for(rll i=0;i<e[x].size();i++)
	{
		if(!dfn[e[x][i]])
			tarjan(e[x][i]),
			low[x]=min(low[x],low[e[x][i]]);
		else if(vis[e[x][i]])
			low[x]=min(low[x],dfn[e[x][i]]);
	}
	if(dfn[x]==low[x])
	{
		rll tmp;tot=(tot+1)%mod;
		do { tmp=s.top();vis[tmp]=0;s.pop(); } while(tmp!=x);
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin>>n;
	for(rll i=1,u,v;i<=(n<<1);i++)
	{
		cin>>u>>v;
		g[u][0].push_back(i);
		g[v][1].push_back(i);
	}
	for(rll i=1;i<=n;i++)
		for(rll j=0;j<=1;j++)
			e[g[i][j][0]].push_back(g[i][j][1]),
			e[g[i][j][1]].push_back(g[i][j][0]);
	for(rll i=1;i<=(n<<1);i++) if(!dfn[i]) tarjan(i);
	cout<<(1<<tot)%mod;
	return 0;
}

T2

冒泡排序
题面

题解：

首先若存在 \(a_i=i\)，显然无解.
若 \(a_i>i\)，则我们需要把这个数字从 \(i\) 位置向右挪到 \(a_i\) 位置上.于是就会发现相邻位置的交换顺序有一些限制，限制形如某对相邻的交换必须在它旁边的相邻对交换之前/之后.
\(a_i<i\) 就是把 \(i\) 位置向左挪到 \(a_i\) 的位置上，限制也类似.
于是问题就变成了有若干个形如 \(b_i>b_{i-1}\) 或 \(b_i<b_{i-1}\) 的限制，问满足要求的排列 \(b\) 有多少个.
直接 \(O(n^2)\) dp 即可，当然可以容斥+分治 FFT 优化成 \(O(n\log^2n)\)，但由于这是 NOIP 模拟赛就不说了.

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 5001
#define mod 1000000007
#define rll rg ll
using namespace std;
ll n,cnt,ans;
ll a[maxn];
ll dp[2][maxn];
bool u[maxn];
short fl[maxn];
int main()
{
	ios::sync_with_stdio(0);
	cin>>n;
	for(rll i=1;i<=n;i++)
	{
		cin>>a[i];a[i]++;
		if(a[i]==i)
		{//手模一下，如果有数字就在本来位置的肯定要比n-2要不同.比如n-2是奇数，那么最少移动次数一定是偶数，是无法达成的.
			cout<<0;
			return 0;
		}
	}
	for(rll i=1;i<=n;i++)
		for(rll j=i+1;j<=n;j++)
			if(a[i]>a[j]) cnt++;
	for(rll i=1;i<=n;i++)
        for(rll j=i+1;j<=n;j++)
            if(a[j]==i)
            {
                for(rll k=i;k<j;k++)
                {
                    if(u[k])
                    {
                        cout<<0;
                        return 0;
                    }
                    u[k]=1;
                    fl[k]=1;
                }
                if(i>1) fl[i-1]=-1;
                break;
            }
	dp[0][1]=1;
	for(rll i=2;i<n;i++)
	{
		memset(dp[1],0,sizeof(dp[1]));
		if(fl[i-1]==-1)
			for(rll j=1;j<=i;j++)
				dp[1][j]=dp[1][j-1],
				dp[1][j]=(dp[1][j]+dp[0][j-1])%mod;
		else
			for(rll j=i;j;j--)
				dp[1][j]=dp[1][j+1],
				dp[1][j]=(dp[1][j]+dp[0][j])%mod;
		swap(dp[0],dp[1]);
	}
	for(rll i=1;i<=n;i++)
		ans=(ans+dp[0][i])%mod;
	cout<<ans;
	return 0;
}

T3

矩阵

题目描述

qjd 有一个 \(n×m\) 的矩阵，矩阵里每个元素都是个整数（可能是负数）.qjd 觉得这个矩阵非常杂乱，因此他让你
来清理这个矩阵.
具体的，你可以执行以下三种操作若干次，使得整个矩阵里所有元素都变成 \(0\) .

把某一行里的元素全部加上整数 \(k\) （可以为负）.
把某一列里的元素全部加上整数 \(k\) （可以为负）.
把某一主对角线里的元素全部加上整数 \(k\) （可以为负）.

这里主对角线指行编号和列编号之差为定值的一些格子.

例如 \(3×4\) 的矩阵里，\((1,1),(2,2),(3,3)\)是一条主对角线，\((1,2),(2,3),(3,4)\)也是一条，\((2,1),(3,2)\)也是一条
（特别的，\((3,3)\)也是一条主对角线）.

你可以执行这些操作总共不超过 \(6000\) 次或者报告无解.

输入格式

第一行两个正整数 \(n,m\) .
接下来 \(n\) 行每行 \(m\) 个整数表示矩阵.

输出格式

第一行一个整数 \(K\) 表示操作次数.输出 \(K=-1\) 的话表示你认为输入的矩阵无解.
若 \(K>0\)，接下来 \(K\) 行每行格式如下：
若执行了操作 \(1\)，输出一行 \(1\text{ }x\text{ }k\) ，其中 \(x(1 \le x \le n)\) 表示行的编号.
若执行了操作 \(2\)，输出一行 \(2\text{ }x\text{ }k\) ，其中 \(x(1 \le x \le m)\) 表示列的编号.
若执行了操作 \(3\)，输出一行 \(3\text{ }x\text{ }k\) ，其中 \(x(1-n \le x \le m-1)\) 表示列编号减行编号（根据主对角线的定义，这是个常数，可以为负）.
上面的 \(k\) 都表示操作的参数（即格子加上的数字）.你需要保证 \(|k| \le 10^{18}\).

样例

样例输入 1

2 2
1 2
3 4

样例输出 1

样例输入 2

样例输出 2

-1

数据范围与提示

对于所有数据，保证 \(n,m\ge2,n,m\le1000\)，矩阵中的数的绝对值不超过 \(10^9\).
\(subtask1(20pts) : n=2\)
\(subtask2(20pts) :\) 保证若有解则不用 3 操作就可以把矩阵变成全 \(0\).
\(subtask3(30pts) : n,m\le100\)
\(subtask4(30pts) :\) 无特殊限制.

题解：

题解：
这个题的一个极有意思的地方在于：我们只需要把前两行与前两列变成0.
为什么呢？
在这里，假设构造一个\(3×3\)的矩阵，

a	b	c
d	e	f
g	h	i

可以发现：
\(a-b-d\)与\(i-h-f\)的差是一个定值.
即：

\[a-b-d=i-h-f+k , k\in \Z \]

证明：
考虑在每一行加上一个数 \(p\) ，
如果在第一行加，那么有：

\[(a+p)-(b+p)-d=i-h-f+k, \]

化简得：

\[a-b-d=i-h-f+k \]

如果在第二行加，那么有：

\[a-b-(d+p)=i-h-(f+p)+k, \]

化简得：

\[a-b-d=i-h-f+k \]

发现和原式相同.

因此，只需要把前两行和前两列变成 \(0\) 即可，如果此时还不能把整个矩阵归零那么必然无解.证明就考
虑任意一个 \(3×3\) 的矩阵，\(a_{1,1}-a_{1,2}-a_{2,1}+a_{2,3}+a_{3,2}-a_{3,3}\) 的值在这些操作下永远不变.
于是这样的构造是很容易的，\(4000\) 次操作就足够了.

//一个有趣的性质：
//如果前2行和前2列均为0，那么该矩阵就全部为0
//否则无解.
#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 1001
#define mod 1000000007
#define rll rg ll
using namespace std;
struct node
{
	ll id,v;
}aa[maxn<<3],bb[maxn<<3],cc[maxn<<3];
ll cnta,cntb,cntc;
ll n,m,p,ans;
ll d[maxn][maxn];
bool fl;
ll a[maxn],b[maxn],c[maxn<<3];
int main()
{
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(rll i=1;i<=n;i++)
		for(rll j=1;j<=m;j++)
			cin>>d[i][j];
	a[1]=d[2][2]-d[1][1];
	c[n]=-d[2][2];
	//分别将前2行和前2列暴力修改为0
	for(rll i=2;i<=n;i++)//行
	{
		c[n-i+1]=-(d[i][1]+a[i]);
		a[i+1]=-(d[i+1][2]+c[n-i+1]);
	}
	for(rll i=2;i<=m;i++)//列
	{
		c[n+i-1]=-(d[1][i]+a[1]+b[i]);
		b[i+1]=-(d[2][i+1]+c[n+i-1]);
	}
	for(rll i=1;i<=n;i++)//每个位置模拟一遍判断有无解
		for(rll j=1;j<=m;j++)
			if(d[i][j]+a[i]+b[j]+c[n-(i-j)])
				fl=1;
	if(fl) cout<<-1;
	else
	{
		for(rll i=1;i<=n;i++) if(a[i]) aa[++cnta]={ i,a[i] };
		for(rll i=1;i<=m;i++) if(b[i]) bb[++cntb]={ i,b[i] };
		for(rll i=1;i<n+m;i++) if(c[i]) cc[++cntc]={ i-n,c[i] };
		cout<<cnta+cntb+cntc<<endl;
		for(rll i=1;i<=cnta;i++) cout<<"1 "<<aa[i].id<<' '<<aa[i].v<<endl;
		for(rll i=1;i<=cntb;i++) cout<<"2 "<<bb[i].id<<' '<<bb[i].v<<endl;
		for(rll i=1;i<=cntc;i++) cout<<"3 "<<cc[i].id<<' '<<cc[i].v<<endl;
	}
	return 0;
}

T4

花瓶

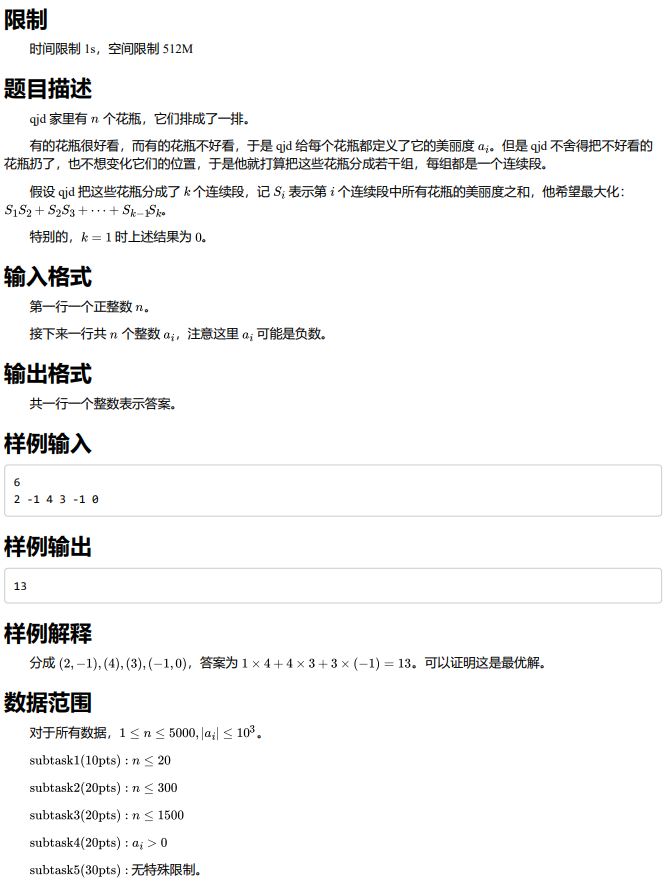
题解：
简单的斜率优化.

考虑 \(f_{i,j}\) 表示当前 dp 到了 \(i\)，上一个区间右端点为 \(j\) 时的最优答案.则显然有：

\[f_{i,j} = \max_{0≤k<j}f_{j,k}+(s_i−s_j )(s_j−s_k) \]

显然是个斜率优化的形式，扔掉只和有关的常数项，则可以写成：

\[f_{i,j}=p+\max_{0≤k<j}f_{j,k}−t⋅s_k \]

若对于 \(s_a<s_b\) 有 \(f_{j,a}−t⋅s_a<f_{j,b}−t⋅s_b\) ，那么显然：

\[\frac{f_{j,a}−f_{j,b}}{s_a−s_b}>t \]

于是我们枚举 \(j\)，按照 \(s\) 排序后暴力维护出一个斜率递减的上凸壳.注意到 \(t=s_i−s_j\)，我们再按照 \(s_i\) 从大到小枚举 \(i\)，就可以贪心地从凸包前面删点了.
于是总复杂度 \(O(n^2)\).

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 5001
#define rll rg ll
using namespace std;
ll id[maxn],sum[maxn];
inline bool cmp(ll a,ll b)
{
	return sum[a]<sum[b];
}
ll n,ans;
ll a[maxn];
ll dp[maxn][maxn];
deque<ll> q;
int main()
{
	freopen("d.in","r",stdin);
	freopen("d.out","w",stdout);
	ios::sync_with_stdio(0);
	memset(dp,-0x3f,sizeof(dp));
	cin>>n;
	for(rll i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i],id[i]=i;
	sort(id+0,id+n+1,cmp);
	for(rll i=0;i<=n;i++) dp[i][0]=0;
	for(rll i=1;i<=n;i++)
	{
		while(!q.empty()) q.pop_back();
		for(rll j=0;j<=n;j++)
			if(id[j]<i)
			{
				while(q.size()>=2&&
					(dp[i][q.back()]-dp[i][q[q.size()-2]])*(sum[id[j]]-sum[q[q.size()-2]])<=(dp[i][id[j]]-dp[i][q[q.size()-2]])*(sum[q.back()]-sum[q[q.size()-2]]))
					q.pop_back();
				q.push_back(id[j]);
			}
		for(rll j=n;j>=0;j--)
			if(id[j]>i)
			{
				while(q.size()>=2&&
					(sum[id[j]]-sum[i])*(sum[q[1]]-sum[q.front()])<=(dp[i][q[1]]-dp[i][q.front()]))
					q.pop_front();
				dp[id[j]][i]=max(dp[id[j]][i],dp[i][q.front()]+(sum[id[j]]-sum[i])*(sum[i]-sum[q.front()]));
			}
	}
	for(rll i=0;i<n;i++)
		ans=max(ans,dp[n][i]);
	cout<<ans;
	return 0;
}

posted @ 2022-06-07 16:52 1Liu 阅读(182) 评论(0) 收藏举报

刷新页面返回顶部

1Liu's Blog

进学致和，行方思远.

6 . 6

T1

T2

T3

T4

公告