6 . 5

6月5日

考试Day1
用的是正睿2021 CSP 7 day2的题.

这一次考得并不理想，

#	用户名	2A	2B	2C	2D	总分
23	1Liu	70 00:17:14	100 00:37:05	14 01:50:25	20 03:50:57	204 03:50:57

看着这个名次确实是有一些愧疚.

呃呃呃……

废话少说，进入正题：

T1

IP地址

一道水题，从前往后扫一遍字符串就可以了.

我当时没有考虑0的情况，痛失30分啊啊......

//代码丑了，凑合看看吧.
#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 10001
#define rll rg ll
using namespace std;
ll len;
char s[maxn];
ll a[5],cnt;
bool fl,hf;
int main()
{
	ios::sync_with_stdio(0);
	cin>>s+1;
	len=strlen(s+1);
	for(rll i=1;i<=len;i++)
	{
		if((!fl)&&(s[i]<'0'||s[i]>'9'))
			hf=1;
		else if(!fl)
		{
			a[++cnt]=s[i]-'0';
			if(s[i]=='0'&&s[i+1]>'0'&&s[i+1]<='9')
				hf=1;
			if(s[i+1]=='0') hf=1;
			while(s[i+1]>='0'&&s[i+1]<='9')
				a[cnt]=a[cnt]*10+s[++i]-'0';
			if(a[cnt]>255)
				hf=1,a[cnt]=255;
			fl=1;
		}
		else
		{
			if(cnt==4) hf=1;
			if(s[i]!='.') hf=1;
			fl=0;
		}
	}
	cout<<(hf?"NO":"YES")<<endl;
	if(hf) cout<<a[1]<<'.'<<a[2]<<'.'<<a[3]<<'.'<<a[4];
	return 0;
}

T2

字符串

简单的KMP，利用贪心原则把AP先找到并删除，再重新组建字符串，找到PP并删除.

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 10001
#define rll rg ll
using namespace std;
ll len,lent=2;
char s[maxn],s1[maxn];
ll cnt;
bool fl,hf;
char t[2][3]={ {0,'A','P'},{0,'P','P'} };
ll kmp[maxn],kmp2[maxn];
stack<ll> st;
inline void KMP(ll len,char* t)
{
	rll j=0;
	for(rll i=2;i<=len;i++)
	{
		while(j&&t[i]!=t[j+1]) j=kmp[j];
		if(t[i]==t[j+1]) j++;
		kmp[i]=j;
	}
}
inline void kmp_two(ll lena,char* s,ll lenb,char* t)
{
	rll j=0;
	for(rll i=1;i<=lena;i++)
	{
		while(j&&s[i]!=t[j+1]) j=kmp[j];
		if(s[i]==t[j+1]) j++;
		kmp2[i]=j;
		st.push(i);
		if(j==lenb)
		{
			while(j--) st.pop();
			if(!st.empty()) j=kmp2[st.top()];
			else j=0;
		}
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin>>s+1;
	len=strlen(s+1);
	KMP(lent,t[0]);
	kmp_two(len,s,lent,t[0]);
	len=st.size();
	while(!st.empty())
		s1[len-(cnt++)]=s[st.top()],st.pop();
	memset(kmp,0,sizeof(kmp));
	memset(kmp2,0,sizeof(kmp2));
	KMP(lent,t[1]);
	kmp_two(len,s1,lent,t[1]);
	cout<<st.size();
	return 0;
}

T3

继承类

现在发明了一种类似于 C++ 的面向对象编程语言中的类声明.

每个类声明的格式为 "K : \(P_1\ P_2\ \dots\ P_K\);"

其中 \(K\) 是要声明的新类的名称，\(P_1 、P_2 、\dots 、P_k\) 类 \(K\) 继承的类的名称.

例如，"shape : ;" 是不继承任何其他类的类 “shape” 的声明，而 “square : shape rectangle;” 是继承类 “shape” 和 “rectangle” 的类 “square” 的声明.

如果类 \(K_1\) 继承类 \(K_2\) ，类 \(K_2\) 继承类 \(K_3\) ，依此类推，直到类 \(K_{m−1}\) 继承类 \(K_m\) ，那么我们说所有类 \(K_1,K_2,\dots,K_{m−1}\) 派生自类 \(K_m\) .

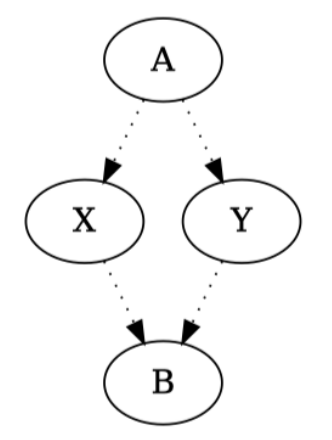
编程语言的规则禁止循环定义，因此不允许从自身派生一个类.换句话说，类层次结构形成了一个有向无环图.此外，不允许在类层次结构中出现所谓的菱形.一个菱形由四个不同的类 \(A、B、X、Y\) 组成，而且它满足（如下图所示）：

类 \(X\) 和 \(Y\) 派生自 \(A\).
类 \(B\) 派生自 \(X\) 和 \(Y\).
类 \(X\) 不是从 \(Y\) 派生的，类 \(Y\) 也不是从 \(X\) 派生的.

现在你会获得一系列要按顺序处理的类声明，并确定每个类声明是否是正确声明.

正确声明的类被添加到层次结构中，而错误的类被丢弃.声明 “K : \(P_1\ P_2\ \dots\ P_K\);” 如果满足以下条件，则认为是正确声明：

类 \(K\) 尚未声明.
所有类别 \(P_1,P_2,\dots,P_k\) 之前已经声明过.请注意，此条件可确保类永远不会从其自身派生，或者类层次结构中不能存在循环.
通过添加继承了 \(P_1,P_2,\dots,P_k\) 的类 \(K\) 以后，类层次结构保持有序，即没有形成任何菱形.
现在需要你分别处理上述声明并确定每个声明的正确性.

input

10
shape : ;
rectangle : shape ;
circle : shape ;
circle : ;
square : shape rectangle ;
runnable : object ;
object : ;
runnable : object shape ;
thread : runnable thread ;
applet : square thread ;

output

ok
ok
ok
greska
ok
greska
ok
ok
ok
greska

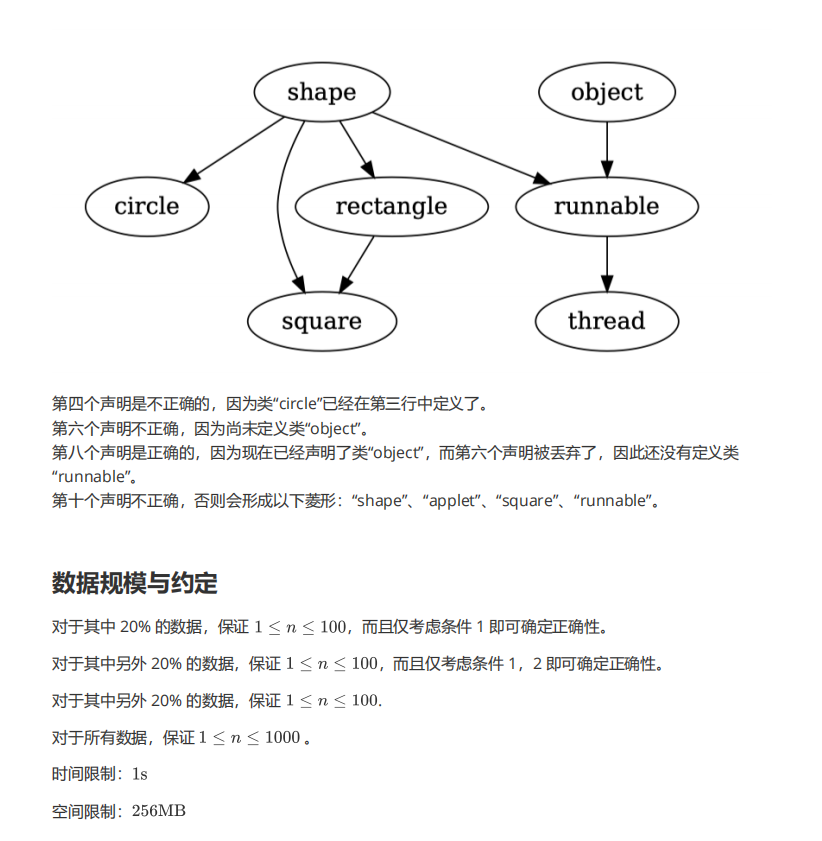
这里的“菱形”指所有的 \(P_i\) 不能为旁系亲属，要么是严格的祖孙关系，要么毫无关系.
则有如果当前的类定义合法，那么所有的 \(P_i\) 的旁系亲属都是当前 \(K\) 的旁系亲属.

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 1001
#define rll rg ll
using namespace std;
map<string,ll> mp;
bitset<maxn> a[maxn],b[maxn],tmp;
ll n,cnt,tot,f[maxn];
char s[maxn],t[maxn];
bool fl;
int main()
{
	ios::sync_with_stdio(0);
	cin>>n;
	for(rll i=1;i<=n;i++)
	{
		fl=0;cnt=0;
		cin>>s+1;
		cin>>t+1>>t+1;
		while(t[1]!=';')
		{
			if(!mp[t+1]) fl=1;
			f[++cnt]=mp[t+1];
			cin>>t+1;
		}
		tmp.reset();
		rg bool flag=0;
		for(rll i=1;i<=cnt;i++)
			tmp[f[i]]=1;
		for(rll i=1;i<=cnt;i++)
			if((tmp&b[f[i]]).any())
				flag=1;
		if(flag) fl=1;
		if(fl||mp[s+1])
		{
			cout<<"greska"<<endl;
			continue;
		}
		mp[s+1]=++tot;
		a[tot][tot]=1;
		for(rll j=1;j<=cnt;j++)
			a[tot]|=a[f[j]];
		for(rll j=1;j<tot;j++)
			if((!a[tot][j])&&(a[j]&a[tot]).any())
				b[tot][j]=1;
		cout<<"ok"<<endl;
	}
	return 0;
}

T4

子图

Cuber QQ 的研究兴趣是在图 \(G=(V(G),E(G))\) 中找到最好的 \(k\)-degree 子图.

子图 \(S\) 是 \(G\) 的 \(k\)-degree 子图需要满足以下要求：

每个顶点 \(v(v\in S)\) 在 \(S\) 中至少有 \(k\) 度；
\(S\) 是连通的 ;
\(S\) 是极大的，即 \(S\) 的任何超图都不是 \(k\)-degree 子图，除了 \(S\) 本身.

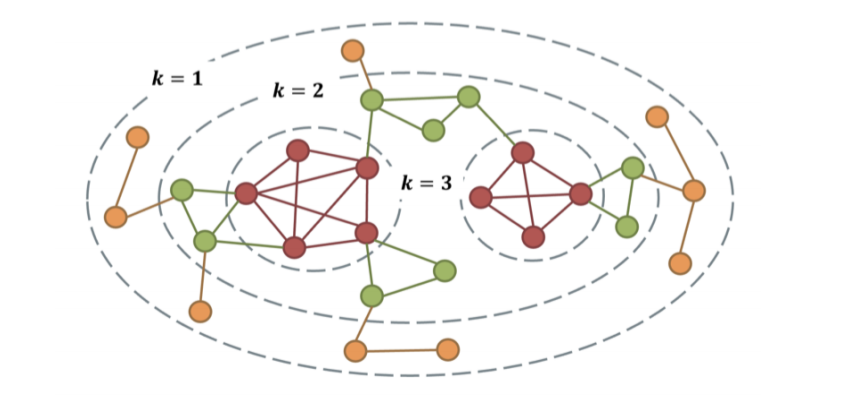
然后 Cuber QQ 定义子图 \(S\) 的分数.在定义分数之前，他首先定义：

\(n(S)\)：子图 \(S\) 中的顶点数，即 \(n(S)=|V(S)|\)；
\(m(S)\)：子图 \(S\) 的边数，即 \(m(S)=|E(S)|\)；
\(b(S)\)：子图 \(S\) 中的边界边数，\(b(S)=|{(u,v)|(u,v)∈E(G),u∈V(S),v∉V(S),v∈V(G)}|\);
他定义一个子图的分数为 \(score(S)=M\cdot m(S)−N\cdot n(S)+B\cdot b(S)\)，其中 \(M,N,B\) 是给定的常数.

子图的分数越高，Cuber QQ 认为它越好.你需要在图 \(G\) 中找到最好的 \(k\)-degree 子图.如果有许多 \(k\)-degree 子图的分数相同，则应最大化 \(k\).

首先可以发现，如果不考虑连通性问题，\((k + 1)-\text{degree}\) 一定是 \(k-\text{degree}\) 的子图
如果一个点属于 \((k + 1)-\text{degree}\) 而不属于 \(k-\text{degree}\)，我们可以把这个点标记为 \(k + 1\)
所以我们可以考虑找到 k 最大的 \(k-\text{degree}\)，然后考虑不断的拓展这个子图，去得到 \(k\) 比较小
的 \(k-\text{degree}\)
显然每一次加入一批相同标记的点，可以拓展得到 \(k\) 减小的 \(k-\text{degree}\)
假设我们已经知道了当前图的 \(score\) ，我们考虑新增点/边会带来的 \(score\) 变化
我们首先给所有的节点一个 \(rank\)

\(rank(v) > rank(u)\) 当且仅当
– \(v\) 的标记 \(>\) \(u\) 的标记
– \(v\) 的标记 \(=\) \(u\) 的标记且 \(v > u\)
这个部分可以用 \(\text{bin-sort}\) 完成

我们可以根据边两边点的 \(rank\) 对边分类，用 \(E(v, >)\) 表示 \(v\) 的边中另一个端点比 \(v\) \(rank\) 大
的边，其余的表示以此类推
于是，考虑新增一批点（标记相同的点）：对于每一个新加入的点 \(u\)：

\(∆n = 1\)
\(∆m = |E(u, >)| + \frac{1}{2}|E(u, =)|\)
\(∆b = |E(u, <)| − |E(u, >)|\)

于是从标记大的点到小的点依次加入计算 \(score\)，得到最大 \(score\) 的 \(k\) 即可
因为不断加入点，可能使得本来不连通的两个子图联通起来，这部分可以用并查集维护
时间复杂度 \(O(m + n)\)

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 1000001
#define rll rg ll
using namespace std;
inline ll Read()
{
#define read Read()
	rll f=0,x=0;rg char c=getchar();
	while(c<'0'||c>'9') f|=c=='-',c=getchar();
	while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
	return f?-x:x;
}
struct node
{
	ll id,n,m,b;
}a[maxn];
ll n,m,cnt,num;
ll f[maxn];
ll du[maxn];
queue<ll> q;
ll M,N,B,k,ans=-0x7fffffffffffffff;
vector<ll> g[maxn];
vector<ll> sz[maxn];
inline ll find(ll x)
{
	if(x!=f[x]) f[x]=find(f[x]);
	return f[x];
}
int main()
{
	n=read;m=read;
	M=read;N=read;B=read;
	for(rll i=1,u,v;i<=m;i++)
	{
		u=read;v=read;
		g[u].push_back(v);
		g[v].push_back(u);
		du[u]++;du[v]++;
	}
	for(rll i=1;i<=n;i++) f[i]=i;
	for(rll i=1;i<=n;i++)
	{
		a[i].n=1;
		a[i].b=du[i];
	}
	for(rll i=1;i<=n;i++)
		if(!du[i]) cnt++;
	for(rll i=1;i<=n;i++)
	{
		for(rll j=1;j<=n;j++)
			if(du[j]==i) q.push(j);
		while(!q.empty())
		{
			rll tmp=q.front();q.pop();
			sz[i].push_back(tmp);
			a[tmp].id=i;
			cnt++;
			for(rll k=0;k<g[tmp].size();k++)
			{
				du[g[tmp][k]]--;
				if(du[g[tmp][k]]==i)
					q.push(g[tmp][k]);
			}
		}
		if(cnt==n)
		{
			num=i;
			break;
		}
	}
	for(rll i=num;i;i--)
	{
		for(rll j=0;j<sz[i].size();j++)
		{
			for(rll k=0;k<g[sz[i][j]].size();k++)
			{
				rll to=g[sz[i][j]][k];
				if(i<a[to].id||(i==a[to].id&&sz[i][j]<to))
				{
					rll x=find(sz[i][j]),y=find(to);
					if(x!=y)
					{
						f[y]=x;
						a[x].m+=a[y].m+1;
						a[x].n+=a[y].n;
						a[x].b+=a[y].b-2;
					}
					else
						a[x].m++,
						a[x].b+=-2;
				}
			}
		}
		for(rll j=0;j<sz[i].size();j++)
		{
			rll tmp=find(sz[i][j]);
			if(ans<a[tmp].m*M-a[tmp].n*N+a[tmp].b*B)
			{
				ans=a[tmp].m*M-a[tmp].n*N+a[tmp].b*B;
				k=i;
			}
		}
	}
	printf("%lld %lld",k,ans);
	return 0;
}

posted @ 2022-06-07 16:50 1Liu 阅读(206) 评论(0) 收藏举报

刷新页面返回顶部

1Liu's Blog

进学致和，行方思远.

6 . 5

6月5日

T1

T2

T3

T4

公告