gym923B
Even though he isn't a student of computer science, Por Costel the pig has started to study Graph Theory. Today he's learning about Bellman-Ford, an algorithm that calculates the minimum cost path from a source node (for instance, node 1) to all the other nodes in a directed graph with weighted edges. Por Costel, utilizing his scarce programming knowledge has managed to scramble the following code in C++, a variation of the Bellman-Ford algorithm:

You can notice a lot of deficiencies in the above code. In addition to its rudimentary documentation, we can see that Por Costel has stored this graph as an array of edges (the array  ). An edge is stored as the triplet
). An edge is stored as the triplet 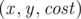 signifying an edge that spans from
signifying an edge that spans from  to
to 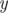 and has weight
and has weight 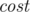 . But even worse is the fact that the algorithm is SLOW!
. But even worse is the fact that the algorithm is SLOW!
As we want our hooved friend to walk away with a good impression about computer science, we want his code to execute as FAST as possible. In order to do so, we can modify the order of edges in the array  so that the while loop executes a small number of times.
so that the while loop executes a small number of times.
Given a directed graph of 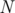 nodes and
nodes and  edges, you are asked to produce an ordering of the edges such that the Bellman-Ford algorithm written by Por Costel should finish after at most two iterations of the while loop(that is, the program should enter the while loop at most twice).
edges, you are asked to produce an ordering of the edges such that the Bellman-Ford algorithm written by Por Costel should finish after at most two iterations of the while loop(that is, the program should enter the while loop at most twice).
The first line of the file algoritm.in will contain an integer 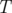
 , the number of test cases.
, the number of test cases.
Each of the 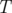 test cases has the following format: on the first line, there are two numbers
test cases has the following format: on the first line, there are two numbers 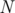 and
and  (
(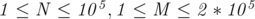 ), the number of nodes and the number of edges in the graph respectively.
), the number of nodes and the number of edges in the graph respectively.
The next  lines describe the edges, each containing three integers
lines describe the edges, each containing three integers 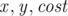 signifying there is an edge from node
signifying there is an edge from node  to node
to node 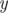 with weight
with weight 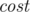 (
(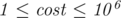 )
)
It is guaranteed that node 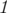 has at least one outgoing edge.
has at least one outgoing edge.
The graph may contain self loops and/or multiple edges.
The output file algoritm.out should contain 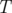 lines representing the answers to each test case.
lines representing the answers to each test case.
For each test case you should output a permutation of numbers from 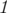 to
to  , representing the order of the edges you want in Por Costel's array of edges
, representing the order of the edges you want in Por Costel's array of edges  .
.
The edges are considered indexed by the order in which they are given in the input (the  -th edge read is the edge with index
-th edge read is the edge with index  ).
).
If there are multiple solutions, you are allowed to print any of them.
1
4 4
1 2 1
3 4 2
2 3 3
1 3 1
1 4 2 3
dijiestra存访问路径
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
const int inf=1<<29;
typedef pair<int,int> PII;
struct edge
{
int v,val,i;
};
priority_queue<PII,vector<PII>,greater<PII> >q;
vector<edge>graph[100100];
vector<int>num;
int n,m,u,v,val,T;
int d[100100],used[200100],use[200100];
void dijiestra()
{
memset(used,0,sizeof(used));
q.push(PII(0,1));
while(!q.empty())
{
PII x=q.top();q.pop();
int u=x.second;
if(used[u]) continue;
used[u]=1;
for(int i=0;i<graph[u].size();i++)
{
edge x=graph[u][i];
int v=x.v,val=x.val;
if(d[v]>d[u]+val){d[v]=d[u]+val;num.push_back(x.i);use[x.i]=1;q.push(PII(d[v],v));}
}
}
// for(int i=1;i<=n;i++) cout<<d[i]<<" ";
// cout<<endl;
for(int i=0;i<num.size();i++) printf("%d ",num[i]);
for(int i=1;i<=m;i++) if(!use[i]) printf("%d ",i);
cout<<endl;
}
int main()
{
freopen("algoritm.in","r",stdin);
freopen("algoritm.out","w",stdout);
cin>>T;
while(T--)
{
cin>>n>>m;
for(int i=2;i<=n;i++) d[i]=inf;
memset(use,0,sizeof(use));
num.clear();
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&val);
edge e;
e.v=v,e.val=val,e.i=i;
graph[u].push_back(e);
}
dijiestra();
for(int i=1;i<=n;i++)
graph[i].clear();
}
fclose(stdin);
fclose(stdout);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号