题解 P3647 [APIO2014]连珠线

题解

这里提供一种与其他题解不太相同的做法。

首先最后的树中只可能有这两种蓝线。

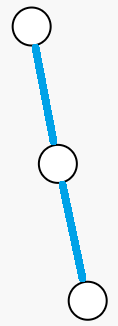
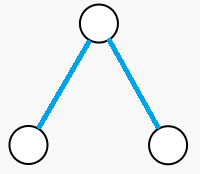
其次如果把一个为蓝线端点的点当作根，那就只有第一种情况。

因此一个做法是，枚举每个点为根时，根据第一种情况进行树形 dp。

具体的，设 \(w_{i,j}\) 表示 \(i,j\) 之间连线的权值，\(f_{i,0/1}\) 表示 \(1\) 为根时 \(i\) 的子树中，\(i\) 是/不是蓝线中点时答案的最大值。

\(f_{i,0}=\underset{v\in son_i}{\sum}\max(f_{v,0},f_{v,1}+w_{i,v})\)

\(f_{i,1}=f_{i,0}+\underset{v\in son_i}{\max}(f_{v,1}+w_{i,v}-f_{v,0})\)

接下来进行换根操作。

具体的，设 \(j\) 为 \(i\) 的某个儿子，\(dp_{i,0/1,j}\) 表示 \(1\) 为根时 \(i\) 的子树中，不考虑 \(j\) 的子树，\(i\) 是/不是蓝线中点时答案的最大值，\(g_{i,0/1}\) 表示 \(1\) 为根时整棵树中，不考虑 \(i\) 的子树，\(i\) 是/不是蓝线中点时答案的最大值。

答案即为 \(f_{i,0}+g_{i,0}\) 的最大值。

\(dp_{i,0,j}=\underset{v\in son_i,v\neq j}{\sum}\max(f_{v,0},f_{v,1}+w_{i,v})\)

\(dp_{i,1,j}=dp_{i,0,j}+\underset{v\in son_i,v\neq j}{\max}(f_{v,1}+w_{i,v}-f_{v,0})\)

\(g_{j,0}=\max(g_{i,0}+dp_{i,0,j},\max(g_{i,1}+dp_{i,0,j},g_{i,0}+dp_{i,1,j})+w_{i,j}\)

\(g_{j,1}=g_{i,0}+dp_{i,0,j}+w_{i,j}\)

具体实现用 vector 和最大次大值维护一下即可 \(O(1)\) 换根。

Code

#include<cstdio>
#include<vector>
#define inf 0x3f3f3f3f
using namespace std;
int n,edge_t=0,ans=0;
int la[200002]={},mx[200002],sec[200002];
int f[200002][2],g[200002][2];
vector<int> dp[200002][2];
struct aaa
{
	int to,nx,val;
}edge[400002];
inline int max(int x,int y)
{
	return x>y? x:y;
}
inline void add_edge(int x,int y,int z)
{
	edge[++edge_t]=(aaa){y,la[x],z},la[x]=edge_t;
	edge[++edge_t]=(aaa){x,la[y],z},la[y]=edge_t;
}
inline void dfs(int x,int fa)
{
	mx[x]=sec[x]=-inf,f[x][0]=0;
	for(int i=la[x],v,w,w1;i;i=edge[i].nx)
		if((v=edge[i].to)!=fa)
		{
			dp[x][0].push_back(0),dp[x][1].push_back(0),dfs(v,x),f[x][0]+=(w1=max(f[v][0],f[v][1]+edge[i].val));
			if((w=f[v][0]+edge[i].val-w1)>mx[x])sec[x]=mx[x],mx[x]=w;else if(w>sec[x])sec[x]=w;
		}
	f[x][1]=f[x][0]+mx[x];
}
inline void dfs1(int x,int fa)
{
	int t=0;
	for(int i=la[x],v;i;i=edge[i].nx)
		if((v=edge[i].to)!=fa)
		{
			dp[x][0][t]=dp[x][1][t]=f[x][0]-max(f[v][0],f[v][1]+edge[i].val),dfs1(v,x);
			if(mx[x]==f[v][0]+edge[i].val-max(f[v][0],f[v][1]+edge[i].val))dp[x][1][t]+=sec[x];else dp[x][1][t]+=mx[x];
			++t;
		}
}
inline void dfs2(int x,int fa)
{
	int t=0;ans=max(ans,f[x][0]+g[x][0]);
	for(int i=la[x],v;i;i=edge[i].nx)
		if((v=edge[i].to)!=fa)
			g[v][0]=max(g[x][0]+dp[x][0][t],max(g[x][1]+dp[x][0][t],g[x][0]+dp[x][1][t])+edge[i].val),g[v][1]=g[x][0]+dp[x][0][t]+edge[i].val,dfs2(v,x),++t;
}
int main()
{
	g[1][0]=0,g[1][1]=-inf,scanf("%d",&n);
	for(int i=1,x,y,z;i<n;++i)scanf("%d%d%d",&x,&y,&z),add_edge(x,y,z);
	dfs(1,0),dfs1(1,0),dfs2(1,0),printf("%d",ans);
	return 0;
}