题解 CF1034B Little C Loves 3 II
题意
给定一个 \(n\times m\) 的棋盘,每次可以在上面放一对棋子 \((x,y)\),\((x',y')\),要求 \(|x-x'|+|y-y'|=3\),问最多可以放多少个棋子。
题解
本题中的「一对棋子」本质上只有如下两种摆放方式。
- \(||x-x'|-|y-y'||=3\)。

- \(||x-x'|-|y-y'||=1\)。
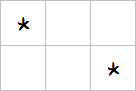
我们用这两种摆放方式可以凑出如下四种完整的棋盘。
- \(1\times6\)

- \(2\times4\)
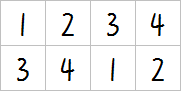
- \(2\times5\)
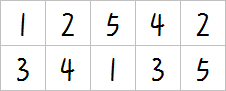
- \(3\times4\)
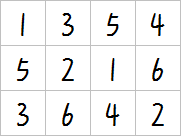
当 \(n\),\(m\) 足够小时,情况可能会有些特殊,我们先单独考虑这些情况。
情况 1 : \(n=1\) 或 \(m=1\)
不难发现只能使用第 \(1\) 种摆法。
每 \(6\) 个为一循环节,剩下 \(x\) 个格若多于 \(3\) 个又可以放 \(x-3\) 对。
所以答案为 \(\lfloor\dfrac{\max(n,m)}{6}\rfloor\times6+\max(0,\max(n,m)\mod6-3)\times2\)。
情况 2 : \(n=2\) 或 \(m=2\)
不妨设 \(n=2\)。
此时,若 \(m=4a+5b+6c\) 有自然数解,则 \(2\times m\) 的棋盘可以用 \(a\) 个 \(2\times4\) 的棋盘,\(b\) 个 \(2\times5\) 的棋盘和 \(2c\) 个 \(1\times6\) 的棋盘拼成,答案为 \(n\times m\)。
不难得出只有 \(m=2,3,7\) 时无解。
所以 \(n=m=2\) 时,答案为 \(0\);\(n=2,m=3\) 或 \(m=2,n=3\) 时,答案为 \(4\);\(n=2,m=7\) 或 \(m=2,n=7\) 时,答案为 \(12\);否则答案为 \(n\times m\)。
情况 3 : \(2|n,n\ge4,m\ge3\) 或 \(2|m,m\ge4,n\ge3\)
不妨 \(2|n\),\(n=2k\)。
若 \(m\ne3,7\),则可以由 \(k\) 个 \(2\times m\) 的棋盘拼成,答案为 \(n\times m\)。
若 \(m=7\),则可以用 \(k\) 个 \(2\times5\) 的棋盘和 \(1\) 个 \(2\times2k\) 的棋盘拼成,答案为 \(n\times m\)。
若 \(m=3,2|k\),设 \(k=2t\),则 \(n=4t\),可以用 \(t\) 个 \(3\times4\) 的棋盘拼成,答案为 \(n\times m\)。
若 \(m=3,2\nmid k\),设 \(k=2t+1\),则 \(n=4t+2\ge6\),可以用 \((t-1)\) 个 \(3\times4\) 的棋盘和 \(3\) 个 \(1\times6\) 的棋盘拼成,答案为 \(n\times m\)。
所以这类情况答案均为 \(n\times m\)。
情况 4 : \(2\nmid n,2\nmid m,n\ge3,m\ge3\)
不难发现答案一定不超过 \(n\times m-1\),且借助 \(1\times6\) 的棋盘可知一定情况下,\(n\times m\) 的棋盘与 \((n\mod6)\times(m\mod6)\) 的棋盘等价。
情况 4.1 : \(n\mod6=3\) 或 \(m\mod6=3\)
不妨设 \(n\mod6=3\),则这等价于 \(n=3,m\ge3\)。
对于任意大等于 \(3\) 的奇数 \(m\),我们总可以按如下方法递归地构造出如下图形。
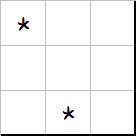
\(m=3\):
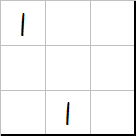
\(m=5\):
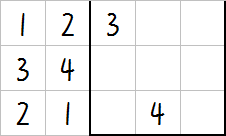
\(m=7\):
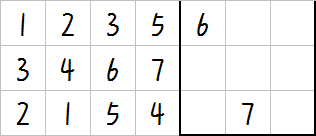
\(m=9\):
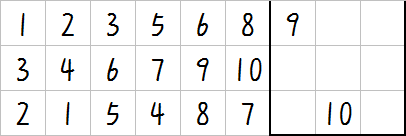
对于最后一个图形我们可以这样摆放棋子:
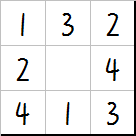
此时总共放了 \(n\times m-1\) 个棋子,达到最优状态,故答案为 \(n\times m-1\)。
情况 4.2 : \(n\mod6=5\) 或 \(m\mod6=5\)
不妨设 \(n\mod6=5\),则这等价于 \(n=5,m\ge3\)。
借助 \(2\times5\) 的棋盘可知,这等价于 \(1\times5\) 的棋盘。
而 \(1\times5\) 的棋盘上最多可摆放 \(4\) 个棋子,此时总共放了 \(n\times m-1\) 个棋子,达到最优状态,故答案为 \(n\times m-1\)。
情况 4.3 : \(n\mod6=1\) 且 \(m\mod6=1\)
这等价于 \(n=m=1\),此时总共放了 \(n\times m-1\) 个棋子,达到最优状态,故答案为 \(n\times m-1\)。
Code
#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL n,m,ans;
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0' || ch>'9')f|=(ch=='-'),ch=getchar();
while(ch>='0' && ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
x=f? -x:x;return ;
}
inline LL max(LL a,LL b)
{
return a>b? a:b;
}
int main()
{
read(n),read(m);
if(n==1 || m==1)return 0&printf("%lld",(max(n,m)/6)*6+max(0,(max(n,m)%6)-3)*2);
if(n==2 && m==2)return 0&printf("0");
if((!(n&1) && m>=3) || (!(m&1) && n>=3))return 0&printf("%lld",((n*m)/2-((n==2 && m==3) || (m==2 && n==3) || (n==2 && m==7) || (m==2 && n==7)))*2);
if((n%6)==3 || (m%6)==3)return 0&printf("%lld",((n*m)/2)*2);
if((n%6)==5 || (m%6)==5)return 0&printf("%lld",((n*m)/2)*2);
return 0&printf("%lld",((n*m)/2)*2);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号