回溯算法——n皇后问题

n皇后问题

Question
根据国际象棋的规则，皇后可以攻击与其处于同一行、同一列或一条斜线上的棋子，给定n个皇后和一个n x n大小的棋盘，寻找使得所有皇后之间无法互相攻击的摆放方案。

如下图所示，当n=4时，共可找到两个解。从回溯算法的角度看，n x n大小的棋盘共有\(n^2\)个格子，给出了所有的选择choices。在逐个放置皇后的过程中，棋盘状态在不断变化，每个时刻的棋盘就是状态state。

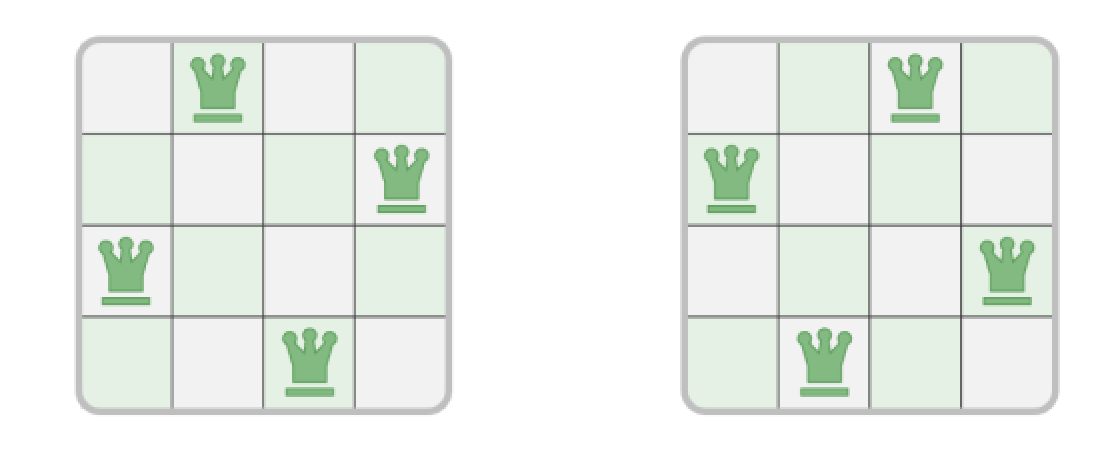
这里根据力扣51题描述，将字符.作为空棋盘格，字符Q作为皇后，如当n=4时，应当输出如下两个解

[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]

初次尝试，根据题目描述，通过一个二维n x n布尔数组valid控制每个棋盘格是否能够放入皇后，每次做出选择时，更新这个数组，根据放入的皇后的行列对对应对角线和列的valid置为false

通过变量idx控制递归中的行，每一次递归，对该行的每个可行的选择（根据valid）做选择

代码实现：

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<string> state;
        vector<vector<bool>> valid(n, vector<bool>(n, true));
        int idx = 0;
        backtrack(state, res, n, idx, valid);
        return res;
    }

    void backtrack(vector<string> &state, vector<vector<string>> &res, int n, int idx, vector<vector<bool>> valid){
        if(idx == n){
            res.emplace_back(state);
            return;
        }
        if(idx >= n) return;
        for(int i = 0; i < n; ++i){
            if(valid[idx][i]){
                auto new_valid = valid;
                makeChoice(idx, i, new_valid);
                state.emplace_back(createRow(i, n));
                backtrack(state, res, n, idx + 1, new_valid);
                state.pop_back();
            }
        }
    }

    void makeChoice(int i, int j, vector<vector<bool>> &valid){
        int n = valid.size();
        
        // 列
        for(int x = i + 1; x < n; ++x){
            valid[x][j] = false;
        }
        // 左下
        for(int x = i + 1, y = j - 1; x < n && y >= 0; ++x, --y){
            valid[x][y] = false;
        }
        // 右下
        for(int x = i + 1, y = j + 1; x < n && y < n; ++x, ++y){
            valid[x][y] = false;
        }
    }

    string createRow(int col, int n) {
        string row(n, '.');
        row[col] = 'Q';
        return row;
    }
};

优化

根据题目描述，皇后可以攻击同一行，同一列，同一斜线上的目标，即多个皇后不能存在同一行、同一列、同一对角线上。值得注意的是，对角线分为主对角线\和次对角线/两种

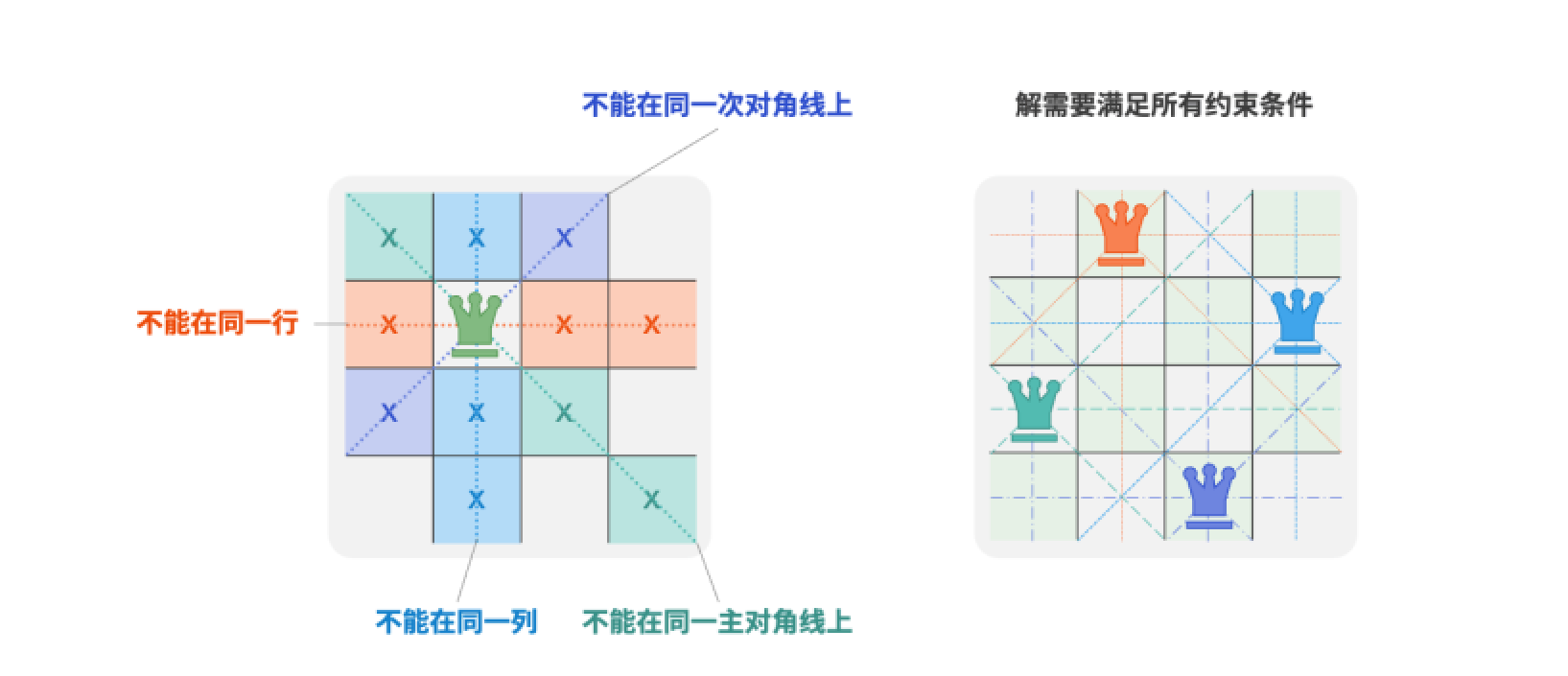
逐行放置策略

皇后的数量和棋盘行数都为n，因此我们容易得到一个推论：棋盘每行都允许且只允许放置一个皇后。

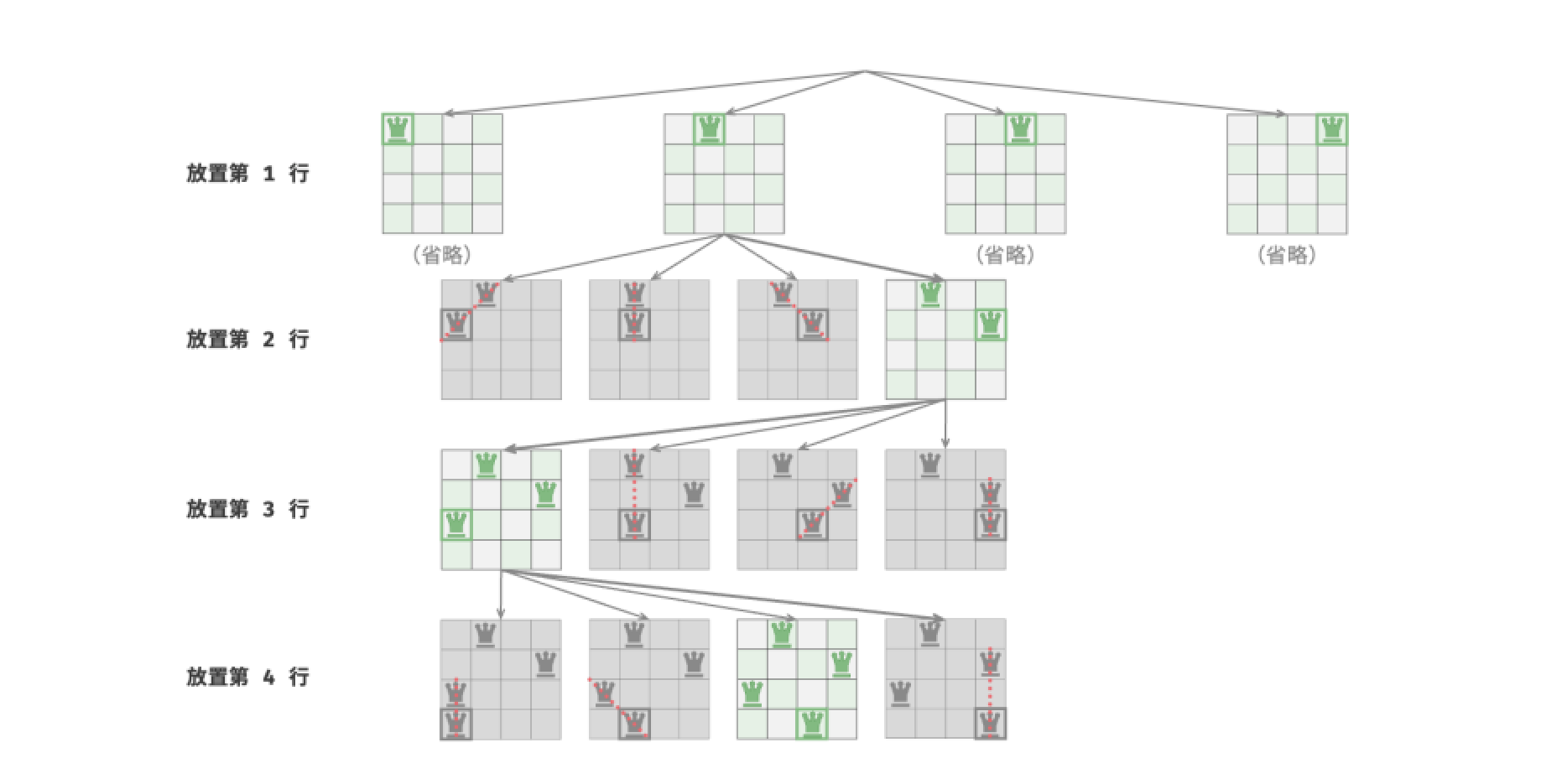
从本质上看，逐行放置策略起到了剪枝作用，它避免了同一行出现多个皇后的所有搜索分支

列与对角线剪枝

为满足列约束，我们可以利用一个长度为n的布尔型数组cols记录每一列是否有皇后。在每次决定放置前，我们通过cols将已有皇后的列进行剪枝，并在回溯中动态更新cols的状态

对于对角线，设棋盘中某个格子的行列索引为\((row,col)\)，选定矩阵中的某条主对角线，我们发现该对角线上所有格子的行索引减列索引都相等，即对角线上所有格子的\(row-col\)为恒定值

也就是说，如果两个格子满足\(row_1-col_1 = row_2-col_2\)，则它们一定处于同一条主对角线上。利用该规律，可以使用长度为\(2n-1\)的数组diags1来记录每条主对角线上是否有皇后

同理，次对角线上所有格子的\(row+col\)是恒定值。我们同样可以借助diags2来处理次对角线约束。

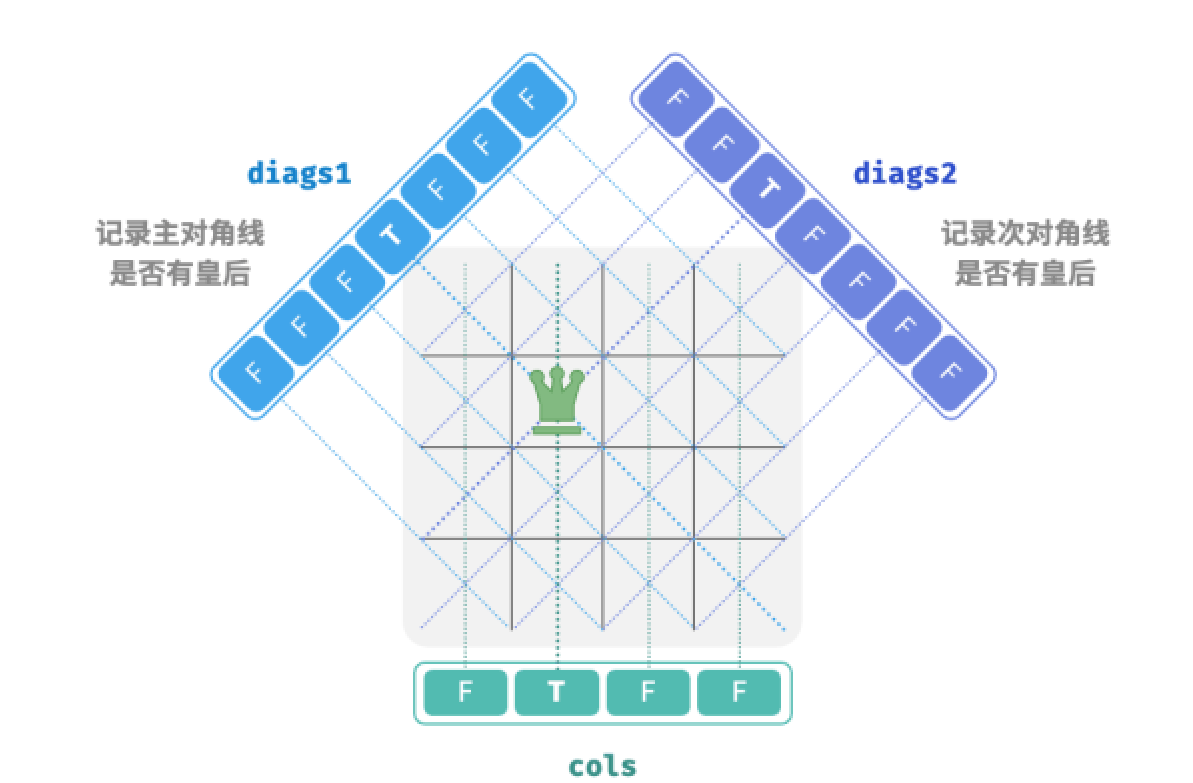
代码实现

注意，在\(n\)维方阵中，\(row-col\)的范围是\([-n+1,n-1]\), \(row+col\)的范围是\([0,2n-2]\)，主对角线和次对角线的数量都为\(2n-1\)

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<string> state(n, string(n, '.'));
        
        vector<bool> diags1(2 * n - 1, false); // 主对角线相减 值+(n-1) 保证索引在0 - 2n-1内
        vector<bool> diags2(2 * n - 1, false); // 次对角线相加
        vector<bool> cols(n, false); // 列
        int row = 0;
        backtrack(state, res, n, row, diags1, diags2, cols);
        return res;
    }
    /* 利用主对角线 row1 - col1 = row2 - col2 判断点在同一主对角线上 \ 对角线
        row1 + col1 = row2 + col2 判断点在同一次对角线上 / 对角线
    */
    void backtrack(vector<string> &state, vector<vector<string>> &res, int n, int row,
                vector<bool> &diags1, vector<bool> &diags2, vector<bool> &cols){
        if(row == n){
            res.emplace_back(state);
            return;
        }
        if(row >= n) return;

        for(int col = 0; col < n; ++col){
            // 该格的 主对角线 次对角线 列 都不存在皇后
            if(!diags1[row - col + n - 1] && !diags2[row + col] && !cols[col]){
                state[row][col] = 'Q';
                diags1[row - col + n - 1] = true;
                diags2[row + col] = true;
                cols[col] = true;
                backtrack(state, res, n, row + 1, diags1, diags2, cols);
                // 回溯
                state[row][col] = '.';
                diags1[row - col + n - 1] = false;
                diags2[row + col] = false;
                cols[col] = false;
            }
        }
    }
};

逐行放置\(n\)次，考虑列约束，则从第一行到最后一行分别有\(n、n-1、...、2、1\)个选择，使用\(O(n!)\)时间。当记录解时，需要复制矩阵state并添加进res，复制操作使用\(O(n^2)\)时间。因此，总体时间复杂度为\(O(n!·n^2)\)。实际上，根据对角线约束的剪枝也能够大幅度缩小搜索空间，因而搜索效率往往优于以上时间复杂度。

数组state使用\(O(n^2)\)空间，数组cols、diags1和diags2皆使用\(O(n)\)空间。最大递归深度为\(n\)，使用\(O(n)\)栈帧空间，因此空间复杂度为\(O(n^2)\)