回溯算法——子集和问题

子集和问题

无重复元素的情况

Question
给定一个正整数数组nums和一个目标正整数target，请找出所有可能的组合，使得组合中的元素和等于target。给定数组无重复元素，每个元素可以被选取多次。以列表形式返回这些组合，列表中不包含重复的组合

例如，输入集合{3,4,5}和目标整数9，解为{3,3,3},{4,5}，需要注意以下两点：

• 输入集合中的元素可以被无限次重复选取
• 子集不区分元素顺序，比如{4,5}和{5,4}是同一个子集

参考全排列解法

类似于全排列问题，我们可以把子集的生成过程想象成一系列选择的结果，并在选择过程中实时更新“元素和”，当元素和等于target时，就将子集记录到结果列表

与全排列问题不同的是，本题集合中的元素可以被无限次选取，因此无需借助selected布尔列表来记录元素是否已被选择，对全排列代码作小幅修改，可初步得到解题代码

/* 回溯算法：子集和 I */
void backtrack(vector<int>& state, int target, int total, vector<int>& choices, vector<vector<int>>& res) {
	// 子集和等于 target 时，记录解
	if (total == target) {
		res.push_back(state);
		return;
	}
	// 遍历所有选择
	for (size_t i = 0; i < choices.size(); i++) {
		// 剪枝：若子集和超过 target ，则跳过该选择
		if (total + choices[i] > target) {
			continue;
		}
		// 尝试：做出选择，更新元素和 total
		state.push_back(choices[i]);
		// 进行下一轮选择
		backtrack(state, target, total + choices[i], choices, res);
		// 回退：撤销选择，恢复到之前的状态
		state.pop_back();
	}
}
/* 求解子集和 I（包含重复子集） */
vector<vector<int>> subsetSumINaive(vector<int>& nums, int target) {
	vector<int> state; // 状态（子集）
	int total = 0; // 子集和
	vector<vector<int>> res; // 结果列表（子集列表）
	backtrack(state, target, total, nums, res);
	return res;
}

以上代码输入数组[3,4,5]和目标元素9，输出结果为[3,3,3],[4,5],[5,4]。虽然成功找出了所有和为9的子集，但其中存在重复的子集[4,5]和[5,4]

这是因为搜索的过程时区分选择顺序的，然而自己不区分选择顺序，先选4后选5与先选5后选4是不同的分支，但对应同一个子集

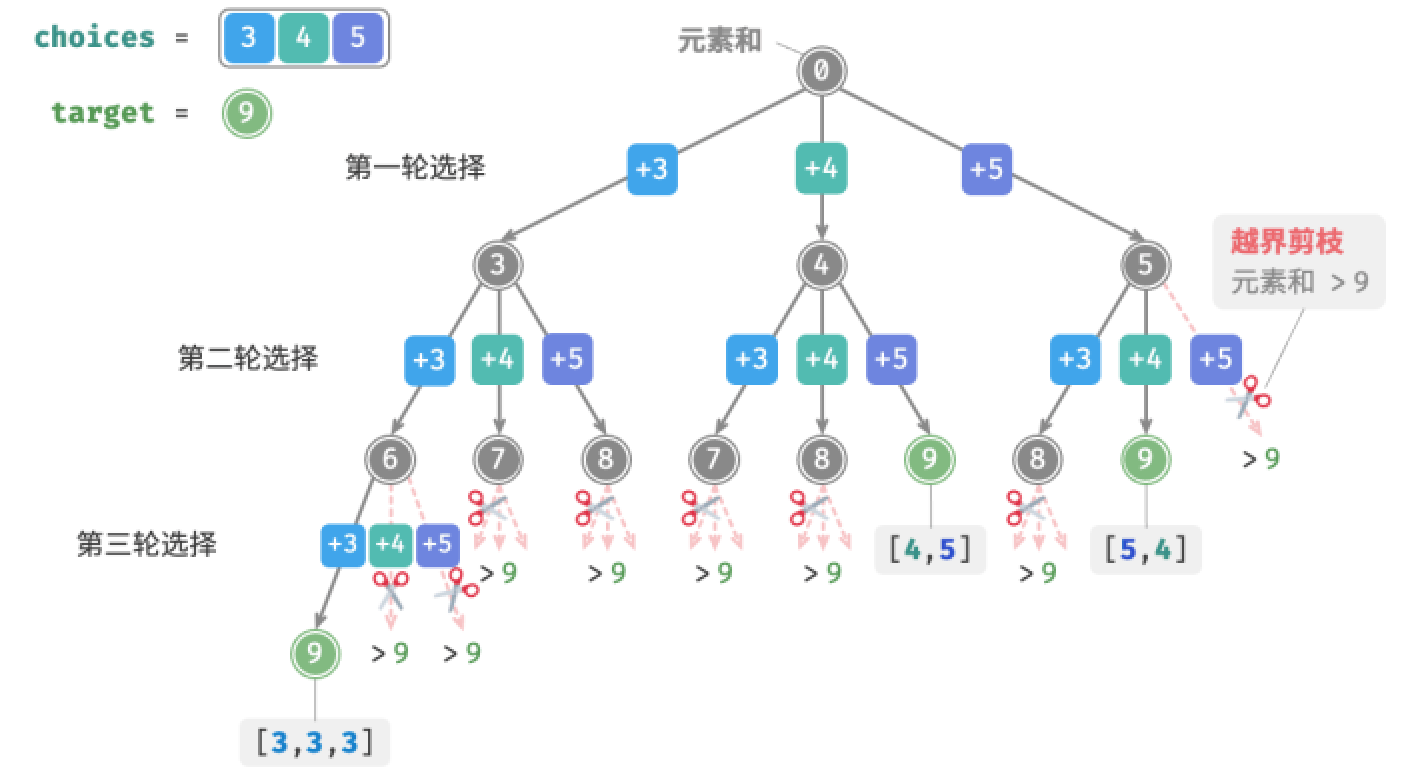
为去除重复子集，一种直接的思路是对结果列表进行去重。但这种方法效率很低，当数组元素较多，尤其当target较大时，搜索过程会产生大量的重复子集，比较子集的异同非常耗时，需要先排序数组，再比较数组中每个元素的异同

重复子集剪枝

我们考虑在搜索过程中通过剪枝进行去重。重复子集是在以不同顺序选择数组元素时产生的，例如以下情况：

• 1.当第一轮和第二轮分别选择3和4时，会生成包含这两个元素的所有子集，记为[3,4,...]。
• 2.之后，当第一轮选择4时，第二轮应该跳过3，因为该选择产生的子集[4,3...]和第1.步中生成的子集完全重复

在搜索过程中每一层的选择都是从左到右逐个尝试的，因此越靠右的分支被减掉的越多

总结来看，给定输入数组\([x_1,x_2,...,x_n]\)，设所搜过程中的选择序列为\([x_{i1},x_{i2},...,x_{im}]\)，则该选择序列需要满足\(i_1\leq i_2\leq...\leq i_m\)，不满足该条件的选择序列都会造成重复，应当剪枝

代码实现

为实现该剪枝，我们初始化变量start，用于指示遍历起始点。当做出选择\(x_i\)后，设定下一轮从索引\(i\)开始遍历。这样做旧可以让选择的序列满足\(i_1\leq i_2\leq...\leq i_m\)，从而保证子集唯一

除此之外，我们还对代码进行了以下两项优化：

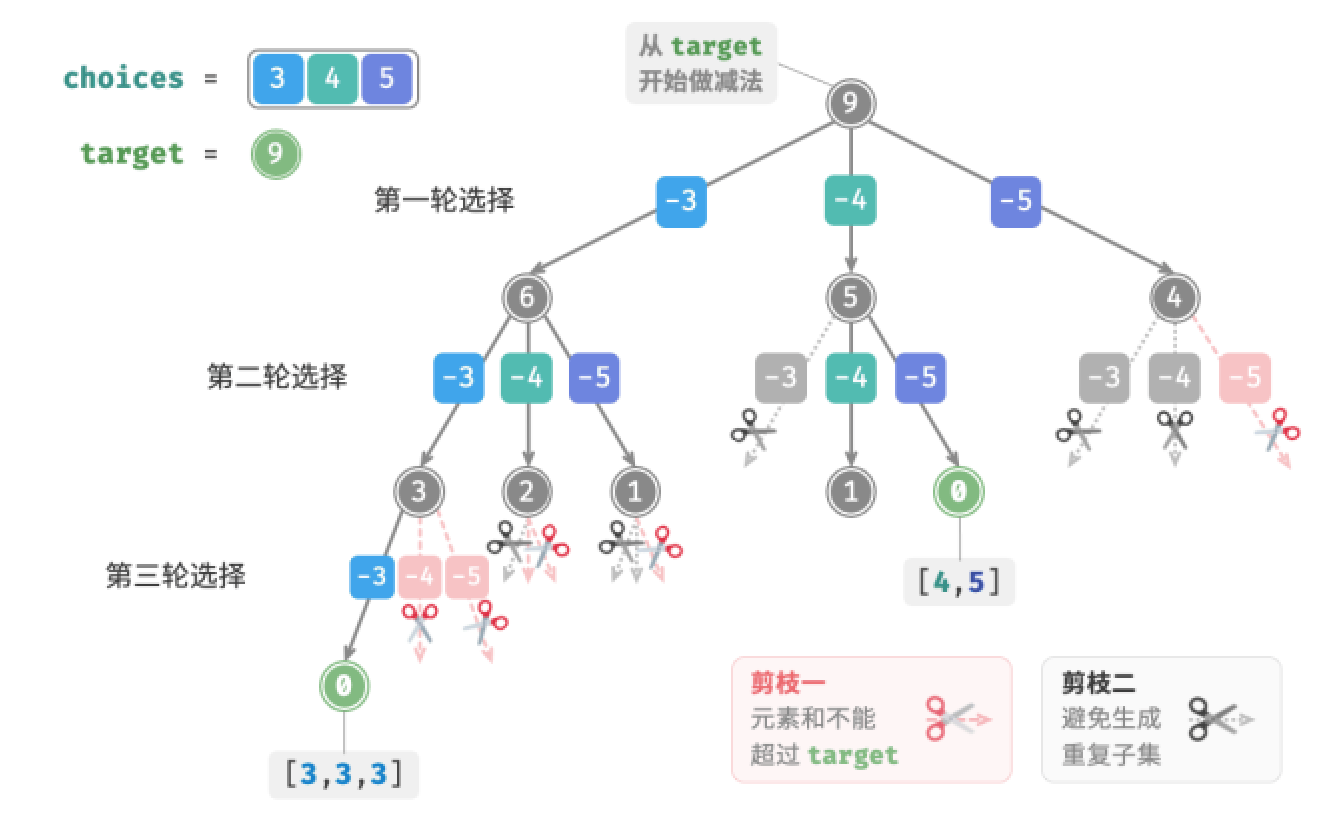
• 在开启搜索前，先将数组nums排序。在遍历所有选择时，当子集和超过target时直接结束循环，因为后边元素更大，其子集和一定超过target。
• 省去元素和这个变量total，通过在target上执行减法来统计元素和，当target等于0时，记录解。

/* 回溯算法：子集和 I */
void backtrack(vector<int>& state, int target, vector<int>& choices, int start, vector<vector<int>>& res) {
	// 子集和等于 target 时，记录解
	if (target == 0) {
		res.push_back(state);
		return;
	}
	// 遍历所有选择
	// 剪枝二：从 start 开始遍历，避免生成重复子集
	for (int i = start; i < choices.size(); i++) {
		// 剪枝一：若子集和超过 target ，则直接结束循环
		// 这是因为数组已排序，后边元素更大，子集和一定超过 target
		if (target - choices[i] < 0) {
				break;
		}
		// 尝试：做出选择，更新 target, start
		state.push_back(choices[i]);
		// 进行下一轮选择
		backtrack(state, target - choices[i], choices, i, res);
		// 回退：撤销选择，恢复到之前的状态
		state.pop_back();
	}
}
/* 求解子集和 I */
vector<vector<int>> subsetSumI(vector<int>& nums, int target) {
	vector<int> state; // 状态（子集）
	sort(nums.begin(), nums.end()); // 对 nums 进行排序
	int start = 0; // 遍历起始点
	vector<vector<int>> res; // 结果列表（子集列表）
	backtrack(state, target, nums, start, res);
	return res;
}

考虑重复元素的情况

Question
给定一个正整数数组nums和一个目标整数target，找出所有可能的组合，使得组合中的元素和等于target。给定的数组可能包含重复元素，每个元素只能使用一次。返回所有不重复的组合

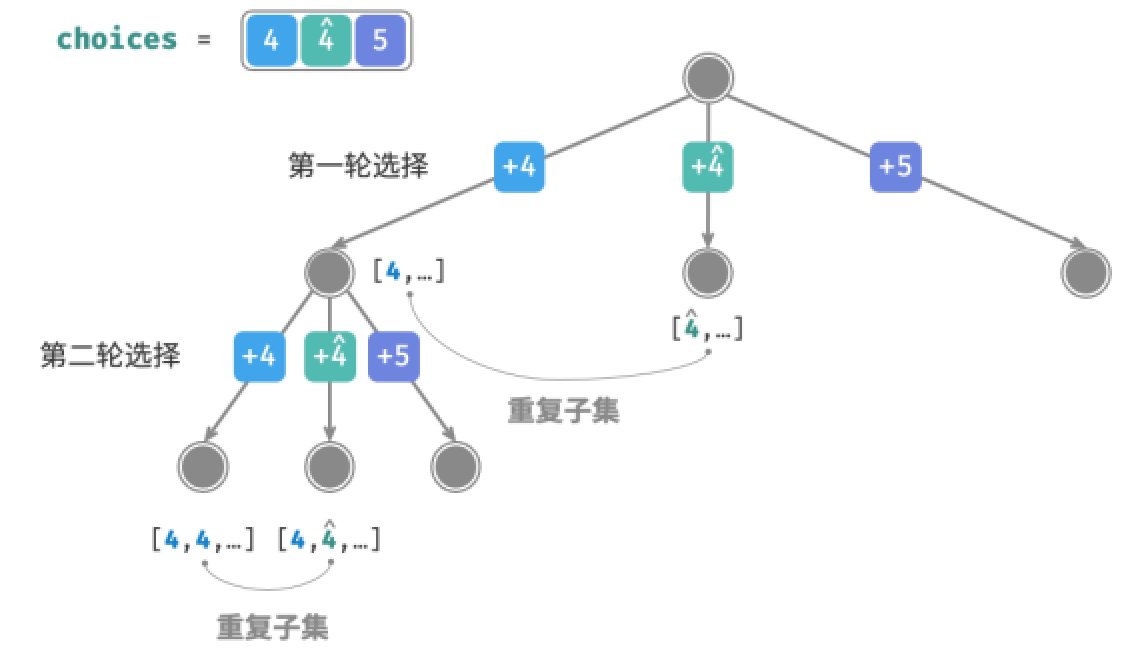
相比于上题，本题的输入数组可能包含重复元素，这引入了新的问题，如给定数组[4,4,5]和目标target9，则现有代码的输出结果为[4,5],[4,5]，出现了重复子集

造成这种重复的原因是相等元素在某轮中被多次选择，下图中，第一轮共有3个选择，其中两个都为4，会产生两个重复的搜索分支，从而输出重复子集；同理，第二轮的两个4也会产生重复子集。

相等元素剪枝

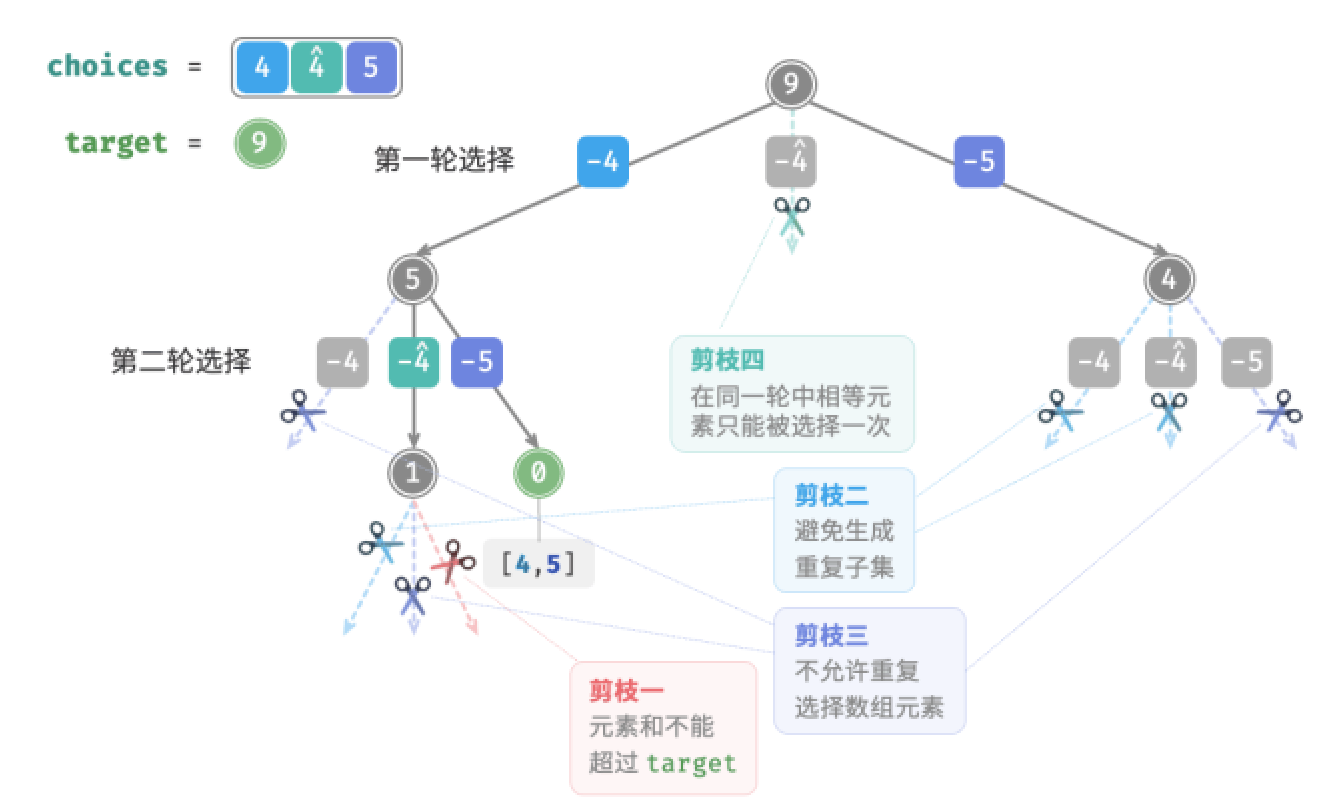
为解决此问题，我们需要限制相等元素在每一轮中只能被选择一次。实现方式比较巧妙：由于数组是已经排序的，因此相等元素都是相邻的。这意味着在某轮次选择中，若当前元素与其左边元素相等，则说明它已经被选择过，因此直接跳过当前元素

与此同时，此题规定每个数组元素只能被选择一次，我们也可以利用变量start来满足该约束：当做出选择\(x_i\)后，设定下一轮从索引\(i+1\)开始遍历，这样既能去除重复子集，也能避免重复选择元素

代码实现：

void backtrack(vector<int>& state, int target, vector<int>& choices, int start, vector<vector<int>>& res) {
	// 子集和等于 target 时，记录解
	if (target == 0) {
		res.push_back(state);
		return;
	}
	// 遍历所有选择
	// 剪枝二：从 start 开始遍历，避免生成重复子集
	// 剪枝三：从 start 开始遍历，避免重复选择同一元素
	for (int i = start; i < choices.size(); i++) {
		// 剪枝一：若子集和超过 target ，则直接结束循环
		// 这是因为数组已排序，后边元素更大，子集和一定超过 target
		if (target - choices[i] < 0) {
			break;
		}
		// 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
		if (i > start && choices[i] == choices[i - 1]) {
			continue;
		}
		// 尝试：做出选择，更新 target, start
		state.push_back(choices[i]);
		// 进行下一轮选择
		backtrack(state, target - choices[i], choices, i + 1, res);
		// 回退：撤销选择，恢复到之前的状态
		state.pop_back();
	}
}
/* 求解子集和 II */
vector<vector<int>> subsetSumII(vector<int>& nums, int target) {
	vector<int> state; // 状态（子集）
	sort(nums.begin(), nums.end()); // 对 nums 进行排序
	int start = 0; // 遍历起始点
	vector<vector<int>> res; // 结果列表（子集列表）
	backtrack(state, target, nums, start, res);
	return res;
}