回溯算法——全排列问题

全排列问题

全排列是回溯算法的一个典型应用，它的定义时在给定一个集合（如数组或字符串）的情况下，找出其中元素的所有可能的排列

示例：

输入数组	所有排列
[1]	[1]
[1,2]	[1,2], [2,1]
1,2,3]	[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]

无相等元素的情况

Question
输入一个整数数组，其中不包含重复元素，返回所有可能的排列。

从回溯算法的角度看，我们可以把生成排列的过程想象成一系列选择的结果。假设输入数组为[1,2,3]，如果我们先选择1，再选择3，最后选择2，则获得排列[1,3,2]。回退表示撤销一个选择，之后继续尝试其他选择。

从回溯代码的角度看，候选集合choices是输入数组中的所有元素，状态state是直至目前已被选择的元素。请注意，每个元素只允许被选择一次，因此state中的所有元素都应该是唯一的

如下图，我们可以将搜索过程展开成一颗递归树，树中的每个节点代表当前状态state。从根节点开始，经过三轮选择后到达叶子节点，每个叶子节点都对应一个排列

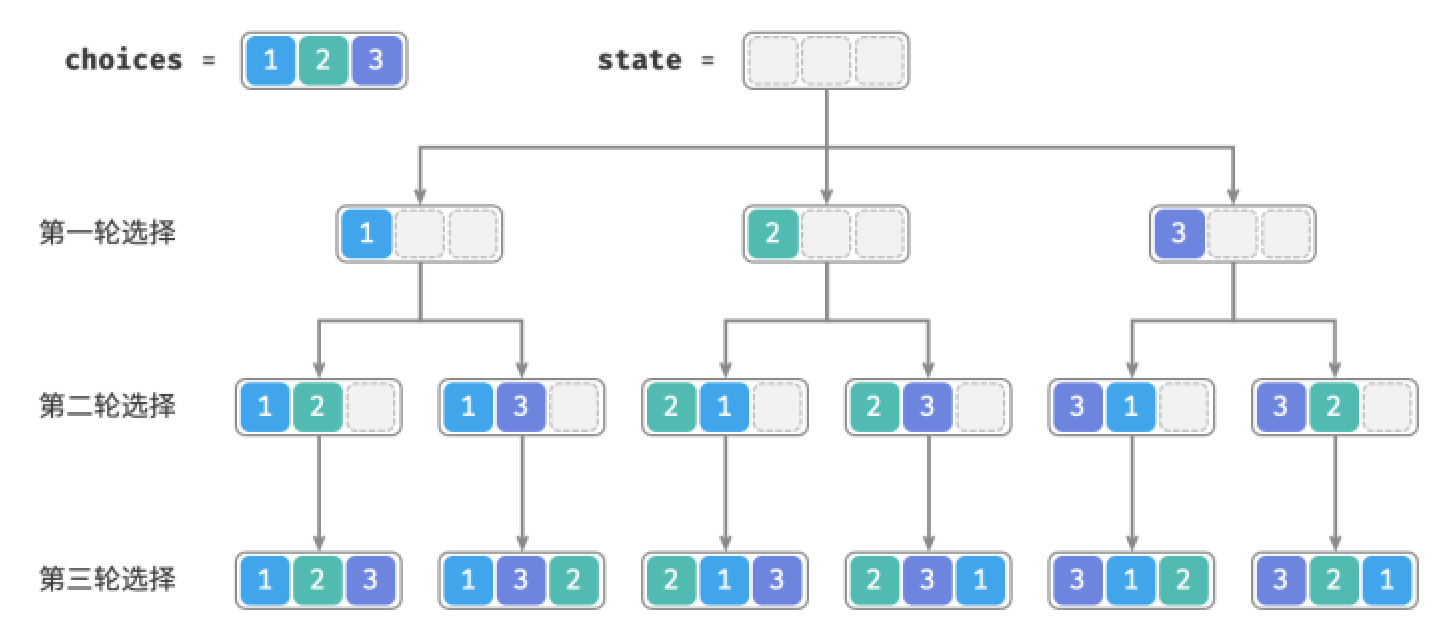
重复选择剪枝

为了实现诶个元素只被选择一次，我们考虑引入一个布尔型数组selected，其中selected[i]表示choices[i]是否已被选择，并基于它实现以下剪枝操作：

• 在做出选择choices[i]后，我们就将selected[i]赋值为True，代表它已被选择。
• 遍历选择列表choices时，跳过所有已被选择的节点，即完成剪枝

如下图，假设我们第一轮选择1，第二轮选择3，第三轮选择2，则需要在第二轮剪掉元素1的分支，第三轮剪掉元素1和元素3的分支。

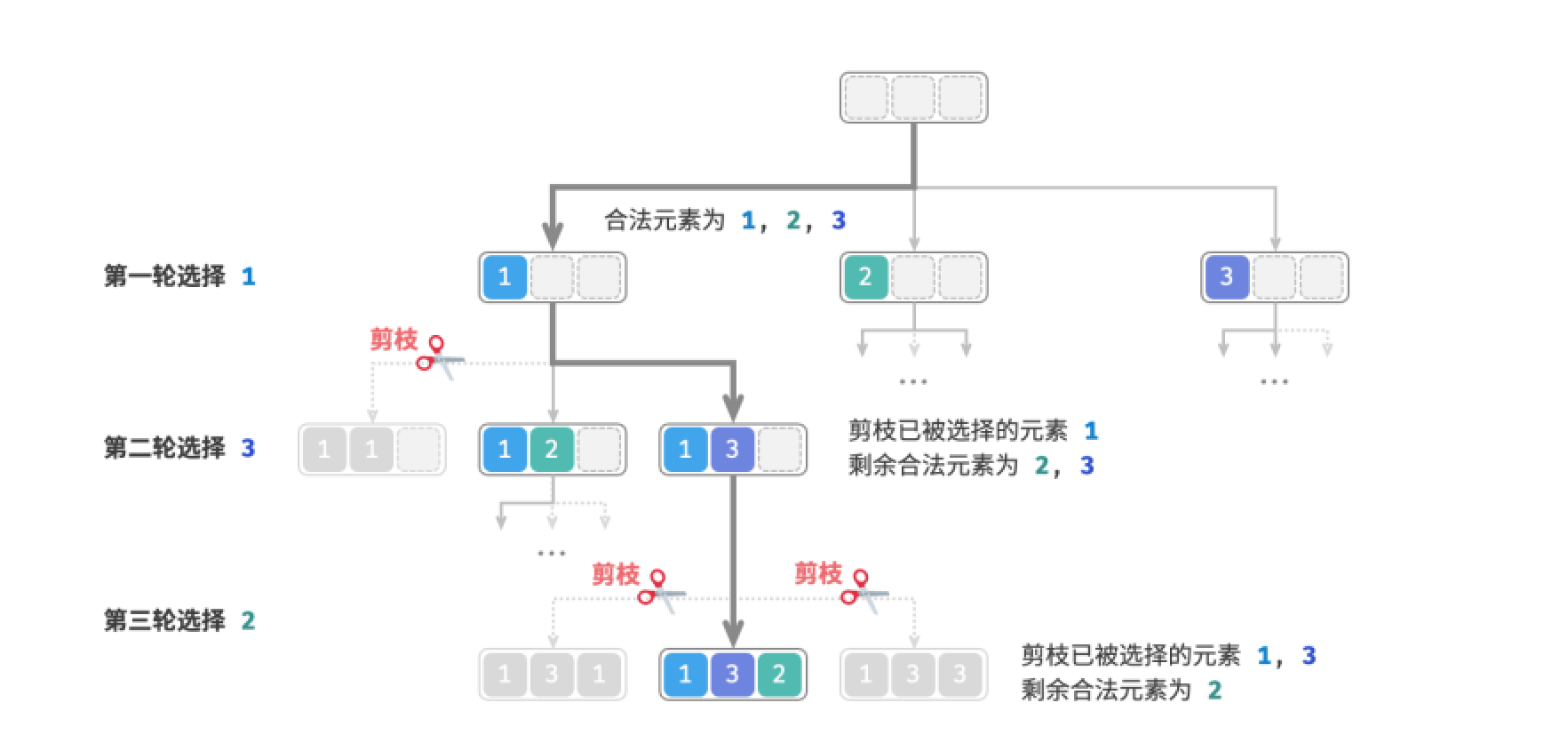
观察发现，该剪枝操作将搜索空间大小从\(O(n^n)\)减小至\(O(n!)\)

清楚以上信息后，我们就可以在框架代码中填写对应部分：

#include <string>
#include <iostream>
#include <vector>

using namespace std;

/* 全排列 I  回溯算法*/
void backtrackI(vector<int>& state, vector<int>& choices, vector<vector<int>>& res, vector<bool> &selected) {
	// 判断是否为解
	if (state.size() == choices.size()) {
		// 记录解
		res.emplace_back(state);
		return;
	}

	for (int i = 0; i < choices.size(); ++i) {
		// 剪枝 当元素未选择才做选择
		if (!selected[i]) {
			// 做出选择
			state.emplace_back(choices[i]);
			selected[i] = true;
			// 进行下一轮选择
			backtrackI(state, choices, res, selected);
			// 回退
			state.pop_back();
			selected[i] = false;
		}

	}
}
 
/* 全排列 I */
vector<vector<int>> permutationsI(vector<int> nums) {
	vector<int> state;
	vector<bool> selected(nums.size(), false);
	vector<vector<int>> res;
	backtrackI(state, nums, res, selected);
	return res;
}

void printVec(const vector<vector<int>>& vec) {
	for (vector<int> nums : vec) {
		for (int n : nums) {
			cout << n << " ";
		}
		cout << endl;
	}
}
int main() {
	vector<int> nums = { 1,2,3 };
	printVec(permutationsI(nums));
	return 0;
}

得到结果：

考虑相等元素的情况

Qusstion
输入一个整数数组，数组中可能包含重复元素，返回所有不重复的排列。

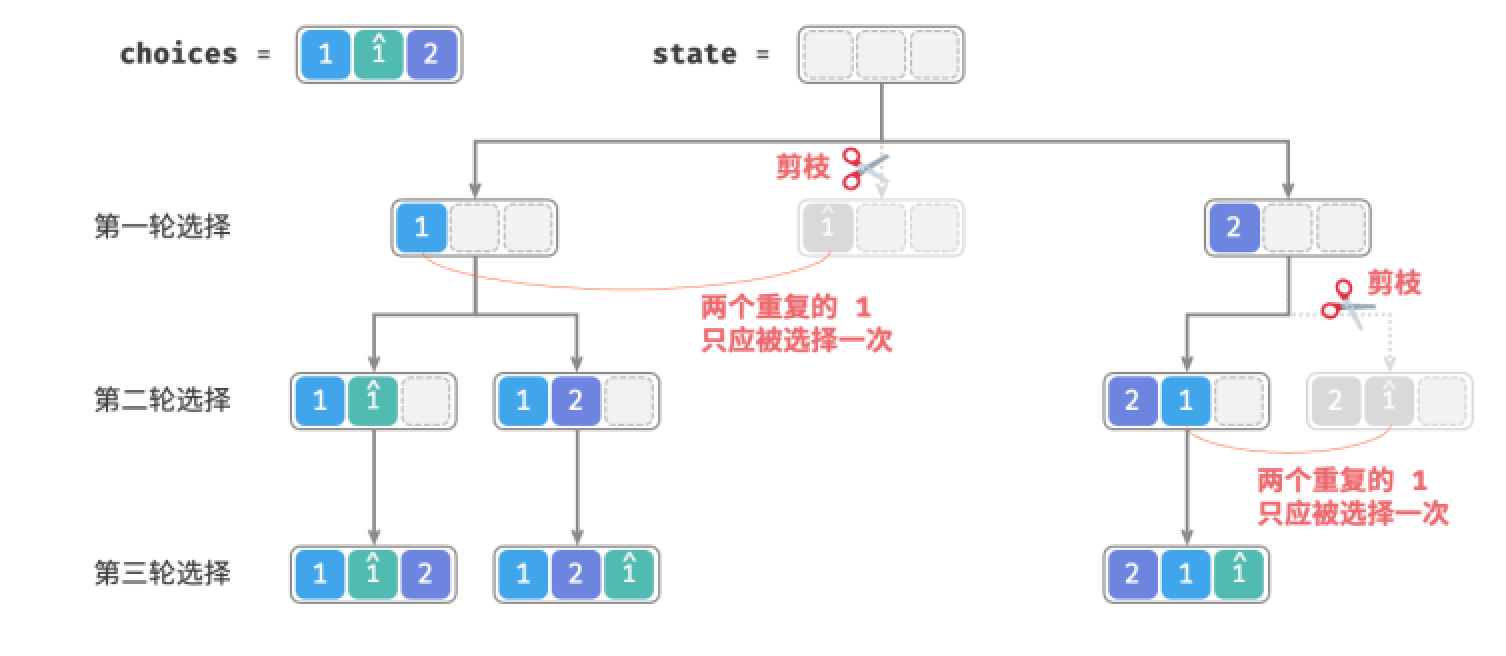
假设输入数组为[1,2,2]。为了方便区分两个重复的1，我们将第二个1记为\(1^{\hat{}}\)。

如下所示，前面的方法生成的排列有一半是重复的。

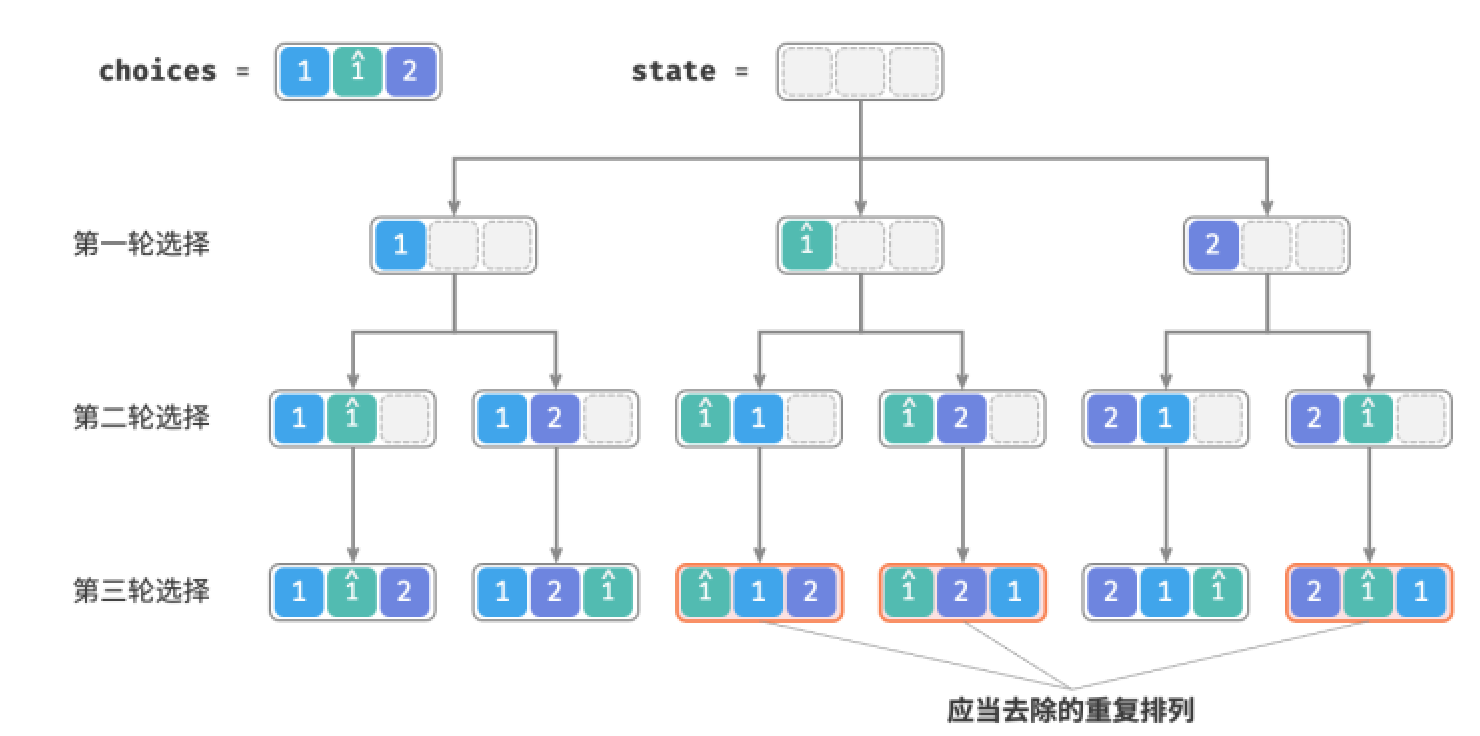
如何去除重复的排列呢，最直接地，考虑借助一个哈希表，直接对排列结果进行去重。然而这样做不够优雅，因为生成重复排列的搜索分支没有必要，应当提前识别并剪枝，这样可以进一步提升算法效率

相等元素剪枝

观察上图，在第一轮中，选择1或者选择1^{是等价的，在这两个选择下生成的所有排列都是重复的。因此应该把1}剪枝

同理在第一轮选择2之后，第二轮中的1和1^{也会产生重复分支，因此应将第二轮的1}剪枝

从本质上看，我们的目标是在某一轮选择中，保证多个相等的元素仅被选择一次。

代码实现

在上一题的基础上，我们考虑在每一轮选择中开启一个哈希表duplicated，用于记录该轮中已经尝试过的元素，并将重复元素剪枝

#include <string>
#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;

/* 全排列 II  回溯算法*/
void backtrack(vector<int>& state, vector<int>& choices, vector<vector<int>>& res, vector<bool>& selected) {
	if (state.size() == choices.size()) {
		// 记录解
		res.emplace_back(state);
		return;
	}
	unordered_set<int> duplicated;
	for (int i = 0; i < choices.size(); ++i) {
		// 剪枝  不允许重复元素 且 不允许重复选择相等元素
		if (!selected[i] && duplicated.find(choices[i]) == duplicated.end()) {
			state.emplace_back(choices[i]);
			selected[i] = true;
			duplicated.emplace(choices[i]);
			// 进入下一轮
			backtrack(state, choices, res, selected);
			// 回退
			state.pop_back();
			selected[i] = false;
		}
	}

}
/* 全排列 II */
vector<vector<int>> permutationsII(vector<int> nums) {
	vector<int> state;
	vector<bool> selected(nums.size(), false);
	vector<vector<int>> res;
	backtrack(state, nums, res, selected);
	return res;
}
void printVec(const vector<vector<int>>& vec) {
	for (vector<int> nums : vec) {
		for (int n : nums) {
			cout << n << " ";
		}
		cout << endl;
	}
}
int main() {
	vector<int> nums = { 1,2,3,3 };
	printVec(permutationsII(nums));
	return 0;
}

结果：

假设元素两两之间互不相同，则n个元素共有\(n!\)种排列，在记录结果时需要复制长度为n的列表，使用\(O(n)\)时间，因此时间复杂度为\(O(n!n)\)

最大递归深度为n，使用\(O(n)\)栈帧空间。selected使用\(O(n)\)空间。同一时刻最多共有n个duplicated，使用\(O(n^2)\)空间，因此空间复杂度为\(O(n^2)\)

对于该题，还有一种更优秀的解法，不借助哈希表，需要要求序列是有序的，所以需要提前排序

在有序的前提下，相同的元素被组合到了一块，对于数组[1,2,2,3]，剪枝中增加与前一项的相等判断，如果与前一项相等，且前一项的selected状态为fasle未使用，说明这个相同元素在之前的轮次中回退了，解已经记录，本轮次应该被剪枝

代码实现：

/* 全排列 II  回溯算法  不借助哈希表 但需要提前排序*/
void backtrack(vector<int>& state, vector<int>& choices, vector<vector<int>>& res, vector<bool>& selected) {
	if (state.size() == choices.size()) {
		// 记录解
		res.emplace_back(state);
		return;
	}
	for (int i = 0; i < choices.size(); ++i) {
		// 剪枝  不允许重复元素
		if (!selected[i]) {
			// 再次剪枝 当与前一项相同时，如果前一项未使用 说明这个相同元素已经被记录 回退了  需要剪枝
			if (i > 0 && choices[i] == choices[i - 1] && selected[i - 1] == false) continue;
			state.emplace_back(choices[i]);
			selected[i] = true;
			// 进入下一轮
			backtrack(state, choices, res, selected);
			// 回退
			state.pop_back();
			selected[i] = false;
		}
	}
}

这样优化后，空间复杂度仅需\(O(n)\)，对于时间复杂度，需要加上排序的时间复杂度\(O(nlog(n))\)，仍为原来的\(O(n!n)\)