算法与数据结构——栈

栈

栈（stack）是一种遵循先入后出逻辑的线性数据结构。

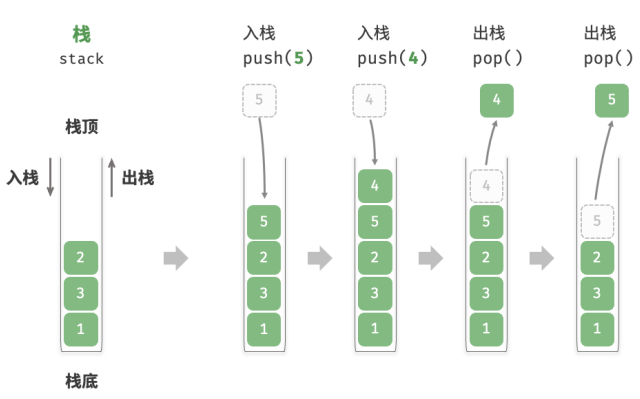
如图所示，我们将堆叠元素的顶部称为“栈顶”，底部称为“栈底”。将吧元素添加到栈顶的操作叫做“入栈”，删除栈顶的操作叫做“出栈”。

栈的常用操作

方法	描述	时间复杂度
push()	元素入栈（添加至栈顶）	O(1)
pop()	栈顶元素出栈	O(1)
peek()	访问栈顶元素	O(1)

通常情况下，我们可以直接使用编程语言内置的栈类，而一些语言没有专门提供栈类，我们可以将该语言的“数组”或“链表”当做栈来使用，并在程序逻辑上忽略与栈无关的操作。

	/*初始化栈*/
	stack<int> sta;

	/*元素入栈*/
	sta.push(1);
	sta.push(3);
	sta.push(2);
	sta.push(5);
	sta.push(4);

	/*访问栈顶元素*/
	int top = sta.top();
	cout << "栈顶元素：" << top << endl;

	/*元素出栈*/
	sta.pop();
	cout << "元素出栈" << endl;
	top = sta.top();
	cout << "栈顶元素：" << top << endl;

	/*获取栈的长度*/
	int sta_size = sta.size();
	cout << "栈长度：" << sta_size << endl;

	/*判断是否为空*/
	bool sta_empty = sta.empty();
	cout << "是否为空：" << sta_empty << endl;

栈的实现

为深入了解栈的运行机制，尝试自己实现一个栈类。

遵循先入后出的原则，因此我们只能在栈顶添加或删除元素。而数组和链表都可以在任意位置添加和删除元素，因此栈可以视为一种受限制的数组或链表。我们可以“屏蔽”数组或链表的部分无关操作，使其对外表现的逻辑符合栈的特性。

基于链表实现栈

使用链表实现栈时，我们可以将链表头节点视为栈顶，尾节点视为栈底。对于入栈操作，我们只需要将元素插入链表头部，这种节点插入方法称为“头插法”。而对于出栈操作只需要将头节点从链表中删除即可。

struct ListNode{
	int val;
	ListNode *next;
	ListNode(int x) :val(x), next(nullptr){}
	ListNode(int x,ListNode *next) :val(x), next(next){}
};

class LinkedListStack{
private:
	ListNode * stackTop; // 将头节点作为栈顶
	int stackSize;   // 栈长度
public:
	LinkedListStack(){
		stackTop = nullptr;
		stackSize = 0;
	}
	~LinkedListStack(){
		/*遍历链表每个节点 释放内存*/
		while (stackTop != nullptr){
			ListNode *tem = stackTop;
			stackTop = stackTop->next;
			delete tem;
		}
	}
	/*获取栈长度*/
	int size(){
		return stackSize;
	}

	/*判断栈是否为空*/
	bool isEmpty(){
		return (stackSize == 0);
	}

	/*入栈*/
	void push(int num){

		ListNode * node = new ListNode(num);
		node->next = stackTop;
		stackTop = node;
		stackSize++;
	}

	/*出栈*/
	int pop(){
		int num = top();
		ListNode * tem = stackTop;
		stackTop = stackTop->next;
		delete tem;
		stackSize--;
		return num;
	}

	/*访问栈顶元素*/
	int top(){
		if (isEmpty())
			throw out_of_range("栈为空");
		return stackTop->val;
	}
};

基于数组实现

使用数组实现栈时，我们可以将数组的尾部作为栈顶，入栈与出栈操作分别对应在数据尾部添加元素与删除元素，时间复杂度都为O(1)。

class ArrayStack{
private:
	vector<int> sta;
public:
	/*获取栈长度*/
	int size(){
		return sta.size();
	}
	/*判断栈是否为空*/
	bool isEmpty(){
		return (size() == 0);
	}
	/*入栈*/
	void push(int num){
		sta.push_back(num);
	}
	/*出栈*/
	int pop(){
		int num = top();
		sta.pop_back();
		return num;
	}
	/*访问栈顶元素*/
	int top(){
		if (isEmpty())
			throw out_of_range("栈为空");
		return sta[size()-1];
	}
};

两种实现对比

支持操作：

两种结果实现都支持栈定义中的各项操作。数组实现额外支持随机访问，但这已经超出了栈的定义范畴，因此一般不会用到。

时间效率：

在基于数组实现中，入栈和出栈操作都在预先分配好的连续内存中进行，具有很好的缓存本地性，因此效率较高。但如果入栈时超出数组容量，会触发扩容机制，导致该次入栈操作时间复杂度变为O(n)。

在基于链表实现中，链表的扩容十分灵活，不存在上述数组扩容时效率降低的问题。但是，入栈操作需要初始化节点对象并修改指针，因此效率相对较低。

空间效率

在初始化列表时，系统会为列表分配“初识容量”，该容量可能超出实际需求，并且扩容机制通常是按照特定的倍率（如2倍）进行扩容，扩容后的容量也可能超出实际需求。基于数组实现的栈可能造成一定的空间浪费。

基于链表实现的栈由于需要额外存储指针，因此链表节点占的空间相对较大。

栈的典型应用

• 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页，浏览器就会对上一个网页执行入栈，这样我们就可以通过后退操作回到上一个网页。后退操作实际上是在出栈，如果要同时支持后退和前进，那么需要两个栈来配合实现。
• 程序内存管理。每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会不断执行出栈操作。