采样之MCMC采样和M-H采样
在采样之马尔科夫链中我们讲到给定一个概率平稳分布π, 很难直接找到对应的马尔科夫链状态转移矩阵P。而只要解决这个问题，我们就可以找到一种通用的概率分布采样方法，进而用于蒙特卡罗模拟。本篇我们就讨论解决这个问题的办法：MCMC采样和它的易用版M-H采样
1.马尔科夫链的细致平稳条件
2. MCMC采样
假设我们已经有一个转移矩阵Q(对应元素为q(i,j)), 把以上的过程整理一下，我们就得到了如下的用于采样概率分布p(x)的算法。
3. M-H采样
4. M-H采样实例
为了更容易理解，这里给出一个M-H采样的实例。
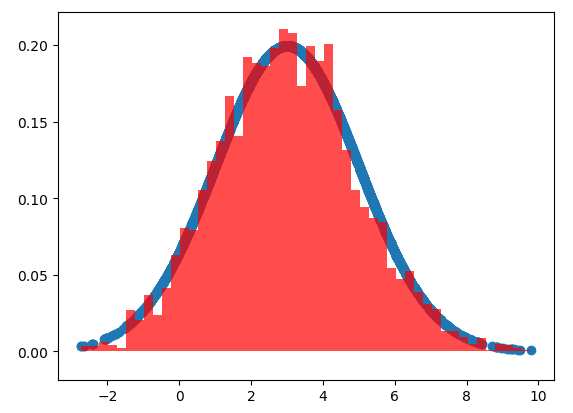
在例子里，我们的目标平稳分布是一个均值3，标准差2的正态分布，而选择的马尔可夫链状态转移矩阵Q(i,j)的条件转移概率是以i为均值,方差1的正态分布在位置j的值。这个例子仅仅用来让大家加深对M-H采样过程的理解。毕竟一个普通的一维正态分布用不着去用M-H采样来获得样本。
代码如下：
1 # coding: utf-8 2 import random 3 import math 4 from scipy.stats import norm 5 import matplotlib.pyplot as plt 6 7 # scipy.stats.norm.pdf(x, loc=0, scale=1) 8 # 输入x，返回概率密度函数;loc代表了均值,scale代表标准差 9 def norm_dist_prob(theta): 10 y = norm.pdf(theta, loc=3, scale=2) 11 return y 12 13 T = 5000 14 pi = [0 for i in range(T)] 15 sigma = 1 16 t = 0 17 while t < T-1: 18 t = t + 1 19 # rvs产生服从正太分布的一个样本，对随机变量进行随机取值 20 # rvs可以通过size参数指定输出的数组大小，即如果size=1 则产生一个样本值，如果size=2，则产生两个样本值。 21 pi_star = norm.rvs(loc=pi[t - 1], scale=sigma, size=1, random_state=None) 22 alpha = min(1, (norm_dist_prob(pi_star[0]) / norm_dist_prob(pi[t - 1]))) 23 24 u = random.uniform(0, 1) 25 if u < alpha: 26 pi[t] = pi_star[0] 27 else: 28 pi[t] = pi[t - 1] 29 30 # scatter是制作x与y的散点图 31 plt.scatter(pi, norm.pdf(pi, loc=3, scale=2)) 32 num_bins = 50 33 plt.hist(pi, num_bins, normed=1, facecolor='red', alpha=0.7) 34 plt.show()
输出的图中可以看到采样值的分布与真实的分布之间的关系如下:
参考：https://www.cnblogs.com/xbinworld/p/4266146.html
http://www.cnblogs.com/pinard/p/6638955.html
