二项分布和多项分布
首先二项分布和多项分布都是离散型分布
一 、二项式分布
（一）二项分布的基本概念
首先说一下伯努利试验，即n次独立重复试验，是在同样的条件下重复、相互独立进行的一种随机试验。
伯努利试验的特点是：
（1）每次试验中事件只有两种结果：事件发生或者不发生，如硬币正面或反面，患病或没患病；
（2）每次试验中事件发生的概率是相同的，注意不一定是0.5；
（3）n次试验的事件相互之间独立。
举个实例，最简单的抛硬币试验就是伯努利试验，在一次试验中硬币要么正面朝上，要么反面朝上，每次正面朝上的概率都一样p=0.5，且每次抛硬币的事件相互独立，即每次正面朝上的概率不受其他试验的影响。如果独立重复抛n=10次硬币，正面朝上的次数k可能为0,1,2,3,4,5,6,7,8,9,10中的任何一个，那么k显然是一个随机变量，这里就称随机变量k服从二项分布。
我们推导下随机变量X=k的分布律。显然0<=k<=n，n次抛硬币中获得k次正面，第1次正面在n次抛硬币中出现有n种方式，则第2次正面在n次抛硬币中出现有n-1种方式，以此类推，则出现的总可能方式是：n(n-1)...(n-k+1)种，如果我们并不考虑这k次正面出现的排列顺序，因此恰好出现k次的总可能性是n(n-1)...(n-k+1)/k！种，分子和分母同时乘以(n-k)！，则该式等于n！/(k！*(n-k)！)，也就是通常的组合公式C(n,k)=n！/(k！*(n-k)！)。
那么对于抛n次硬币，其中正面出现的次数是k，反面出现的次数必然为n-k次，不考虑顺序的情况下，则每一次恰好获得k次正面的概率是pk*(1-p)n-k，而n次试验中恰好出现k次正面的可能性是C(n,k)=n！/(k！*(n-k)！)种，因此，n次抛硬币中恰好出现k次的概率为：
P(X=k) = C(n,k) * pk*(1-p)n-k
这就是二项分布的分布律，即二项分布的的概率质量函数，记作X~B(n,p)，其中C(n,k)是组合数，在数学中也叫二项式系数，这就是二项分布名称的来历。
二项分布的均值：E(x)=np
二项分布的方差：Var(x)=np(1-p)
（二）二项分布的实现（python）
numpy给出的api是：
numpy.random.RandomState.binomial(n, p, size=None)
表示对一个二项分布进行采样（size表示采样的次数），参数中的n,p分别对应于公式中的n,p，函数的返回值表示n中成功（success）的次数（也即k）。我们以一个具体的实例进行阐释：
说野外正在进行9（n=9）口石油勘探井的发掘工作，每一口井能够开发出油的概率是0.1（p=0.1）。请问，最终所有的勘探井都勘探失败的概率？
我们手动用公式计算得：
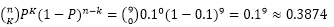
python实现如下：
import numpy as np
n, p = 9, .1
a=sum((np.random.binomial(n, p, size=30000)==0))/30000.
print a
运行结果为：0.387333333333
二、多项式分布
（一）基本概念
多项式分布是指单次试验中随机变量的取值不在是0-1，而是有多种离散值可能（1，2，3，4.....k）。比如投6个面的骰子试验，N次试验结果服从K=6的多项分布。其中：
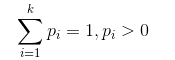
多项分布的概率密度函数为：
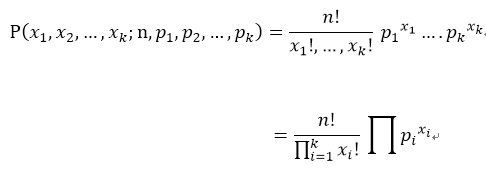
其中：
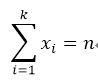
（二）例子
假设萤火虫对食物的喜欢程序，我们给三种选择：花粉，蚜虫，面团。假设20%的萤火虫喜欢花粉，35%的萤火虫喜欢蚜虫，45%的萤火虫喜欢面团。我们对30只萤火虫做实验，发现8只喜欢花粉，10只喜欢蚜虫，12只喜欢面团，这件事的概率为：
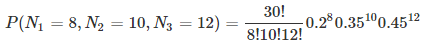
参考来源：
https://blog.csdn.net/qq280929090/article/details/53156655
https://blog.csdn.net/lanchunhui/article/details/50172659
