AtCoder Regular Contest 069 F-Flags

Flags

题意：N 个 flag，第 \(i\) 个在 \(x_i\) 或 \(y_i\) 坐标上，求一种方案，使得每个 flag 之间的最小距离最大。

\(2\le N \le 10^4, 1\le x_i, y_i \le 10^9\)

---

不妨设 \(a[i] = x_i, a[i+n] = y_i\) ，这样可以方便的取出同组元素。

排序后，为了定位到原位置，需要使用 pair 去存放每个坐标。

我们首先二分枚举距离 \(d\)，考虑排序后的数组 \(a\) , 对于 \(a[i]\)，它在原数组中的位置是 \(x\)，对应的另一个位置可用 y = x>=n?x-n:x+n 来计算。

如果最终 \(a[i]\) 位置被选择，那么范围 \([l,i-1], [i+1,r]\) 中的其他位置都不能够被选择（这个范围内的位置与 \(a[i]\) 距离都不超过 \(d\)）。这是一个 2-SAT 问题，该类问题可以转换为统一的形式：「若变量 \(A_i\) 赋值为 \(A_{i,p}\)，那么变量 \(A_j\) 必须赋值为 \(A_{j,q}\)」，其中 \(p,q\in {0, 1}\) 。

而上面的逻辑并不统一（形如：一个位置选择，若干个位置不选择），所以我们换种说法，如果 \(a[i]\) 的同组的另一个位置不被选择，那么 \([l, i-1], [i+1, r]\) 中的其他位置也不能选择。由此，我们可以从一个点向两段连续区间连边，然后跑 tarjan 判断 \(x\) 是否与 \(y\) 是否在同一个强连通分量中，进而判定是否合法。

但这样的复杂度很高 \((N^2 \log MAX)\)。

由于是一个点向两段区间中的每个点连边，那么不妨用线段树来将这两段大区间分解成若干端小区间，然后只需要与这些小区间在线段树中对应的节点连边即可。（其实就是线段树中的叶子节点，向若干个节点连边）。

而这一组连边，不会超过 \(\log N\)。

举个例子：

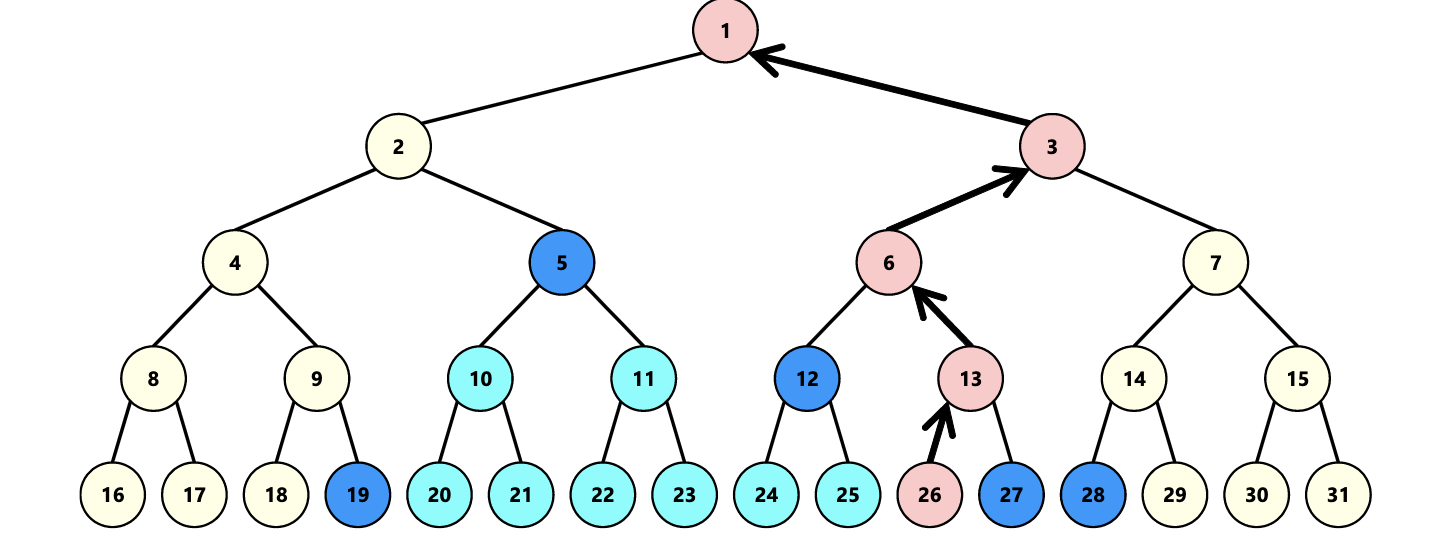
如上图所示，如果 26 被选择，然后 [19, 25], [27, 28] 这两个区间内的点不能够被选择，那么我们只需要找到与 26 同组的另外一个节点在线段树上的映射，然后与图中深蓝色的节点连边即可。

另外，在线段树上，父节点也需与两个子节点连边，因为这种「不选择性」是需要传递的。

所以，你需要构建线段树时，将父节点与子节点连边，另外你需要使得原数组中的位置映射到线段树的叶子节点编号，便于处理。总体复杂度 \(O(N\log N \log MAX)\)

typedef pair<int,int> pii;
typedef pair<long long, long long> pll;

constexpr int N = 80010, M = 2000010;
int n, pos[N], id[N];
vector<pii> a;
int tr[N], maxp;

// tarjan 板子
int head[N], ver[M], nxt[M], dfn[N], low[N];
int st[N], ins[N], c[N];
int tot, num, top, cnt;
void add(int x, int y){
    ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
}
void tarjan(int x){
    dfn[x] = low[x] = ++num;
    st[++top] = x, ins[x] = 1;
    for(int i=head[x]; i; i=nxt[i]){
        if(!dfn[ver[i]]){
            tarjan(ver[i]);
            low[x] = min(low[x], low[ver[i]]);
        }else if(ins[ver[i]]) 
            low[x] = min(low[x], dfn[ver[i]]);
    }
    if(dfn[x] == low[x]){
        cnt ++;int y;
        do{
            y = st[top--], ins[y] = 0;
            c[y] = cnt;
        }while(x != y);
    }
}

// 线段树构建
void build(int p, int l, int r) {
    maxp = max(p, maxp);
    if(l == r) {
        // 原数组位置映射到线段树的叶子结点上
        pos[a[l].second] = p;
        return;
    }
    int m = (l + r) / 2;
    build(p * 2, l, m);
    build(p * 2 + 1, m + 1, r);
    // 父指向子
    add(p, p * 2); add(p, p * 2 + 1);
}

// x 结点与 [L, R] 区间的线段树节点连边
void change(int p, int l, int r, int L, int R, int x) {
    if(L > R) return;
    if(l >= L && r <= R) {
        add(x, p);
        return;
    }
    int m = (l + r) / 2;
    if(L <= m) change(p * 2, l, m, L, R, x);
    if(R > m) change(p * 2 + 1, m + 1, r, L, R, x);
}

void init() {
    memset(head, 0, sizeof head);
    memset(low, 0, sizeof low);
    memset(dfn, 0, sizeof dfn);
    memset(c, 0, sizeof c);
    tot = num = top = cnt = 0;
}

bool check(int dis) {
    init();
    build(1, 0, 2 * n - 1);
    
    for(int i = 0; i < 2 * n; i++) {
        int l = a[i].first - dis + 1;
        int r = a[i].first + dis - 1;
        int L = lower_bound(a.begin(), a.end(), make_pair(l, 0)) - a.begin();
        int R = upper_bound(a.begin(), a.end(), make_pair(r, INT_MAX)) - a.begin() - 1;

        // a[i].second 为排序后第 i 个数对应的原位置，与它同组的另一个位置定义为 x：
        int x = a[i].second < n ? a[i].second + n : a[i].second - n;

        // 然后取其在线段树上的结点，所有的连边都是在线段树节点上进行的。
        x = pos[x];
        change(1, 0, 2 * n - 1, L, i - 1, x);
        change(1, 0, 2 * n - 1, i + 1, R, x);
    }
    for(int i = 1; i <= maxp; i ++) {
        if(!dfn[i]) tarjan(i);
    }

    // 2 - SAT 判定
    for(int i = 0; i < n; i++){
        if(c[pos[i]] == c[pos[i + n]]) return false;
    }
    return true;
}

void solve() {
    cin >> n;
    a.resize(2 * n);
    for(int i = 0; i < n; i++){
        cin >> a[i].first >> a[i + n].first;
        a[i].second = i; a[i + n].second = i + n;
    }
    sort(a.begin(), a.end());
    
    int l = 0, r = 1E9;
    while(l < r) {
        int m = (l + r + 1) / 2;
        if(check(m)) l = m;
        else r = m - 1;
    }
    cout << l << endl;
}