重温概率学（一）期望、均值、标准差、方差

概率

随机变量：实验的结果称为随机变量。
随机变量分为：

• 离散随机变量：如骰子。
• 连续随机变量：如时间范围。实数范围（包含有理数和无理数）

因为随机变量可以取不同的值，所以产出了概率分布的概念，统计学家用概率分布描述不同随机变量发生的概率。因此有：

• 离散型概率分布
• 连续型概率分布

期望和均值

如果我们掷了无数次的骰子，然后将其中的点数进行相加，然后除以他们掷骰子的次数得到均值，这个有无数次样本得出的均值就趋向于期望。

均值是针对样本发生的频率而言的，期望是针对样本发生的概率分布而言的，所以总结后便是：
概率是频率随样本趋于无穷的极限。
期望是均值随样本趋于无穷的极限。
上述表达的意思其实也就是弱大数定理

对于期望的理解：
理解1:
期望是反应样本平均值的指标，但是个体信息被压缩，所以看一个期望值的指标，需要采用“期望+数量”组合的方式去调研。

理解2:
平均数是根据实际结果统计得到的随机变量样本计算出来的算术平均值，和实验本身有关，而数学期望是完全由随机变量的概率分布所确定的，和实验本身无关。

实验的多少是可以改变平均数的，而在你的分布不变的情况下，期望是不变的。

期望（均值）、方差、标准差

 

 

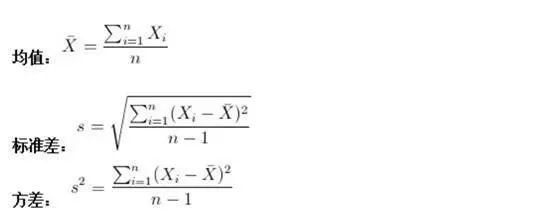
方差：在概率论和数理统计中,方差（英文Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度.方差越大，随机变量的结果越不稳定。常用来评估风险。
标准差：概念和方差一样，都是表示样本的离散程度。

标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差，代表一组数据里大部分的数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。（eg：两组数的集合 {1, 4, 9, 14} 和 {5, 6, 8, 9} 其平均值都是7，但第二个集合里的数字明显与7距离“更近”，通过公式算出第一个集合的标准差约为4.9，第二个约为1.5。）

为什么引入标准差？
因为在实践中，我们发现相当多的数据都呈现近似于“正态分布”。在正态分布图中，均值可以告诉我们中间的峰值是多少，而标准差则决定了宽度。

反过来正态分布也可以用来解释标准差：在一个标准正态分布中，数字出现的概率是固定的。

在方差和标准差之间如何选择？
方差只是计算标准差过程中产生的一个中间值，但是大多数情况下并不需要此中间值，而是采用了标准差，原因如下：
（1）表示离散程度的数字与样本数据点的数量级一致，更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例，其方差约为41，而标准差则为6.4；两者相比较，标准差更适合人理解。
（2）表示离散程度的数字单位与样本数据的单位一致，更方便做后续的分析运算。
（3）在样本数据大致符合正态分布的情况下，标准差具有方便估算的特性：66.7%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内，而99%的数据点将会落在平均值前后3个标准差的范围内。