第7讲、残差连接与层归一化：原理、结构与工程实践

深度神经网络的训练稳定性和表达能力是现代人工智能模型（尤其是 Transformer 架构）成功的关键。残差连接（Residual Connection）和层归一化（Layer Normalization）作为两项核心技术，极大地推动了深层网络的可训练性和泛化能力。本文系统梳理这两项技术的原理、结构、对比及其在 Transformer 等模型中的工程实践。

1. 残差连接（Residual Connection）

1.1 定义与数学表达

残差连接是一种跳跃连接（skip connection），其核心思想是让输入信号绕过一个或多个网络层，与输出直接相加：

1.2 作用与优势

缓解梯度消失/爆炸：为深层网络提供直接的梯度传递路径。
信息保留：允许网络在必要时直接保留输入信息，避免退化。
优化更容易：即使子层未学到有用变换，网络也能维持性能。

1.3 工程应用

残差连接最早由 ResNet（2015）提出，现已成为 Transformer、UNet 等主流深度模型的标准组件。

2. 层归一化（Layer Normalization）

2.1 定义与公式

层归一化对每个样本的所有特征维度进行标准化，公式如下：

2.2 作用与适用场景

提升训练稳定性：缓解梯度爆炸/消失，提升收敛速度
适合序列建模：对每个样本独立归一化，适用于 RNN、Transformer 等

2.3 与 BatchNorm 对比

特性	LayerNorm	BatchNorm
归一化维度	每个样本的所有特征维度	每个特征维度的所有样本
是否受 batch size 影响	否	是
适用场景	RNN、Transformer	CNN、MLP

3. Transformer 中的归一化与残差结构

Transformer 子层的标准结构如下：

3.1 结构对比与演化

模式	归一化位置	优势与劣势
Pre-Norm	子层前	梯度路径清晰，训练更稳定，适合深层网络
Post-Norm	残差加法后	原始 Transformer 采用，深层时易梯度消失

现代主流 Transformer（如 GPT-2/3/4、BERT 优化版、T5）普遍采用 Pre-Norm 结构，显著提升了深层模型的可训练性和收敛速度。

3.2 结构图示

Post-Norm:
    x
     \
      +-------+     
      | Add   |       
      +-------+
          |
   +-------------+
   | LayerNorm   |
   +-------------+
          |
       Output

Pre-Norm:
    x ------------------+
                        |
   +-------------+      |
   | LayerNorm   |      |
   +-------------+      |
          |             |
     +--------+         |
     | Sublayer|        |
     +--------+         |
          |             |
         Add <----------+
          |
       Output

你的请求是“再帮我添加一下，这2个技术在架构里的位置”。
下面是建议插入到第3节（Transformer中的归一化与残差结构）后的内容，你可以直接复制粘贴到合适位置：

3.3 典型架构中的位置说明

在 Transformer 及类似深度学习架构中，残差连接和层归一化的典型位置如下：

残差连接：用于每个子层（如自注意力层、前馈网络层）输入与输出之间，直接将输入与子层输出相加，形成跳跃路径。
层归一化：通常与残差连接配合，放置在子层前（Pre-Norm）或残差加法后（Post-Norm），对每个子层的输入或输出进行归一化处理。

以 Transformer 编码器子层为例，结构如下：

# 以 Pre-Norm 为例
Input
  │
LayerNorm
  │
Sublayer (Self-Attention or FFN)
  │
Add (Residual Connection)
  │
Output

在解码器中，残差连接和层归一化同样应用于自注意力、交互注意力和前馈网络等子层。

这种设计保证了深层网络的信息流动和训练稳定性，是现代深度学习模型不可或缺的结构组件。

3.4 简单代码实现案例

🔵 3.4.1. Post-Norm 实现（原始 Transformer 结构）

class PostNormBlock(nn.Module):
    def __init__(self, dim):
        super(PostNormBlock, self).__init__()
        self.linear = nn.Linear(dim, dim)
        self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        out = self.linear(x)
        out = x + out               # 残差连接
        out = self.norm(out)        # 后归一化
        return out

🟢 3.4.2. Pre-Norm 实现（现代优化结构）

class PreNormBlock(nn.Module):
    def __init__(self, dim):
        super(PreNormBlock, self).__init__()
        self.linear = nn.Linear(dim, dim)
        self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        out = self.norm(x)          # 先归一化
        out = self.linear(out)
        out = x + out               # 残差连接
        return out

4. 工程实践与可视化对比

以下代码演示了 Pre-Norm 与 Post-Norm 的结构差异及其对向量的影响，可用于直观理解两种归一化方式在残差结构中的作用。

import streamlit as st
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# Pre-Norm Block
class PreNormBlock(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.linear = nn.Linear(dim, dim)
        self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        x_norm = self.norm(x)
        sublayer_out = self.linear(x_norm)
        residual = x + sublayer_out
        return x_norm, sublayer_out, residual

# Post-Norm Block
class PostNormBlock(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.linear = nn.Linear(dim, dim)
        self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        sublayer_out = self.linear(x)
        residual = x + sublayer_out
        out = self.norm(residual)
        return sublayer_out, residual, out

# Streamlit 可视化界面
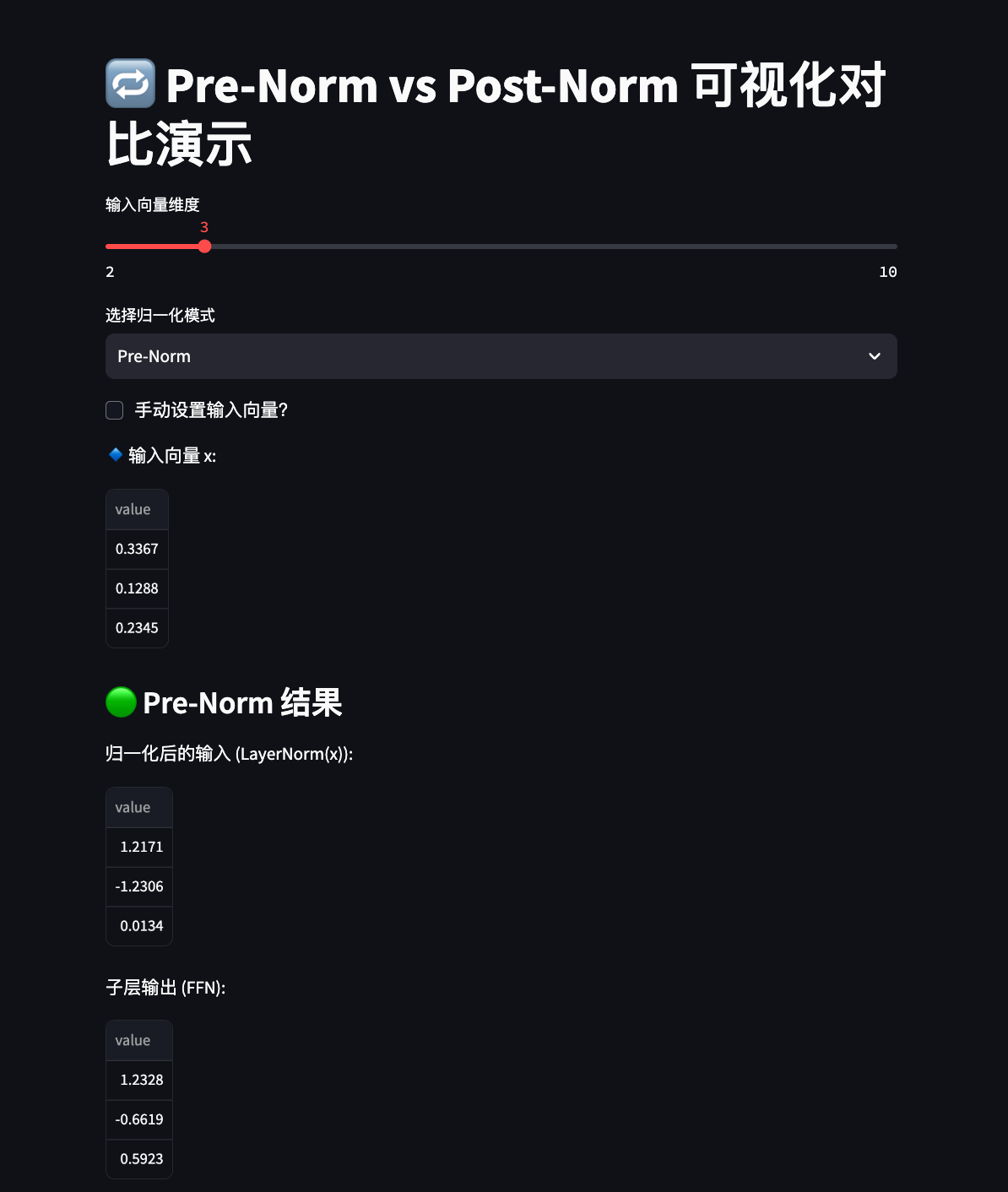
st.title("Pre-Norm vs Post-Norm 可视化对比")
dim = st.slider("输入向量维度", min_value=2, max_value=10, value=4)
mode = st.selectbox("选择归一化模式", ["Pre-Norm", "Post-Norm"])
manual_input = st.checkbox("手动设置输入向量？")

if manual_input:
    x_input = [st.slider(f"维度 {i}", -10.0, 10.0, float(i)) for i in range(dim)]
    x = torch.tensor([x_input], dtype=torch.float32)
else:
    torch.manual_seed(42)
    x = torch.randn(1, dim)

st.write("输入向量 x:", x.numpy().flatten())

if mode == "Pre-Norm":
    model = PreNormBlock(dim)
    x_norm, sub_out, residual = model(x)
    st.subheader("Pre-Norm 结果")
    st.write("归一化后的输入:", x_norm.detach().numpy().flatten())
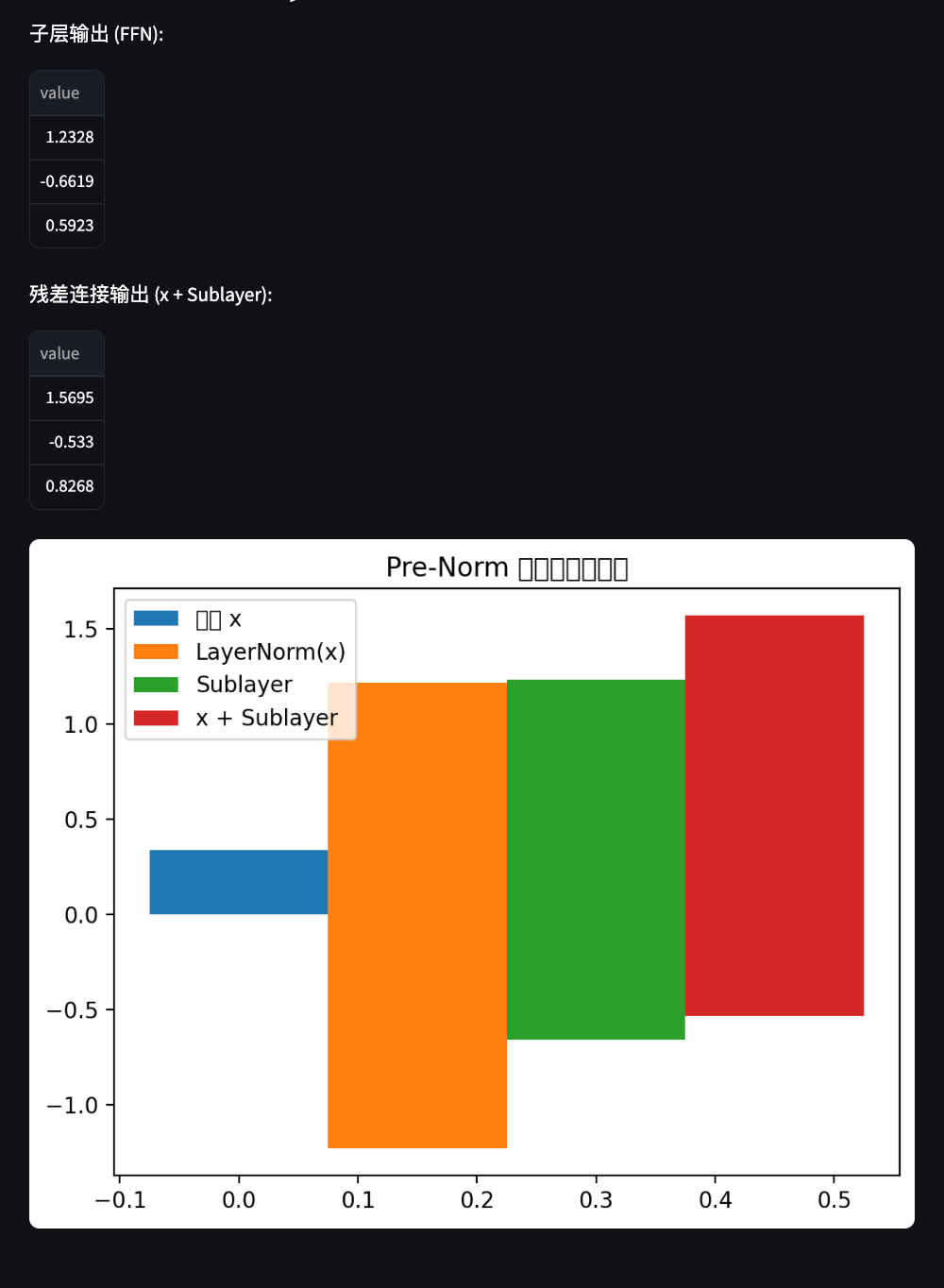
    st.write("子层输出:", sub_out.detach().numpy().flatten())
    st.write("残差连接输出:", residual.detach().numpy().flatten())
else:
    model = PostNormBlock(dim)
    sub_out, residual, out = model(x)
    st.subheader("Post-Norm 结果")
    st.write("子层输出:", sub_out.detach().numpy().flatten())
    st.write("残差连接输出:", residual.detach().numpy().flatten())
    st.write("归一化后输出:", out.detach().numpy().flatten())

def plot_vectors(vectors, labels, title):
    fig, ax = plt.subplots()
    index = np.arange(len(vectors[0]))
    bar_width = 0.15
    for i, vec in enumerate(vectors):
        ax.bar(index + i * bar_width, vec.flatten(), bar_width, label=labels[i])
    ax.set_title(title)
    ax.legend()
    st.pyplot(fig)

if mode == "Pre-Norm":
    plot_vectors(
        [x.numpy(), x_norm.detach().numpy(), sub_out.detach().numpy(), residual.detach().numpy()],
        ["输入 x", "LayerNorm(x)", "Sublayer", "x + Sublayer"],
        "Pre-Norm 各步向量变化"
    )
else:
    plot_vectors(
        [x.numpy(), sub_out.detach().numpy(), residual.detach().numpy(), out.detach().numpy()],
        ["输入 x", "Sublayer", "x + Sublayer", "LayerNorm(x + Sublayer)"],
        "Post-Norm 各步向量变化"
    )

5. 白话版理解残差连接和层归一化

  白话版我们用一个\*\*“写作文 + 编辑润色”的类比\*\*来帮助你直观理解：

🌉 一、残差连接（Residual Connection）= “保留原稿 + 修改建议”

📘 类比场景：

你写了一篇作文（输入 $x$），老师帮你润色修改（变换 $F(x)$），但是老师说：“我不会全改，只在你的原稿上做修改，然后一起返回。”

所以最终交出去的是：

这样做的好处是：

如果老师觉得你写得已经很好（模型学不到更多信息），他可以什么都不改（$F(x) = 0$），直接返回原稿；
如果需要修改，就在原稿上小改，而不是从头重写；
这样作文始终有个保底版本，不会因为老师“瞎改”变得更糟。

👉 这就像神经网络在加深层数时，通过残差连接让输入绕过中间层，始终能保留原始信息，避免“越改越差”。

📏 二、层归一化（Layer Normalization）= “每段话都先统一排版格式”

📘 类比场景：

在你写的每一段文字（样本）中，有些句子特别长，有些特别短，有些特别奇怪。老师（模型）在润色前，会先对每段话做以下操作：

统一行距、字体大小（归一化数值范围）；
调整句式长短，让整体更平衡；
然后再开始修改内容。

这就像是把格式统一再编辑内容，可以让后续工作更顺利。

👉 在神经网络中，不管你输入什么样的特征维度，层归一化都帮你“格式化处理”一下，让训练过程更稳定、更好优化。

🚀 三、在 Transformer 中的使用例子

继续作文类比，Transformer 相当于是一个超级编辑器，里面包含：

注意力机制（找出作文中最重要的句子）；

前馈网络（进行句子重写）；

残差连接（原稿 + 修改）；

层归一化（先格式化文本再修改）；

整个流程是这样的：

原稿 -> 格式标准化（LayerNorm） 
     -> 编辑修改（Attention 或 FFN） 
     -> 保留原稿 + 修改内容（Residual） 
     -> 输出

✅ 总结一句话

概念	类比	本质作用
Residual Connection	老师在你原稿上修改，而不是重写	防止模型“越学越差”，帮助深层网络训练
Layer Normalization	先统一格式，再开始编辑	保证模型每层处理时输入稳定、平衡

6. 总结与工程趋势

残差连接和层归一化是深层神经网络训练稳定性和性能提升的关键。
Pre-Norm 结构已成为现代 Transformer 的主流选择，显著提升了深层模型的可训练性。
工程实现中建议优先采用 Pre-Norm 结构，尤其在大规模模型和长序列任务中。

posted @ 2025-05-12 09:50 何双新阅读(1515) 评论(0) 收藏举报

刷新页面返回顶部

且将新火试新茶

第7讲、残差连接与层归一化：原理、结构与工程实践

1. 残差连接（Residual Connection）

1.1 定义与数学表达

1.2 作用与优势

1.3 工程应用

2. 层归一化（Layer Normalization）

2.1 定义与公式

2.2 作用与适用场景

2.3 与 BatchNorm 对比

3. Transformer 中的归一化与残差结构

3.1 结构对比与演化

3.2 结构图示

3.3 典型架构中的位置说明

3.4 简单代码实现案例

🔵 3.4.1. Post-Norm 实现（原始 Transformer 结构）

🟢 3.4.2. Pre-Norm 实现（现代优化结构）

4. 工程实践与可视化对比

5. 白话版理解残差连接和层归一化

🌉 一、残差连接（Residual Connection）= “保留原稿 + 修改建议”

📘 类比场景：

📏 二、层归一化（Layer Normalization）= “每段话都先统一排版格式”

📘 类比场景：

🚀 三、在 Transformer 中的使用例子

✅ 总结一句话

6. 总结与工程趋势

公告