二叉堆

      二叉堆的本质是一种完全二叉树，它分为两种类型，分别是最大堆和最小堆。

      最大堆的任何一个父节点的值，都大于或者等于它的左右孩子节点的值；最小堆的任何一个父节点的值都小于或等于它的左右孩子结点的值。二叉堆的根结点叫做堆顶。由其性质可以知道，最大堆的堆顶元素是整个堆得最大值，最小堆得的元素是整个堆得最小值。

二叉堆的自我调整

二叉堆的主要操作：

• 插入结点
• 删除节点
• 构建二叉堆

下面以最小堆为例,来看看他的调整过程。

插入节点：

当插入一个节点时，插入的位置是完全二叉树的最后一个位置。例如要插入的新节点为0，为了保持最小堆的特点，新节点0比父节点6小，于是让节点0 做“上浮”操作，与父节点交换位置。后面也是这样依次操作。

 

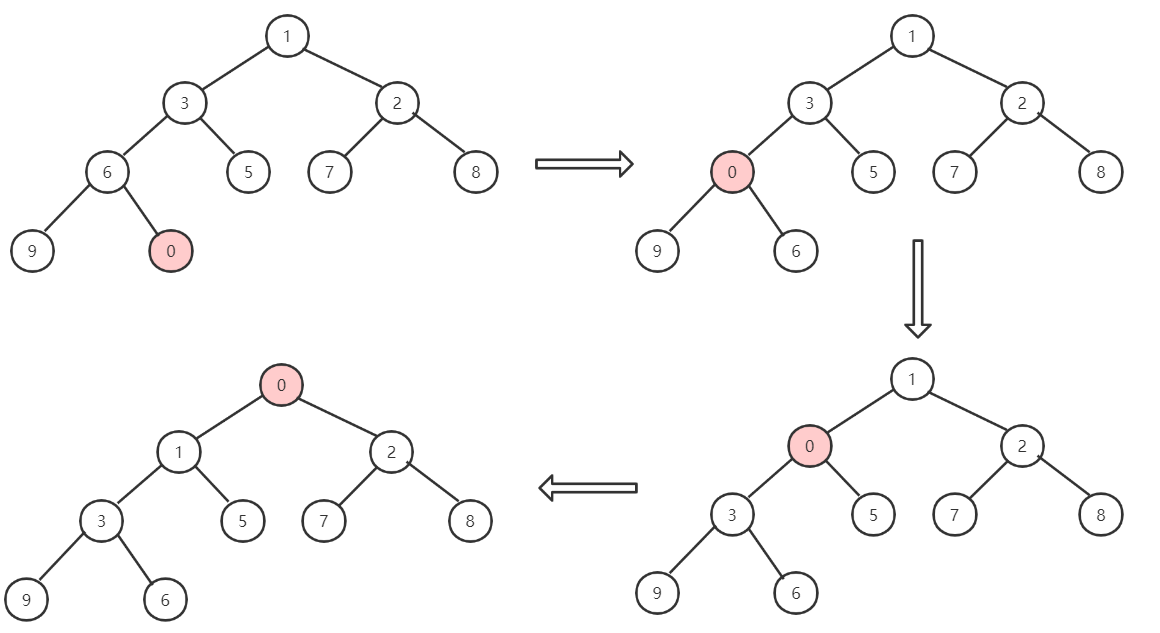
 删除节点：

       二叉堆删除节点的过程与插入节点的过程相反，删除的是堆顶的节点。假如要删除的元素是堆顶的元素1，这时为了保持完全二叉树的结构，此时先将堆的最后一个节点9临时补到原来的堆顶的位置，然后让节点9与其左、右孩子比较，如果左、右孩子节点中的最小的一个（本图是2）节点比其小，就让其 做“下沉” 操作。后面也是这样依次操作。

 

 

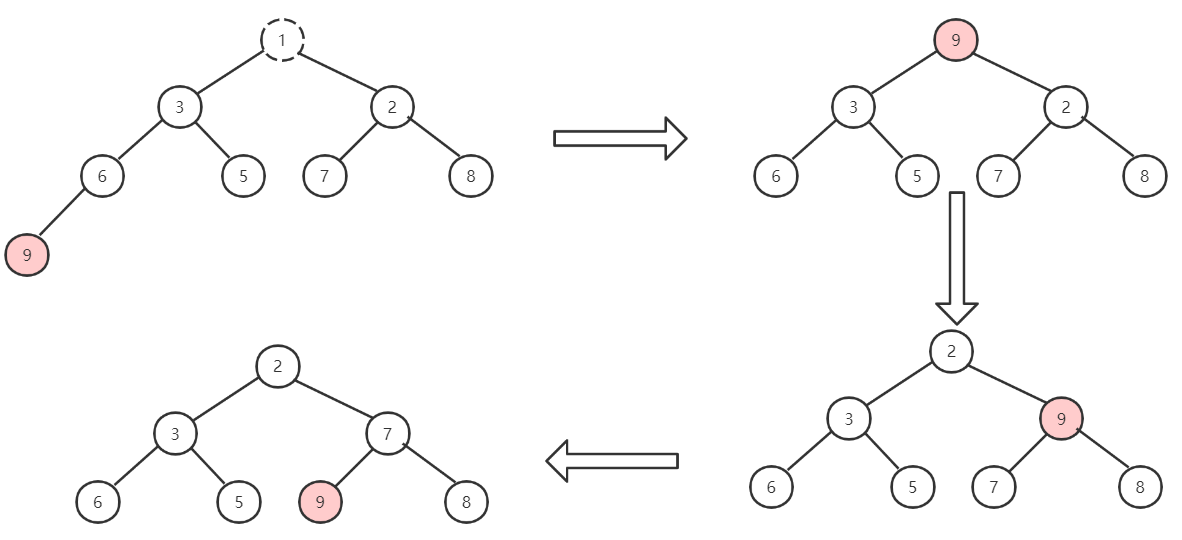
 构建二叉堆

      就是把一个无序的完全二叉树调整为二叉堆，其本质是让所有的非叶子节点依次“下沉”。（首先应该从最后一个非叶子节点开始）

 

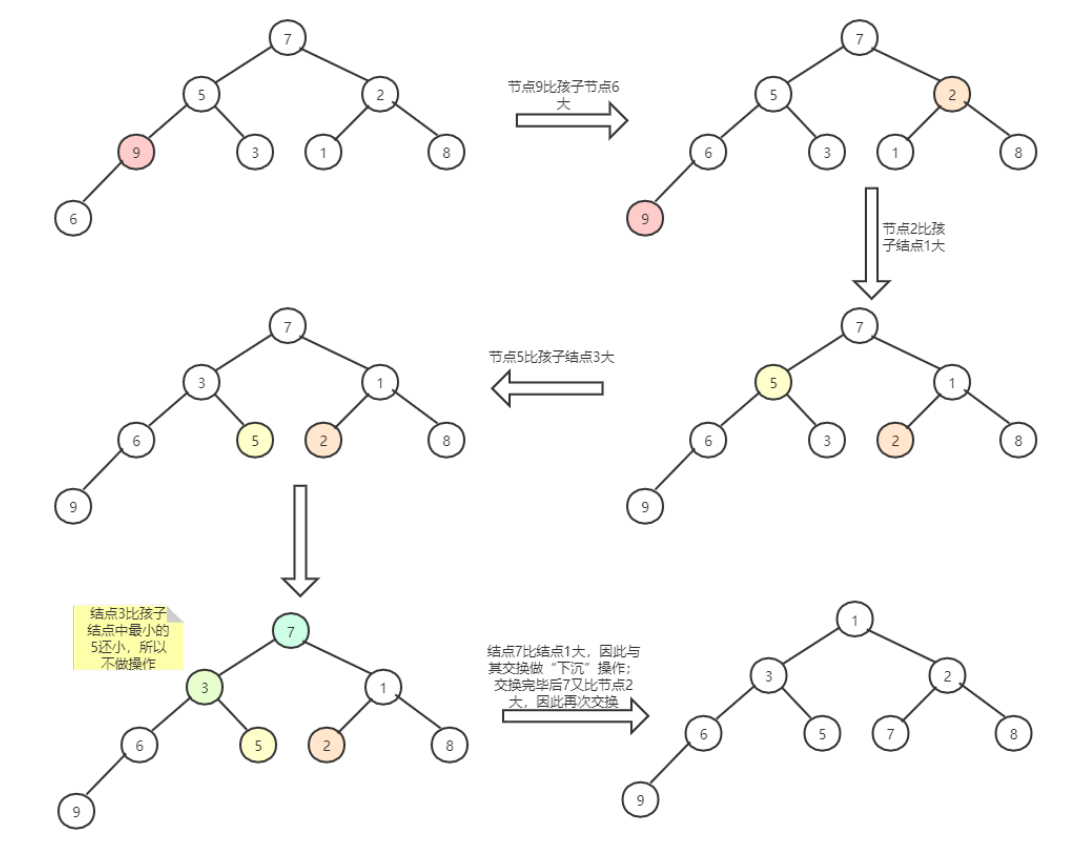
堆得插入或删除都是单一节点的“上浮”或"下沉”操作，这两个操作的平均交换次数都是堆节点数的一半，所以时间复杂度是O(logn)。构建堆得时间复杂度是O(n)。

代码实现（最小堆）：

       二叉堆虽然也是一个完全二叉树，但是他的存储方式确不是链式结构，而是顺序存储。他所有的节点都是存储在数组中的。

 

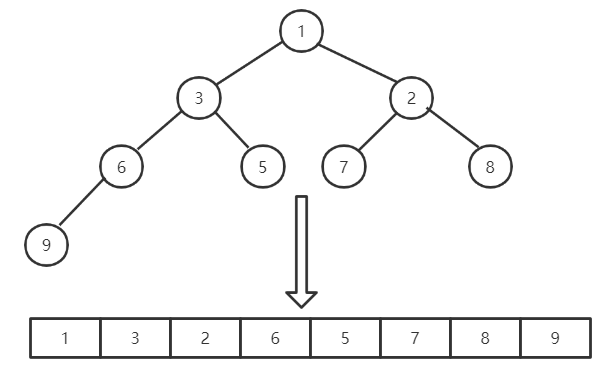
    他的节点确定规则是：令父节点的下标为parent孩子下标为child，则其左孩子下标为parent*2+1，其右孩子下标为parent*2+2。那么如果已知其左孩子下标，则其父节点下标为(child-1)/2。右孩子也是同理。

 /**
     * 上浮调整
     * @param array   待调整的堆
     */
    private static void upAdjust(int[] array) {
        int childIndex = array.length - 1;
        int parentIndex = (childIndex - 1)/2;
        int temp = array[childIndex];   //temp保存插入的叶子结点值，用于最后的赋值
        while (childIndex > 0 && temp < array[parentIndex]){
//            无需真正交换，单向赋值
            array[childIndex] = array[parentIndex];
            childIndex = parentIndex;
            parentIndex = (childIndex - 1)/2;
        }
        array[childIndex] = temp;
    }

    /**
     *构建堆
     * @param array
     */
    private static void buildHeap(int[] array) {

//        从最后一个非叶子结点开始，依次做下沉操作
        for (int i = (array.length - 2)/2; i >= 0 ; i--) {
            downAdjust(array,i,array.length);
        }
    }

    /**
     * 下沉调整
     * @param array  待调整堆
     * @param parentIndex  父节点
     * @param length  数组长队
     */
    private static void downAdjust(int[] array, int parentIndex, int length) {
        //保存父节点值
        int temp = array[parentIndex];
        //左孩子的下标
        int childIndex = 2*parentIndex + 1;
        while (childIndex < length){
            //如果有右孩子并且，右孩子的值比左孩子还小的话，定位到右孩子
            if(childIndex + 1 < length && array[childIndex+1] < array[childIndex] ){
                childIndex++;
            }
            if(temp <= array[childIndex])
                break;  //父节点小于任意一个子节点
                array[parentIndex] = array[childIndex];
                parentIndex = childIndex;
                childIndex = 2*parentIndex + 1;
        }
        array[parentIndex] = temp;

    }

 最大堆只需要在上面基础上进行稍微的改动即可。