P6619 [省选联考 2020 A/B 卷] 冰火战士

P6619 [省选联考 2020 A/B 卷] 冰火战士

不得不说这题除了不会树状数组上倍增其他应该不难想。

分析题目，设场上温度为 \(t\)，那么上场的战士要求 \(t_{fire}\ge t,t_{ice}\le t\)，且注意到答案为上场的冰战士和火战士各能量之和的较小值的两倍。我们令 \(f(x)\) 为当温度在 \([1,x]\) 时能够出战的冰战士的能量之和，令 \(g(x)\) 为当温度在 \([x,maxv]\) 时能够出战的火战士的能量之和，不难看出 \(f(x)\) 为冰战士按温度升序后的前缀和，而 \(g(x)\) 为火战士按温度升序的后缀和，所以 \(f(x)\) 单调递增，\(g(x)\) 单调递减。二者的图像如下图所示：

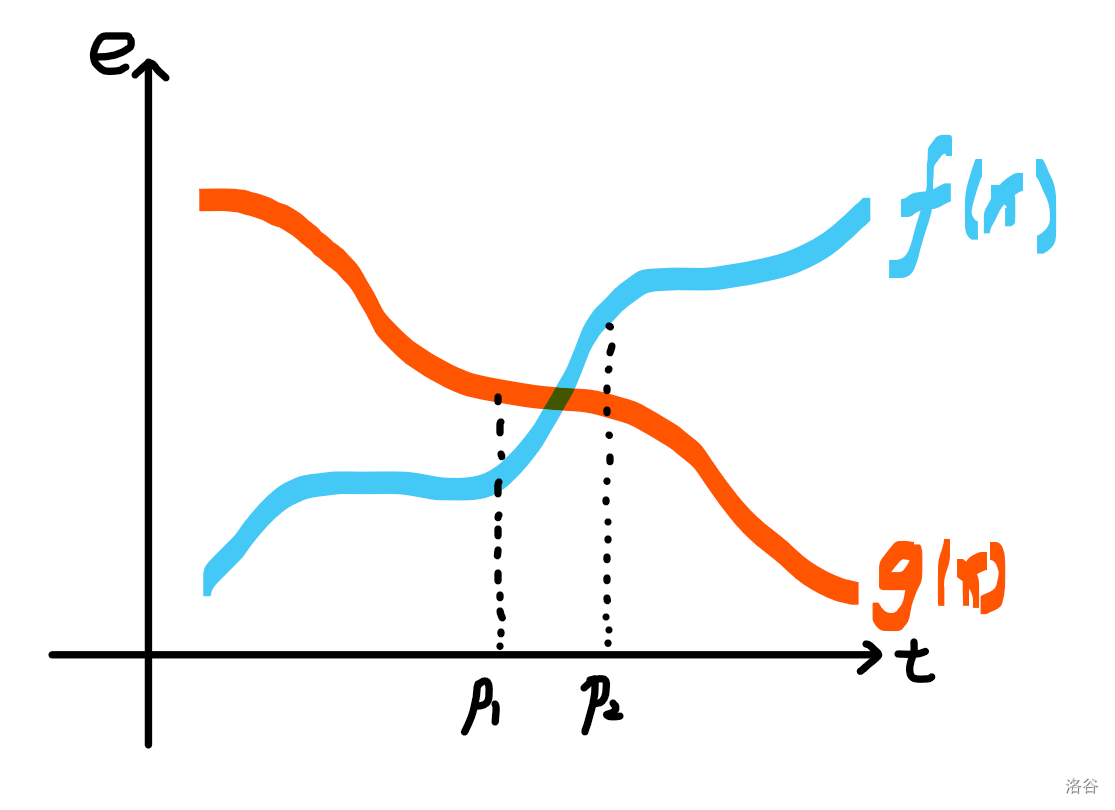
我们要求的是 \(2\min(f(x),g(x))\)，这个值当取到交点时最大（当然也有没有交点的情况），但是函数并非是连续的，但是可以二分找到交点左右两边最近的两个点，于是我们就得到一个不错的算法：

1. 先将温度离散化，利用树状数组维护前缀和以及后缀和。

2. 二分找到一个最大的 \(p_1\) 满足 \(f(p_1)<g(p_1)\)。那么一定有 \(f(p_1+1)\ge g(p_1+1)\)，再二分找到最大的 \(p_2\) 满足 \(g(p_2)=g(g_1+1)\)。

二分套了树状数组查询，时间复杂度为 \(O(n\log^2n)\)，代码是可以过的。

考虑进一步优化，利用树状数组上倍增，可以将复杂度优化到 \(O(n\log n)\)。

代码：

#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;

inline int read() {
	int x = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
	while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
	return x*f;
}

inline void write(int x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x/10);
	putchar('0'+x%10);
}

const int N = 2e6+5;
struct que { int op, t, x, y; } a[N];
int q, n, idx, sum, b[N];

struct bit {
	int c[N];
	inline void add(int x, int k) { for (; x <= n; x += x&-x) c[x] += k; }
	inline int ask(int x) { int res = 0; for (; x; x -= x&-x) res += c[x]; return res; }
} t[2];

int main() {
	q = read();
	for (int i = 1; i <= q; ++i) {
		a[i].op = read(), a[i].t = read();
		if (a[i].op == 1) a[i].x = read(), a[i].y = read(), b[++idx] = a[i].x;
	}
	sort(b+1, b+idx+1);
	n = unique(b+1, b+idx+1)-b-1;
	for (int i = 1; i <= q; ++i) if (a[i].x) a[i].x = lower_bound(b+1, b+n+1, a[i].x)-b;
	for (int i = 1; i <= q; ++i) {
		if (a[i].op == 1) {
			if (a[i].t) t[1].add(a[i].x+1, a[i].y), sum += a[i].y;
			else t[0].add(a[i].x, a[i].y);
		}
		else {
			int k = a[i].t;
			if (a[k].t) t[1].add(a[k].x+1, -a[k].y), sum -= a[k].y;
			else t[0].add(a[k].x, -a[k].y);
		}
		int p1 = 0, p2 = 0, s0 = 0, s1 = sum, m1 = 0, m2 = 0;
		for (int j = 20; ~j; --j) {
			if (p1+(1<<j) > n) continue;
			int x = s0+t[0].c[p1+(1<<j)], y = s1-t[1].c[p1+(1<<j)];
			if (x < y) p1 += 1<<j, s0 = x, s1 = y;
		}
		m1 = s0, s0 = 0, s1 = sum;
		if (p1 < n) {
			m2 = min(t[0].ask(p1+1), sum-t[1].ask(p1+1));
			for (int j = 20; ~j; --j) {
				if (p2+(1<<j) > n) continue;
				int x = s0+t[0].c[p2+(1<<j)], y = s1-t[1].c[p2+(1<<j)];
				if (x < y || min(x, y) == m2) p2 += 1<<j, s0 = x, s1 = y;
			}
		}
		if (!max(m1, m2)) puts("Peace");
		else write(b[m2 >= m1 ? p2 : p1]), space, write(2*max(m1, m2)), enter;
	}
	return 0;
}