题解：P12550 [UOI 2025] Reversal ABC

提供一种不一样的思路，也是 \(O(n)\) 的，不需要复杂 DP。

首先注意到几个结论：

• 注意到一个元素只会往一个方向移动。

• 注意到如果同一个元素最多只会用一种方式移动，比如对于一个 A，如果用 AB -> BA 交换过了，就不可能再通过 CA -> AC 再交换，以后都只能用 AB -> BA 了。

• 注意到可以先把在一起的相同元素缩在一起，交换时在一起的相同元素只会往一边交换。

• 注意到以上结论我想了 1 个小时。

接下来考虑建图，在移动起点和移动终点间连一条线段，权值为操作次数。

比如 CABC，可以建出如下图：

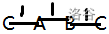
此时答案为选择两两不重叠的线段时的最大权值和（点重叠也算重叠，例子中答案就是选 CA 线段和 BC 线段）。这个直接随便 DP 即可。设 \(f_i\) 表示从 \(1\sim i\) 的最大权值，直接 \(f_i\gets\max(f_{i-1},\max_{(j,i,w)\text{ is a segment}}\{f_{j-1}+w\})\)，注意一下我在的代码中是反着 DP 的。

但实际上它不一定是相邻的交换，还有一大堆漏洞。例如 CABABABC，此时第一个 A 可以连向这段区间后面所有的 B，是 \(O(n^2)\) 的。同时，中间的 A 本来也可以和 B 交换，但因为不能选重叠线段就没了。

对于上述问题，可以视为都是 ABABABAB 型导致的（BCBCBC 和 CACACA 同理下面就不说了），逐一修复：

• “因为不能选重叠线段就没了”，考虑把中间的贡献也带着计算上。例如第一个 A 和第二个 B 连边时权值就变成 \(3\) 而非 \(2\)。
• “关于时间复杂度和边数 \(O(n^2)\)”，考虑再注意到一个结论。

  • 此时只有第一个 A 和最后一个 B 有可能被两边的字符带着交换导致不参与这个大段（例如 CACACACACAC[A BABA B]CBCBCBCBCBCBC），但中间的绝对会交换。

  • 所以只建第一个 A 到最后一个 B、第二个 A 到最后一个 B、第一个 A 到倒数第二个 B、第二个 A 到倒数第二个 B 的边即可。对应边的贡献贡献直接减减少量即可。效果如下图所示：

  • 

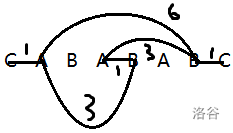
  • 此时可以直接扫过去计算，所以时间复杂度也跟着变成 \(O(n)\) 的了。

代码：（有亿点丑，不建议看）

#include<bits/stdc++.h>
using namespace std;
namespace estidi{
	const int mn=1000003;
	struct num{
		int tp;
		long long cnt;
	};
	char cc[mn];
	long long f[mn];
	vector<num>v,nv[mn];
	int main(){
		int tc,n,pre;
		long long cnt;
		string s;
		scanf("%d",&tc);
		while(tc--){
			scanf("%d %s",&n,cc);
			s=cc;
			pre=s[0]-'A'+1;
			cnt=0;
			v.push_back({0,0});
			for(int i=0;i<n;i++){
				if(s[i]-'A'+1!=pre){
					v.push_back({pre,cnt});
					pre=s[i]-'A'+1;
					cnt=0;
				}
				cnt++;
			}
			v.push_back({pre,cnt});
			v.push_back({0,0});
			for(int i=1;i<v.size()-1;i++)
				if(v[i+1].tp==(v[i].tp%3+1)){
					int pos=i;
					long long now=0,anow=0,ans=0;
					while(v[pos].tp==v[i].tp&&v[pos+1].tp==v[i+1].tp){
						now+=v[pos].cnt;
						anow+=v[pos+1].cnt;
						ans+=now*v[pos+1].cnt;
						pos+=2;
					}
					pos-=2;
					if(i==pos)
						nv[i].push_back({i+1,ans});
					else
						if(i==pos+2){
							nv[i].push_back({pos+1,ans});
							nv[i].push_back({pos-1,ans-now*v[pos+1].cnt});
							nv[i+2].push_back({pos+1,ans-anow*v[i].cnt});
						}
						else{
							nv[i].push_back({pos+1,ans});
							nv[i].push_back({pos-1,ans-now*v[pos+1].cnt});
							nv[i+2].push_back({pos+1,ans-anow*v[i].cnt});
							nv[i+2].push_back({pos-1,ans-anow*v[i].cnt-now*v[pos+1].cnt+v[i].cnt*v[pos+1].cnt});
						}
					i=pos;
				}
			for(int i=1;i<v.size();i++){
				f[i]=max(f[i],f[i-1]);
				for(int j=0;j<nv[i].size();j++){
					f[nv[i][j].tp+1]=max(f[nv[i][j].tp+1],f[i]+nv[i][j].cnt);
				}
			}
			printf("%lld\n",f[v.size()-1]);
			for(int i=1;i<v.size();i++){
				vector<num>().swap(nv[i]);
				f[i]=0;
			}
			vector<num>().swap(v);
		}
		return 0;
	}
}
int main(){
	// freopen("string.in","r",stdin);
	// freopen("string.out","w",stdout);
	estidi::main();
	return 0;
}