AT_arc153_b [ARC153B] Grid Rotations 题解

很久以前打第一场 ARC 时的 B 题，现在差点都还没做出来……

不会写平衡树，因此考虑其它做法。

观察样例二，发现答案好似就是把串往下和往右滚动了几下。

再想一下，发现每两次旋转都可以视为滚动，考虑两次两次计算贡献，如果是奇数次最后一次单独处理。

假设每一个数代表一小块，那么滚动好像是这样的（由于内部旋转了也要旋转回来，就不画了）：

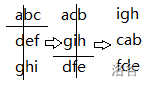
但是分析样例发现假如直接按照它下标来划分块会出问题，会被切断。

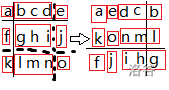
发现分段应该推出第二根分割线在第一根之前的位置，再划分：

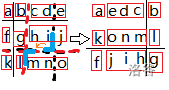
显然，滚动可以先不看字符，最后直接加上偏移量，然后就做完了。

虽然说着简单，实际上旋转后坐标推着和写着很麻烦，写了 2 个小时！（因此到了考场还是做不出来……）

代码下标有时候是从 0 开始的，因此很屎。

#include<bits/stdc++.h>
using namespace std;
namespace estidi{
	string s[500003];
	int main(){
		int h,w,q,x,y,xx,yy;
		long long rr=0,dr=0;
		scanf("%d%d",&h,&w);
		for(int i=0;i<h;i++)
			cin>>s[i];
		scanf("%d",&q);
		for(int i=2;i<=q;i+=2){
			scanf("%d%d%d%d",&x,&y,&xx,&yy);
			x--;
			y--;
			xx--;
			yy--;
			if(xx<=x)
				xx=x-xx;
			else
				xx=h-xx+x;
			if(yy<=y)
				yy=y-yy;
			else
				yy=w-yy+y;
//			cerr<<xx<<" "<<yy<<endl;
//			cerr<<x<<" "<<y<<endl;
			dr+=h-xx;
			rr+=w-yy;
//			cerr<<dr<<" "<<rr<<endl;
		}
		dr=(dr%h+h)%h;
		rr=(rr%w+w)%w;
		if(q%2==1){
			scanf("%d%d",&x,&y);
			x--;
			y--;
			for(int i=0;i<h;i++){
				for(int j=0;j<w;j++){
					int nx,ny;
					if(i<=x)
						nx=x-i;
					else
						nx=h-i+x;
					if(j<=y)
						ny=y-j;
					else
						ny=w-j+y;
//					cerr<<i<<" "<<j<<" "<<nx<<" "<<ny<<" "<<dr<<" "<<rr<<" "<<s[nx][ny]<<endl;
					printf("%c",s[(nx-dr+h)%h][(ny-rr+w)%w]);
				}
				printf("\n");
			}
		}
		else{
			for(int i=0;i<h;i++){
				for(int j=0;j<w;j++)
					printf("%c",s[(i-dr+h)%h][(j-rr+w)%w]);
				printf("\n");
			}
		}
		return 0;
	}
}
int main(){
	estidi::main();
	return 0;
}